This site is being phased out.
Test
Applied Topology and Geometry by Peter Saveliev
This is a book draft, in progress. I would appreciate your comments. If you are a beginner, you might want to start here instead.
For a book reading experience, ignore the links in the articles. Instead, click Back when you are finished.
Contents
- 1 Introduction
- 2 Homology of graphs
- 3 Analysis of digital images
- 4 Continuous differential forms
- 5 Cubical differential forms
- 6 Integration of differential forms
- 7 Cohomology
- 8 From vector calculus to exterior calculus
- 9 Point-set topology
- 10 New spaces from old
- 11 Manifolds and differential forms
- 12 Cubical homology
- 13 Geometry and differential forms
- 14 Cell complexes
- 15 Simplicial complexes
- 16 Homology and cohomology
- 17 Homology and computations
- 18 Maps and their homology
- 19 More on maps
- 20 Properties of homology groups
- 21 Differential geometry
- 22 Physics modelling with discrete PDEs
- 23 Parametrized complexes and robustness of topology
- 24 Equilibria and reachability
- 25 PageRank: how not to do things
- 26 Examples of spaces
- 27 Exercise sets
- 28 References
Introduction
A sample of the ideas that the text follows -- in broad brushstrokes.
- Topology vs algebra vs geometry
- Topology in real life
- Equivalence of topological features: homology
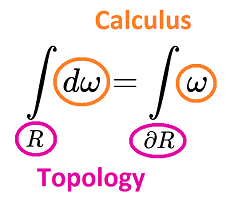
- Homology in Calculus
- A modern view of calculus: differential forms
- Is topology enough?
Homology of graphs
The best place to get started with homology theory is graphs. One only needs to be concerned with two topological features: components and holes.
Analysis of digital images
With a very little background one can make a good progress in this very important area. Many ideas reappear later -- on a more advanced level.
- Zooming in beyond the pixels: cell decomposition of images
- Space decomposed into little pieces: cubical complexes (*)
- The topology of a binary image
- The topology a gray scale image
- The geometry a gray scale image
- Lengths of digital curves
Continuous differential forms
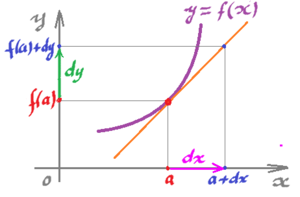
An introduction, starting with what you've seen in Calculus: $1$-forms.
- Differentials
- Examples of differential forms
- Algebra of differential forms
- Continuous functions (*)
- Wedge product of continuous forms
- Exterior derivative
- Properties of the exterior derivative
Cubical differential forms
Roughly, they are constant on each cell of a cubical complex. They are "discrete" in this sense. We don't establish a direct relation to the continuous forms yet just observe that they behave similarly.
- Space decomposed into little pieces: cubical complexes (*)
- Discrete differential forms
- Algebra of discrete differential forms
- Chains vs cochains
- Calculus of discrete differential forms
Integration of differential forms
The main goal is to develop analogues of the integral theorems of vector calculus (Gauss, Green, etc). In terms of the exterior derivative, they finally make sense as a whole!
- Inside vs outside: orientation
- Integration of differential forms of degree 0 and 1
- Orientation of manifolds
- Integral theorems of vector calculus
- Integration of differential forms of degree 2
- Properties of integrals of differential forms
- The best one: General Stokes Theorem
- Linear algebra in elementary calculus
- Continuous vs discrete differential forms
Cohomology
From the calculus of differential forms, continuous or discrete, one can derive the topology of the underlying space.
- Calculus and algebra vs topology
- Closed and exact forms
- Path-connectedness (*)
- Continuously deforming continuous functions: homotopy (*)
- Closedness and exactness of 1-forms
- Quotients of vector spaces (*)
- de Rham cohomology
- Tunnels
- Change of variables for differential forms
- Cochain complexes and cohomology
- Cohomology of figure 8
From vector calculus to exterior calculus
The correspondence between calculus of functions and vector fields in dimensions $2$ and $3$ on one hand and that of differential forms of various degrees on the other is revealed. The correspondence between $grad, div, curl$ and the exterior derivatives of appropriate degrees shows the advantage of the latter approach.
- Fundamental correspondence
- Identities of vector calculus
- Cross and dot products of vector fields under fundamental correspondence
- Modelling motion with discrete forms
Point-set topology
We need more background for our study. The main topic is continuity, in the setting of $n$-dimensional Euclidean spaces.
- Topology in calculus
- Topology with points and sets only
- Neighborhoods and topologies
- Open and closed sets
- Classification of points with respect to a subset
- Continuous functions (*)
- Path-connectedness (*)
- Topological equivalence: homeomorphisms
- Compactness
- Separation axioms
New spaces from old
Tools for building the topological complexity that we'll need...
- Gluing things together: quotient spaces
- Quotients of manifolds
- Connected sum
- Subspaces: relative topology
- Product topology
- Examples of maps
Manifolds and differential forms
Calculus on manifolds is a necessity; ask Einstein!
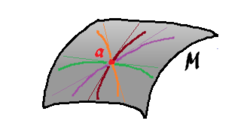
- Manifolds model a curved universe
- More about manifolds
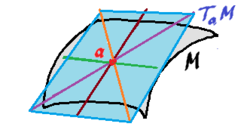
- Tangent bundle
- Tangent bundles and differential forms
- Cubical tangent bundle
- Modelling motion on manifolds
- Configuration spaces
Cubical homology
The relation between cells and their boundaries reveals the topology of the space. Little algebra, for now.
- The count of topological features: Betti numbers
- Space decomposed into little pieces: cubical complexes (*)
- Boundary operator of cubical complex
- All cells and all boundaries in one place: Cubical chain complex
- Quotients of vector spaces (*)
- Homology of cubical complexes
- Examples of homology of cubical complexes
- Realizations of cubical complexes
Geometry and differential forms
Topology: everything is deformable. Geometry: also keep track of size. Adding an extra structure to our manifolds allows us to measure things: distances and angles, and then lengths, curvatures, areas, volumes, etc.
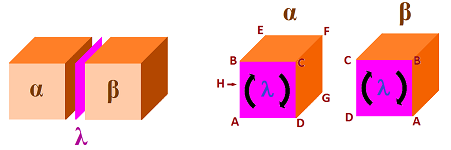
Cell complexes
Going beyond simply decomposing the Euclidean space into squares and cubes. We can build anything from little pieces -- in vacuum!
- Products of complexes
- Cell complexes
- Blueprint of complex: Skeleton
- Examples of cell complexes
- Gluing boundary to boundary: Quotients of complexes
- Count vertices, edges, and faces: Euler characteristic
- Down in dimension: Boundary operator
Simplicial complexes
Turning the relation between cells and their boundaries into algebra.
- From squares to triangles: Simplicial complexes
- Euler characteristic of graphs
- Surfaces
- Triangulations of surfaces
- Orientable surfaces
- Euler characteristic of surfaces
- Abstract simplicial complexes
- Approximate topological spaces: Nerve of cover
- Boundary operator of simplicial complexes
Homology and cohomology
The algebra of the chains and boundaries reveals the topology of the space. And so does the algebra of the cochains and coboundaries. Progressing from cubical complexes to cell complexes.
- The algebra of chains
- Homology of cubical complexes
- Homology and algebra
- Homology as a vector space
- Holes and tunnels: Homology in dimension 1
- Voids: Homology in dimension 2
- Homology of balls and spheres
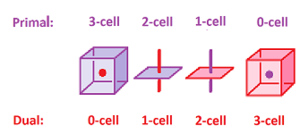
- Dual spaces
- Cohomology
Homology and computations
The computability of the homology of cell complexes is what makes applications possible.
- Examples of homology of cubical complexes
- How to compute Betti numbers
- How to compute homology
- Point clouds and simplicial complexes: Vietoris-Rips complex
- Point clouds and simplicial complexes: Delauney triangulation
- Robustness of topology: persistence
Maps and their homology
Continuous functions also have algebraic interpretations via homology -- as linear operators.
- Homology classes under maps
- Commutative diagrams
- Cell to cell: cell maps
- Boundary to boundary: chain operators
- Homology class to homology class: homology operators
- Persistence via homology operators
More on maps
The topology of continuous functions.
- Continuously deforming continuous functions: homotopy (*)
- Simple connectedness (*)
- Homology of homotopic maps
- Simplex to simplex: Simplicial maps
- Compositions of simplicial maps
- Derivative to derivative: cochain operators
- Homology and cohomology operators
- Homotopy equivalence
- Fundamental group
- Motion planning in robotics
Properties of homology groups
Progressing from homology as a vector space to groups. Building the rest of the theory... From now on, "homology" means "homology and cohomology".
- Homology as a group
- Properties of homology groups
- Homology of surfaces
- Betti numbers vs Euler characteristic: Euler-Poincare formula
- Spaces vs subspaces: relative homology
- Exact sequences
- Homology vs homology of the complement: Alexander duality
- Homology vs cohomology in manifolds: Poincare duality
- Homology of the product: Kunneth formula
- Isomorphic homology: Vietoris Mapping Theorem
- Cup product and cap product
Differential geometry
With the metric tensor we can measure lengths, curvatures, areas, volumes, etc.
- Riemannian manifolds
- Codifferential
- The Laplacian
- Hodge decomposition
- Gauss-Bonnet theorem
- Poincare-Hopf index theorem
- Ranking movies with discrete differential forms
- Voting and the Arrow's Impossibility Theorem
Physics modelling with discrete PDEs
Normally, one uses partial differential equations, i.e., equations with respect to derivatives of the quantities involved, and then "discretizes" these PDEs via finite differences to create a simulation. Instead, we look at the derivations of these PDEs and, based on the physics, represent each quantity as a differential form of an appropriate degree. The discrete versions of these equations, i.e., equations with respect to discrete differential forms, are ready-made simulations of the processes. The main advantage of this bottom-up approach is that the laws of physics (conservation of energy, conservation of mass, etc) are satisfied exactly rather than approximately.
- Wave equation
- Navier–Stokes equations for fluid flow
- Heat transfer
- Maxwell equations of electromagnetism
- Wave equation from Maxwell equations
- Thermodynamics
- Black–Scholes derivatives pricing
- Cellular automata
Parametrized complexes and robustness of topology
In real life, the data comes from an environment where numerous parameters interact with each other. It is a special challenge to extract topology from such data. In addition, the data comes with noise and other uncertainly. Therefore, the topological features we've found aren't created equal and have to be filtered to reveal the true reality underneath.
- Parametrized complexes
- The homology of a gray scale image
- Homology groups of filtrations
- Robustness of topology
- The high contrast homology of a gray scale image
- Persistent homology groups of filtrations
- Computing persistent homology of filtrations
- The topology of a color image
- Multiparameter filtrations
Equilibria and reachability
Its homology map might detect whether a map has to have a fixed point, $f(x)=x$. This concept corresponds to that of equilibrium for dynamical systems. Another correspondence exists between surjectivity of maps and reachability of control systems.
- Brouwer fixed point theorem
- Degree of map
- Equilibria of dynamical systems
- Lefschetz number and fixed points of maps
- Set-valued maps
- Fiber bundles
- Lefschetz theory for coincidences
- Lefschetz numbers in control theory
PageRank: how not to do things
A positive business lesson, but a negative mathematics lesson (Columbus' estimate of the size of the Earth is another example). To appreciate the difference, read the rest of the book.
- What is PageRank?
- PageRank's dependence on the damping factor
- PageRank as a probability distribution
- PageRank as a solution of a matrix equation
- PageRank: testing
- PageRank as a flow: how to do things
Examples of spaces
This part is intended as a quick reference.
Exercise sets
- Differential forms: exams
- Differential forms: review questions
- Introductory algebraic topology: review exercises
- Topology II -- final exam
- Topology II -- midterm
References
- Topology of Surfaces by Kinsey
- Basic Topology by Armstrong
- Introduction to Topology by Gamelin and Greene
- Computational Homology by Kaczynski, Mischaikow, Mrozek
- Topology for Computing by Zomorodian
- Computational Topology by Edelsbrunner and Harer
- Introduction to Topology: Pure and Applied by Adams and Franzosa
- Differential Forms: A Complement to Vector Calculus by Weintraub
- Applied Differential Geometry by Burke
- From Calculus to Cohomology by Madsen
- Discrete Calculus: Applied Analysis on Graphs for Computational Science by Grady and Polimeni
- Mimetic Discretization Methods by Castillo
- A New Kind of Science by Wolfram
Note: sections marked with (*) appear more than once.
College Algebra -- Fall 2014 -- final exam
Name:_________________________ $\qquad$ 12 problems, 10 points each
- Justify every step you make with as thorough an explanation as possible, in English.
- Unless requested, no decimal representation of the answers is necessary.
- Start every problem at the top of the page.
$\bullet$ 1.
$$\begin{array}{lll}
\\
\\
\\
\\
\\
\\
\\
\\
\\
\\
\\
\\
\\
\\
\\
\\
\\
\\
\\
\\
\\
\\
\\
\\
\\
\\
\hline
\end{array}$$