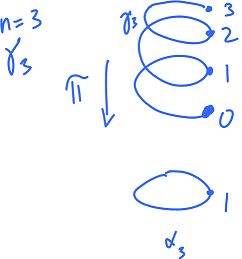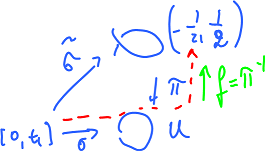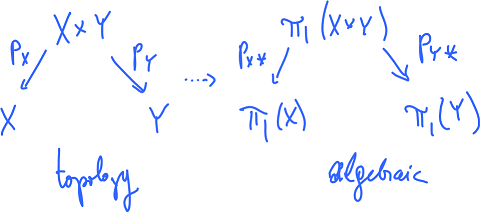This site is being phased out.
Fundamental group
Let $(X,x_{0})$ be a pointed topological space, i.e., a topological space with a chosen point $x_{0}$, called the basepoint.
The fundamental group of $(X,x_0)$, $\pi _1(X,x_{0})$, is the group of loops based at $x_{0}$, up to a based homotopy. We define a product on this group by $$<\sigma> \cdot <\tau>=<\sigma \cdot \tau >,$$ where $<x>$ stands for the homotopy class of $x$ and $\sigma \cdot \tau$ means "travel along $\sigma$ and then $\tau$".
Everything starts with this main theorem:
Theorem. $$\pi_1({\bf S}^1)={\bf Z}.$$
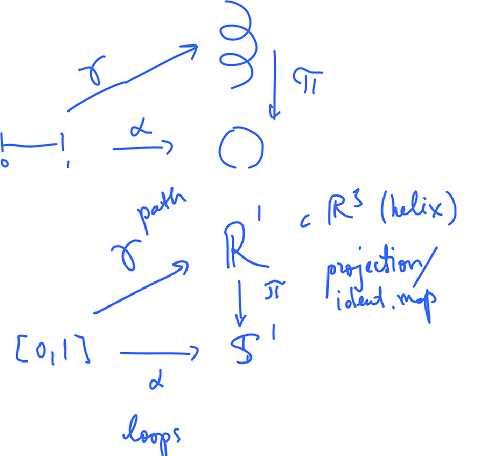
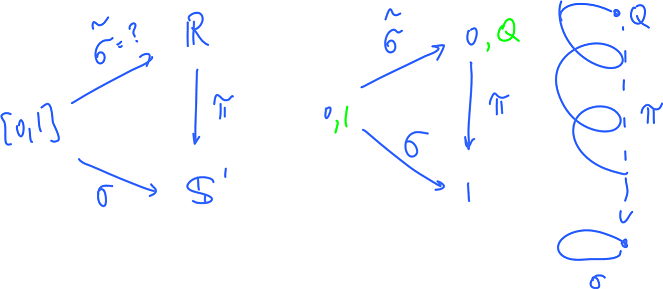
Proof. The idea of the proof is to "lift" the loops in the circle to the ones in the real line:
Here, if one thinks of the circle as a subset of the complex plane, the projection is given by $\pi (x)=e^{2\pi ix}$.
In particular, the standard $n$-times wrapping loop $\alpha _n$ of the circle is lifted to $\gamma_n$ given by $\gamma_n(s)=ns$: $$\alpha_n=\pi\gamma_n.$$
Then the homomorphism $$\phi:\pi_1({\bf S}^1) \leftarrow {\bf Z}$$ is defined by $$\phi(n)=<\alpha_n>.$$ To prove that this is indeed a homomorphism, we need to show that $$\phi(n+m)=\phi(n)\cdot\phi(m),$$ or $$<\alpha_{n+m}>=<\alpha_n>\cdot<\alpha_m>.$$ We need to connect $\gamma_{n+m}$ with $\gamma_n,\gamma_m$:
We define the shift $$\sigma=\gamma_n+m,$$ then $$\pi\sigma=\pi\gamma_n.$$ Therefore $$\phi(n+m)=^{def}=<\alpha_{n+m}>=<\pi\gamma_{n+m}>.$$ Since $\gamma_{n+m}=\sigma\cdot\gamma_m$, this is equal to $$=<\pi(\sigma\cdot\gamma_m)>.$$ Since homotopies are preserved under compositions, this is $$=<(\pi\sigma)\cdot(\pi\gamma_m)>$$ $$=<(\pi\gamma_n)\cdot(\pi\gamma_m)>.$$
Now, how do we construct $\gamma$ from an arbitrary $\alpha$ so that $\pi\gamma=\alpha$? Piece by piece.
The inverse of $\pi$ doesn't exist but locally -- on "small" pieces -- it does.
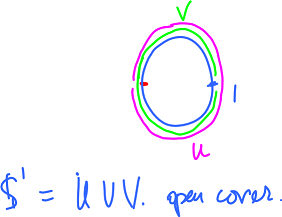
So, we start with an open cover of the circle of, say, two elements:
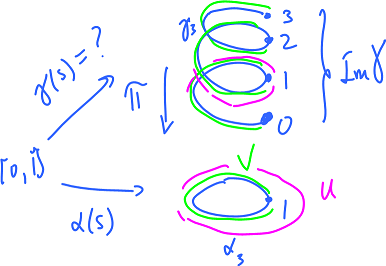
We now lift it.
We have 3 pieces of $\pi^{-1}(V)$, call them $V_1,V_2,V_3$. Then, restricted to any of these, $\pi$ is a homeomorphism.
Now we define $$\gamma(s)=\pi^{-1}(\alpha(s))$$ if $\alpha(s) \in V_i$ picking the corresponding inverse of each of these sets. Suppose, for example, that we have
- the first loop of $\alpha$ defined on $(0,1/3)$, then we pick $\pi^{-1}$ defined on $V_1$;
- the second loop of $\alpha$ defined on $(1/3,2/3)$, then we pick $\pi^{-1}$ defined on $V_2$;
- the first loop of $\alpha$ defined on $(2/3,1)$, then we pick $\pi^{-1}$ defined on $V_3$.
If there seems to be a gap in transition, it's taken care of by $U$, in a similar fashion. Then we have $\gamma$ defined separately on: $$V_1,U_1,V_2,U_2,V_3,U_3.$$ Since the values match on the overlaps, $\gamma$ is well defined.
The surjectivity of $\phi$ follows from the following lemma.
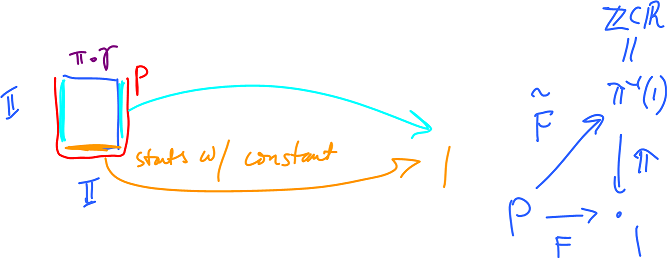
Path-Lifting Lemma. Suppose $\sigma$ is a path in ${\bf S}^1$ that starts at $1$. Then there is a unique path $\tilde{\sigma}$ in ${\bf R}$ which begins at $0$ and satisfies: $$\pi\tilde{\sigma}=\sigma.$$
Proof. We have a map $$\sigma:[0,1] \to {\bf S}^1.$$ we now need to build $$\tilde{\sigma}:[0,1] \to {\bf R}.$$
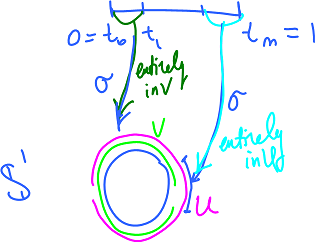
Suppose $\{U,V\}$ is this open cover of ${\bf S}^1$: $$U={\bf S}^1-\{0\},V={\bf S}^1-\{1\}.$$ Then $$T=\{\sigma^{-1}(U),\sigma^{-1}(V)\}$$ is an open cover of $[0,1]$. These sets may be disconnected. We need connected set, i.e., intervals, to build $\tilde{\sigma}$ step by step. Fortunately, we know that an open in ${\bf R}$ is the disjoint union of intervals.
We use Lebesgue Lemma:
- there is $d>0$ such that every set of diameter $<d$ will be contained in either $\sigma^{-1}(U)$ or $\sigma^{-1}(V).$
Let's cut $[0,1]$ into intervals. We let $$m=[1/d]+1$$ to guarantee that $$t_{i+1}-t_i<d,$$ so let $$t_i=i/m.$$ The choice of $d$ guarantees these intervals are taken entirely into one of $U$ or $V$:
In other words,
- $[t_i,t_{i+1}] \subset \sigma^{-1}(U)$ or
- $[t_i,t_{i+1}] \subset \sigma^{-1}(V)$.
Note: We will reuse this fact later.
Start with $[0,t_1]$. Since $\sigma(0)=1\in U$, we have $\sigma[0,t_1] \subset U$. Meanwhile $\pi\bigg|_{[-1/2,1/2]}$ is a homeomorphism to $U$. Let $f$ be the inverse:
We lift $\sigma$ by defining: $$\tilde{\sigma}\bigg|_{[0,t_1]}=f\sigma \bigg|_{[0,t_1]}.$$ It clearly satisfies $\pi\tilde{\sigma}=\sigma$ on $[0,t_1]$.
We continue with induction on $i$: suppose we constructed $\tilde{\sigma}$ with
- $\tilde{\sigma}$ is defined on $[0,t_i]$;
- $\tilde{\sigma}$ is continuous;
- $\pi\tilde{\sigma}=\sigma$ (lift);
- $\tilde{\sigma}$ is the only path with these properties.
Step of induction: let's extend $\tilde{\sigma}$.
- Case 1: $\sigma(t_i)\in U$, then we use $f=\pi^{-1}\bigg|_{(n-1/2,n+1/2)}$;
- Case 2: $\sigma(t_i)\in V$, then we use $f=\pi^{-1}\bigg|_{(n,n+1)}$.
Either way, it's a homeomorphism. Then define: $$\tilde{\sigma}=f\sigma.$$ Verify the four properties for this function (Exercise). $\blacksquare$
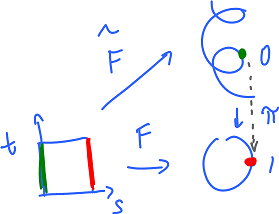
Homotopy-Lifting Lemma. Suppose $F:[0,1]\times[0,1]\to {\bf S}^1$ is a relative homotopy, $F(1,t)=1$. Then there is a unique map $\tilde{F}[0,1]\times[0,1]\to {\bf R}$ (lift) which satisfies: $$\pi\tilde{F}=F,$$ and $F(0,t)=0,t\in T$.
Proof. Similar to the previous:
based on the Lebesgue Lemma, for the square. $\blacksquare$
We use this lemma to show that the homomorphism $\phi$ is one-to-one. It's equivalent to showing that its kernel is $0$.
Suppose $\gamma$ is a path from $0$ to $n$ in ${\bf R}$, then $\pi\gamma$ is homotopic, via $F$, to a constant path: $$\pi\gamma \sim ^F 1.$$ Then we say that it is null-homotopic. By the lemma, we lift $F$ to $\tilde{F}:[0,1]\times [0,1] \to {\bf R}$ with
- $\pi\tilde{F}=F$, and
- $\tilde{F}(0,t)=0$ for $t \in [0,1]$.
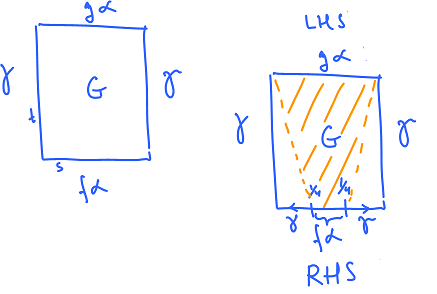
Define $P$ as the subset of the square $[0,1]\times [0,1]$ consisting of its left, right, and bottom edges:
Now, observe that $P$ is connected. Therefore $\tilde{F}(P)$ is connected too $\tilde{F}$ is continuous. But, since $\tilde{F}$'s on $P$ values are integers, $\tilde{F}(P)$ is a point. By property (2), then, $\tilde{F}(P)=0$. And by uniqueness of lifts, the rest of values of $\tilde{F}$ is $0$!
The proof is finished: $$\pi_1({\bf S}^1)={\bf Z}.$$
For a similar analysis in dimension $n$, see homotopy groups. The fundamental group is the first homotopy group, which is why the notation $\pi _1$ is used.
Based maps generate homomorphism of the fundamental groups:
- if $f:X \to Y$ is a map,
- then $f_*:\pi_1(X) \to \pi_1(Y)$ is a homomorphism defined by
$$f_*<\alpha \cdot \beta> =f_*<\alpha> \cdot f_*<\beta>.$$
Compare to homology in dimension 1.
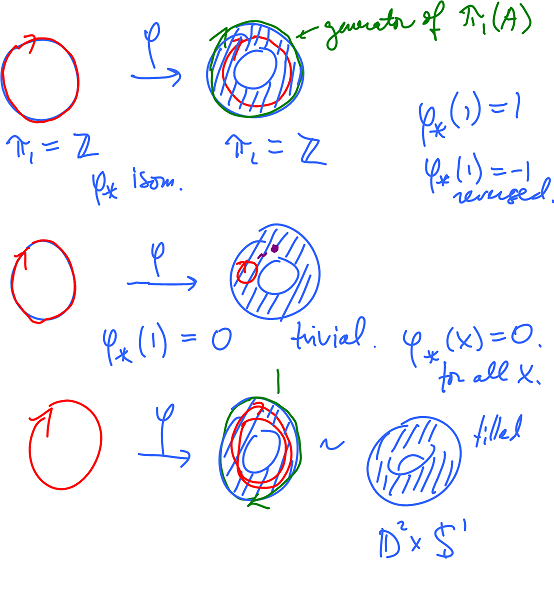
The following are examples of maps from the circle to annulus and what they generate of the fundamental groups:
This leads to the concept of the degree of a map.
Theorem. Suppose $X,Y$ are path-connected. Then $$\pi_1(X\times Y)\cong \pi_1(X)\times \pi_1(Y).$$
Proof. Suppose the base points are $a\in X,b\in Y$. Then select the base point $(a,b)\in X\times Y$. The proof is based on the use of the homomorphisms $p_{X*},p_{Y*}$ generated on the fundamental groups of these spaces by the projections $p_{X},p_{Y}$:
we build a homomorphism $$\phi:\pi_1(X\times Y)\to\pi_1(X)\times \pi_1(Y)$$ defined simply as $$\phi(u)=(p_{X*}(u),p_{Y*}).$$
It is onto. Suppose $\alpha:[0,1]\to X\times Y$ is a path, then so are $\alpha_X=p_X\alpha :[0,1]\to X$ and $\alpha_Y=p_Y\alpha :[0,1]\to Y$. Then $<\alpha>=\phi (<\alpha_X>,<\alpha_Y>)$.
It is one-to-one. Exercise. $\blacksquare$
What if they aren't based?
The basepoints in the same path-component of the space will give isomorphic groups.
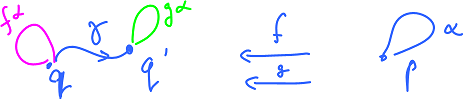
Theorem. Suppose $X$ is path-connected and $p,q \in X$. Then $$\pi _1(X,p) \cong \pi _1(X,q)$$ via the isomorphism: $$P_{\alpha}(<\gamma >)=<\alpha\cdot\gamma\cdot\alpha ^{-1}>,$$ where $\alpha$ is a path connecting $p$ to $q$.
Exercise. Provide the details of the proof.
In particular, this means that the fundamental group of a (non-empty) path-connected space is well-defined, up to isomorphism, without the need to specify a basepoint.
Examples.
- $\pi _1({\bf R}^n)\cong 0$, where ${\bf R}^n$ is the euclidean space.
- $\pi _1({\bf S}^1)\cong\bf{Z}$, where ${\bf S}^1$ is the circle.
- $\pi _1({\bf S}^n)\cong 0$, where ${\bf S}^n$ is the $n$-sphere, $n>1$.
- $\pi _1({\bf T})\cong \bf{Z}\oplus\bf{Z}$, where ${\bf T}$ is the torus.
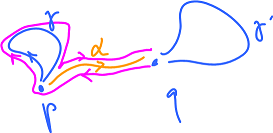
Theorem. Suppose we are given two homotopic maps $$f\sim g:X \to Y.$$ Then $$g_*=P_{\gamma}f_*,$$ where
- $f_*:\pi_1(X,p)\to \pi_1(Y,q),q=f(p)$,
- $g_*:\pi_1(X,p)\to \pi_1(Y,q'),q'=g(p)$.
Proof. Consider:
In the left-hand side of $g_*=P_{\gamma}f_*$ we have
- $g_*(<\alpha>)=<g\alpha>$,
and in the right0hadn side:
- $P_{\gamma}f_*(<\alpha>)=<\gamma^{-1}\cdot (f\alpha)\cdot\gamma >$.
Why are they equal?
All we need to who is that $$g\alpha\sim \gamma^{-1}\cdot (f\alpha)\cdot\gamma.$$ Suppose $F$ is the homotopy between $f$ and $g$. Then let $G(s,t)=F(\alpha(s),t)$. The picture demonstrates that this is the necessary homotopy:
Provide the details (Exercise.). $\blacksquare$