This site is being phased out.
Cell maps
Contents
The definition
Here, we revisit the following issue:
A narrower version of this question is:
Below, we will see how the theory of simplicial maps and their homology is extended to general cell complexes.
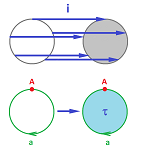
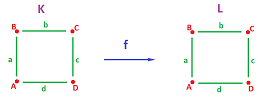
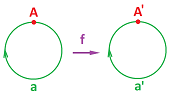
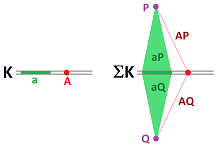
Example (inclusion). As a quick example, consider the inclusion $f$ of the circle into the disk as its boundary:
Here we have: $$f: K = {\bf S}^1 \to L = {\bf B}^2 .$$ After representing the spaces as cell complexes, we examine to what cell in $L$ each cell in $K$ is taken by $f$:
- $f(A) = A,$
- $f(a) = a.$
Further, we compute the chain maps $$f_{i}: C_i(K) \to C_i(L),\ i=0,1,$$ as linear operators by defining them on the generators of these vector spaces:
- $f_0(A) = A,$
- $f_1(a) = a.$
Finally, we compute the homology maps as quotients of these linear operators. These maps reveal what $f$ does to each homology class. Since the $0$-homology groups of $K$ and $L$ are generated by the same cell $A$, this should be an isomorphism: $$[f_0]:H_0(K) = < A > \to H_0(L) = < A >.$$ We also have: $$[f_1]:H_1(K) = < a > \to H_1(L) = 0;$$ therefore, this operator is $0$.
$\square$
The outline of the homology theory we've learned so far is this. The homology is constructed as follows:
Now, if we add maps to this, the procedure is:
We would like to map cell complexes to each other in a manner that lends itself to homological analysis outlined above.
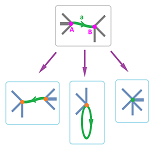
We take the lead from simplicial maps. Under a simplicial map $f$, every $n$-cell $s$ is either
- cloned, $f(s) \approx s$, or
- collapsed, $f(s)$ is an $k$-cell with $k < n$:
The result is used as a template to define cell maps. The difference is that, first, if $f(s)$ is attached to itself along its boundary but $s$ isn't, cloning doesn't produce a homeomorphism -- unless it is seen as limited to the interior $\dot{s}$ of $s$. The construction is illustrated for dimension $1$ below:
The illustration of this construction for dimension $2$ also shows that, different from the simplicial case, a collapsed cell may be stretched over several lower dimensional cells:
Definition. Given two cell complexes $K$ and $L$, a continuous map $$f: |K| \to |L|$$ of their realizations is called a cell map (or cellular map) if for every $k$-cell $s$ in $K$ either
- 1. $f(s)$ is a $k$-cell in $L$ and $f(\dot{s})\approx \dot{s}$ under $f$; or
- 2. $f(s) \subset L^{(k-1)}$, where $L^{(k-1)}$ is the $(k-1)$-skeleton of $L$.
Exercise. List all possible ways complex $K=\{A,a,\alpha\}$ can be mapped to another cell complex.
Exercise. Represent the rotations of a circle through $\pi, \pi /2, \pi/3, \pi/4$ as cell maps.
Example. This projection of a triangle on a line segment is not a cell map:
$\square$
Exercise. Choose a different cell complex to represent $Y$ above in such a way that the projection is then a cell map. How about the rotation of a circle through $\sqrt{2}\pi$?
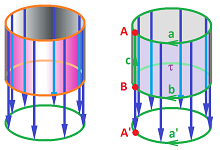
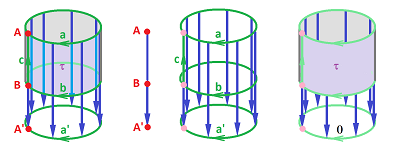
Example (projection). Let's consider the projection of the cylinder on the circle:
We have:
- $f(A) = f(B) = A'$, cloned;
- $f(a) = f(b) = a'$, cloned;
- $f(c) = A'$, collapsed;
- $f(\tau) = a'$, collapsed.
$\square$
Note: the continuity requirement in the definition is crucial. Otherwise, one could, for example, cut the torus into a cylinder, twist it, and then glue it into the Klein bottle while preserving all cells intact.
Examples of cubical maps
The next step after defining a cell map is to construct a function that records what happens to the cells.
Let's consider maps of the “cubical circle” to itself $$f: X = {\bf S}^1 \to Y = {\bf S}^1 .$$ We represent $X$ and $Y$ as two identical cubical complexes $K$ and $L$ and then find an appropriate representation $g:K\to L$ for each $f$ in terms of their cells. More precisely, we are after $$g=f_{\Delta}:C(K)\to C(L).$$
We will try to find several possible functions $g$ under the following condition:
The condition corresponds to the clone/collapse condition for a cell map $f$.
We make up a few examples.
Example (identity). $$\begin{array}{lllllll} g(A) = A, &g(B) = B, &g(C) = C, &g(D) = D, \\ g(a) = a, &g(b) = b, &g(c) = c, &g(d) = d. \end{array}$$
Example (constant). $$\begin{array}{lllllll} g(A) = A, &g(B) = A, &g(C) = A, &g(D) = A, \\ g(a) = 0, &g(b) = 0, &g(c) = 0, &g(d) = 0. \end{array}$$ All $1$-cells collapse. Unlike $f(x)=y,\ \forall x$, there are only $4$ of such maps for these cubical complexes. $\square$
Example (flip). $$\begin{array}{lllllll} g(A) = D, &g(B) = C, &g(C) = B, &g(D) = A, \\ g(a) = c, &g(b) = b, &g(c) = a, &g(d) = d. \end{array}$$ This is a vertical flip; there are also the horizontal and diagonal flips, a total of $4$. Only these four axes allow condition (A) to be satisfied. $\square$
Example (rotation). $$\begin{array}{lllll} g(A) = ?, &g(B) = ?, &g(C) = ?, &g(D) = ?, \\ g(a) = ?, &g(b) = ?, &g(c) = ?, &g(d) = ?. \end{array}$$ $\square$
Exercise. Complete the example.
Next, let's try these values for our vertices: $$g(A) = A, \ g(B) = C,\ ...$$ This is trouble. Even though we can find a cell for $g(a)$, it can't be $AC$ because it's not in $L$. Therefore, $g(a)$ won't be aligned with its end-points. As a result, $g$ breaks apart. To prevent this from happening, we need to require that the end-points of the image in $L$ of any edge in $K$ are the images of the end-points of the edge.
To ensure the cells of all dimensions remain attached after $g$ is applied, we require:
Algebraically, we arrive to the familiar algebraic continuity condition: $$\partial g = g \partial.$$
Exercise. Verify this condition for the examples above.
Observe now that $g$ is defined on complex $K$ but its values aren't technically all in $L$. There are also $0$s. They aren't cells, but rather chains. Recall that, even though $g$ is defined on cells of $K$ only, it can be extended to all chains, by linearity: $$g(A + B) = g(A) + g(B), ...$$
Thus, condition (A) simply means that $g$ maps $k$-chains to $k$-chains. More precisely, $g$ is a collection of functions (a chain map): $$g_k : C_k(K) \to C_k(L),\ k = 0, 1, 2, ....$$ For brevity we use the following notation: $$g : C(K) \to C(L).$$
Example (projection). $$\begin{array}{llllll} g(A) = A, &g(B) = A, &g(C) = D, &g(D) = A, \\ g(a) = 0, &g(b) = d, &g(c) = 0, &g(d) = d. \end{array}$$ Let's verify condition (B): $$\begin{array}{lllllll} \partial g(A) = \partial 0 = 0, \\ g \partial (A) = g(0) = 0. \end{array}$$ Same for the rest of $0$-cells. $$\begin{array}{llllllll} \partial g(a) = \partial (0) = 0,\\ g \partial (a) = g(A + B) = g(A) + g(B) = A + A = 0. \end{array}$$ Same for $c$. $$\begin{array}{lllllll} \partial g(b) = \partial (d) = A + D, \\ g \partial (b) = g(B + C) = g(B) + g(C) = A + D. \end{array}$$ Same for $d$.
$\square$
Exercise. Try the “diagonal fold”: $A$ goes to $C$, while $C, B$ and $D$ stay.
In each of these examples, an idea of a map $f$ of the circle/square was present first, then $f$ was realized as a chain map $g$.
Notation. The chain map of $f$ us denoted by $$g = f_{\Delta} : C(K) \to C(L).$$
Let's make sure that this idea makes sense by reversing this construction. This time, we suppose instead that we already have a chain map $$g : C(K) \to C(L),$$ what is a possible “realization” of $g$: $$f=|g| : |K| \to |L|?$$ The idea is simple: if we know where each vertex goes under $f$, we can construct the rest of $f$ using linearity, i.e., interpolation.
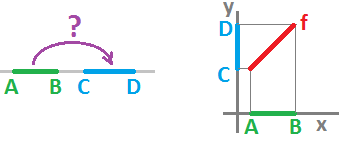
Example (interpolation). A simple example first. Suppose $$K = \{A, B, a :\ \partial a = B-A \},\ L = \{C, D, b:\ \partial b = D-C \}$$ are two complexes representing the closed intervals. Define a chain map: $$g(A) = C,\ g(B) = D,\ g(a) = b.$$
If the first two identities is all we know, we can still build a continuous function $f : |K| \to |L|$ such that $f_{\Delta} = g$. The third identity will be taken care of because of condition (B).
If we include $|K|$ and $|L|$ as subsets of the $x$-axis and the $y$-axis respectively, the solution becomes obvious: $$f(x) := C + \frac{D-C}{B-A} \cdot (x-A).$$ This approach allows us to give a single formula for realizations of all chain operators: $$f(x) := g(A) + \frac{g(B)-g(A)}{B-A} \cdot (x-A).$$ For example, suppose we have a constant map: $$g(A) = C,\ g(B) = C,\ g(a) = 0.$$ Then $$f(x) = C + \frac{C-C}{B-A} \cdot (x-A) = C.$$
$\square$
Of course, this repeats exactly the construction of the geometric realization of a simplicial map. There is no difference as long as we stay within dimension $1$, as in all the examples above. For dimensions above $1$, we can think by analogy.
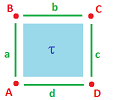
Let's consider a chain map $g$ of the complex $K$ representing the solid square.
Knowing the values of $g$ on the $0$-cells of $K$ gives us the values of $f=|g|$ at those points. How do we extend it to the rest of $|K|$?
An arbitrary point $u$ in $|K|$ is represented as a convex combination of $A, B, C, D$: $$u = sA + tB + pC + qD, \text{ with } s + t + p + q = 1.$$ Then we define $f(u)$ to be $$f(u) := sf(A) + tf(B) + pf(C) + qf(D).$$ Thus, $f(u)$ is a convex combination of $f(A), f(B), f(C), f(D)$. But all of these are vertices of $|L|$, so $f(u) \in |L|$.
Example (projection). Let's consider the projection: $$\begin{array}{llllll} g(A) = A, &g(B) = A, &g(C) = D, &g(D) = A, \\ g(a) = 0, &g(b) = d, &g(c) = 0, &g(d) = d. \\ g(\tau) = 0. \end{array}$$ Then $$\begin{array}{lllllllllll} f(u) &= sf(A) + tf(B) + pf(C) + qf(D) \\ &= sA + tA + pD + qD \\ &= (s+t)A + (p+q)D. \end{array}$$ Since $(s+t) + (p+q) = 1$, we conclude that $f(u)$ belongs to the interval $AD$.
$\square$
Exercise. Is this map well-defined? Hint: the construction for simplicial maps is based on barycentric coordinates.
Modules
Before we proceed to build the homology theory of maps, we review the setup of arbitrary ring of coefficients $R$.
Recall that
- with $R={\bf Z}$, the chain groups and the homology are abelian groups, and
- with $R={\bf R}$ (or other fields), the chain groups and the homology are vector spaces,
- with an arbitrary $R$, the chain groups and the homology are modules.
Informally,
The following definitions and results can be found in standard literature such as Algebra by Hungerford (chapter IV).
Definition. Given a commutative ring $R$ with the multiplicative identity $1_R$, a (commutative) $R$-module $M$ consists of an abelian group $(M, +)$ and a scalar product operation $R \times M \to M$ such that for all $r,s \in R$ and $x, y \in M$, we have:
- $r(x+y) = rx + ry$,
- $(r+s)x = rx + sx$,
- $(rs)x = r(sx)$,
- $1_Rx = x$.
The scalar multiplication can be written on the left or right.
If $R$ is a field, an $R$-module is a vector space.
The rest of the definitions are virtually identical to the ones for vector spaces.
A subgroup $N$ of $M$ is a submodule if it is closed under scalar multiplication: for any $n \in N$ and any $r\in R$, we have $rn \in N$.
A group homomorphism $f: M \to N$ is a (module) homomorphism (or a linear operator) if it preserves the scalar multiplication: for any $m,n \in M$ and any $r, s \in R$, we have $f(rm + sn) = rf(m) + sf(n)$.
A bijective module homomorphism is an (module) isomorphism, and the two modules are called isomorphic.
Exercise. Prove that this is a category.
The kernel of a module homomorphism $f : M \to N$ is the submodule of $M$ consisting of all elements that are taken to zero by $f$. The isomorphism theorems of group theory are still valid.
A module $M$ is called finitely generated if there exist finitely many elements $v_1,v_2,...,v_n \in M$ such that every element of $M$ is a linear combination of these elements (with coefficients in $R$).
A module $M$ is called free if it has a basis. This condition is equivalent to this: $M$ is isomorphic to a direct sum of copies of the ring $R$. Every submodule $L$ of such a module is a summand: $$M=L\oplus N,$$ for some other submodule $N$.
Of course, ${\bf Z}^n$ is free and finitely generated. It is our primary interest as it has appeared as chain groups. It behaves very similarly to ${\bf R}^n$ and the main differences lie in these two areas.
First, the quotients may have torsion, such as in ${\bf Z}/ 2{\bf Z} \cong {\bf Z}_2$. We have seen this happen in our computations of the homology groups.
Second, some operators invertible over ${\bf R}$ may be singular over ${\bf Z}$. For example, $f(x)=2x$.
We will refer to finitely generated free modules as simply modules.
The topological step
The topological setup above is now translated into algebra. From a cell map, we construct maps on the chain groups of the two cell complexes.
Definition. Given a cell map $f: |K| \to |L|$, the $k$th chain map generated by map $f$, $$f_k: C_k(K) \to C_k(L),$$ is defined on the generators as follows. For each $k$-cell $s$ in $K$,
- 1. if $s$ is cloned by $f$, define $f_k(s) := \pm f(s)$, with the sign determined by the orientation of the cell $f(s)$ in $L$ induced by $f$;
- 2. if $s$ is collapsed by $f$, define $f_k(s) := 0$.
Also, $$f_{\Delta} = \{f_i:i=0,1,... \}:C(K)\to C(L)$$ is the (total) chain map generated by $f$.
In the definition's left-hand sides, we have the values of $s$ under $f_k$, while in the right hand sides, we have the images of $s$ under $f$.
Note: The notion of orientation was fully developed for both simplicial and cubical complexes. For the general case of cell complexes, we just point out that for dimensions $0$ and $1$ the notion applies without change, while in dimension $2$ the orientation of a cell is simply the direction of a trip around its boundary. Also, we can avoid dealing with the issue of orientation by resigning, with a certain penalty, to the algebra over $R={\bf Z}_2$.
Example (projection). Let consider the projection of the cylinder on the circle again:
From the images of the cells under $f$ listed above, we conclude:
- $f_0(A) = f_0(B) = A';$
- $f_1(a) = f_1(b) = a';\ f_1(c) = 0;$
- $f_2(\tau) = 0.$
Now we need to compute the operators:
- $f_0:\ C_0(K) = < A, B > \to C_0(L) = < A' >;$
- $f_1:\ C_1(K) = < a, b, c >\to C_1(L) = < a' >;$
- $f_2:\ C_2(K) = < \tau > \to C_2(L) = 0.$
From the values of the operators on the basis elements, we conclude:
- $f_0 = [1, 1];$
- $f_1 = [1, 1, 0];$
- $f_2 = 0.$
$\square$
Recall also that a chain map as a combination of maps between chain complexes, in addition, has to take boundary to boundary, or, more precisely, has to commute with the boundary operator.
Theorem. If $f$ is a cell map, then $f_{\Delta}$ is a chain map: $$\partial_kf_k = f_{k-1}\partial_k,\ \forall k.$$
Proof. Done for simplicial maps. $\blacksquare$
Example. To continue the above example, the diagram has to commute: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{c|cccccccccccccc} & 0 & \ra{\partial_3} & C_2 & \ra{\partial_2} & C_1 & \ra{\partial_1} & C_0 & \ra{\partial_0} &0 \\ \hline C(K): & 0 & \ra{0} & {\bf R} & \ra{\partial_2} & {\bf R}^3 & \ra{\partial_1} & {\bf R}^2 & \ra{0} &0 \\ f_{\Delta}: & \ \da{0} & & \ \da{f_2} & & \ \da{f_1} & & \ \da{f_0} & & \ \da{0}\\ C(L): & 0 & \ra{0} & 0 & \ra{\partial_2} & {\bf R} & \ra{\partial_1} & {\bf R} & \ra{0} &0 \\ \end{array} $$
Let's verify that the identity is satisfied in each square above. First we list the boundary operators for the two chain complexes: $$\begin{array}{llllllllll} \partial^K_2(\tau)=a-b, &\partial^K_1(a)=\partial^K_1(b)=0, \partial^K_1(c)=A-B, &\partial^K_0(A)=\partial^K_0(B)=0;\\ \partial^L_2=0, &\partial^L_1(a')=0, &\partial^L_0(A')=0. \end{array}$$ Now we go through the diagram from left to right. $$\begin{array}{l|l|l|l} \partial_2f_2(\tau) = f_1\partial_2(\tau)&{\partial}_1f_1(a) = f_0{\partial}_1(a)&\partial_1f_1(b) = f_0\partial_1(b)&{\partial}_1f_1(c) = f_0{\partial}_1(c)\\ \partial_2(0) = f_1(a - b) &{\partial}_1(a') = f_0(0)&\partial_1(a') = f_0(0)&{\partial}_1(0) = f_0(B - A) = A' - A'\\ 0 = a' - a' = 0, {\rm \hspace{3pt} OK}&0 = 0, {\rm \hspace{3pt} OK}&0 = 0, {\rm \hspace{3pt} OK}&0 = 0, {\rm \hspace{3pt} OK} \end{array}$$
So, $f_{\Delta}$ is indeed a chain map.
$\square$
Exercise. Represent the cylinder as a complex with two $2$-cells, find an appropriate cell complex for the circle and an appropriate cell map for the projection, compute the chain map, and confirm that the diagram commutes.
Note: a broader definition of cell map is used as well: $f(K^n)\subset L^n$. It can be proven that the two definitions are equivalent, up to homotopy.
The algebraic step
For a cell map, we have defined -- by topological means -- its chain maps as the homomorphisms between the chain groups of the complexes. At this point, we can ignore the origin of these new maps and proceed to homology in a purely algebraic manner. Fortunately, this part was fully developed for simplicial complexes and maps and, being algebraic, the development is identical for cell complexes. A quick review follows.
First, we suppose that we have two chain complexes, i.e., combinations of modules and homomorphisms between these modules, called the boundary operators: $$M=\{M_i,\partial^M_i:\ M_i\to M_{i-1}:\ i=0,1,...\},$$ $$N=\{N_i,\partial^N_i:\ N_i\to N_{i-1}:\ i=0,1,...\},$$ with $$M_{-1}=N_{-1}=0.$$ As chain complexes, they are to satisfy the “double boundary condition”: $$\partial^M_i \partial^M_{i+1} =0,\ i=0,1,2,...;$$ $$\partial^N_i \partial^N_{i+1} =0,\ i=0,1,2,....$$ The compact form of this condition is: $$\partial\partial =0.$$
Second, we suppose that we have a chain map as a combination of homomorphisms between the corresponding items of the two chain complexes: $$f_{\Delta}=\{f_i:\ M_i\to N_i:\ i=0,1,...\}:M\to N.$$ As a chain map, it is to satisfy the “algebraic continuity condition”: $$\partial^M_i f_i = f_{i-1} \partial^N_i,\ i=0,1,....$$ The compact form of this condition is: $$f\partial =\partial f.$$ Moreover, the diagram commutes: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccccccccccc} M_{i+1}& \ra{\partial^M_{i+1}} & M_{i}\\ \da{f_{i+1}}& \searrow & \da{f_{i}}\\ N_{i+1}& \ra{\partial^N_{i+1}} & N_{i}. \end{array} $$
This combination of modules and homomorphisms forms a diagram with the two chain complexes occupying the two rows and the chain map connecting them by the vertical arrows, item by item: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccccccccccccccc} ...& \to & M_{k+1}& \ra{\partial^M_{k+1}} & M_{k}& \ra{\partial^M_{k}} & M_{k-1}& \to &...& \to & 0\\ ...& & \da{f_{k+1}}& & \da{f_{k}}& & \da{f_{k-1}}& &...& & \\ ...& \to & N_{k+1}& \ra{\partial^N_{k+1}} & N_{k}& \ra{\partial^N_{k}} & N_{k-1}& \to &...& \to & 0. \end{array} $$ Each square commutes.
Next, we define the homology groups of the chain complex for either of them, as these quotient modules: $$H_i(M)=\frac{\ker \partial^M_i }{\operatorname{Im} \partial^M_{i+1}},i=0,1,...;$$ $$H_i(N)=\frac{\ker \partial^N_i }{\operatorname{Im} \partial^N_{i+1}},i=0,1,....$$ And we use the following compact notation: $$H(M)=\{H_i(M):\ i=0,1,...\},$$ $$H(N)=\{H_i(N):i\ =0,1,...\}.$$
Finally, the homology map induced by the chain map $$f_{\Delta}=\{f_0,f_1,...\}:M\to N,$$ is defined as the combination: $$f_*=\{[f_0],[f_1],...\}:H(M)\to H(N),$$ of the quotient maps of $f_i$: $$[f_i]: H_i(M) \to H_i(N),\ i=0,1,....$$ In other words, each one is a homomorphism defined by $$[f_i]([x]) := [f_i(x)].$$ The homology map is well-defined as guaranteed by the two properties above.
Meanwhile, under this equivalence relation the quotients of the boundary operators are trivial: $$[\partial^M_i]=0,\ [\partial^N_i]=0,\ i=0,1,....$$
Exercise. Prove these identities.
Then, under the quotients, the above diagram of chain complexes is distilled into this: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccccccccccccc} ...& \to & H_{k+1}(M)& \ra{0} & H_{k}(M)& \ra{0} & H_{k-1}(M)& \to &...& \to & 0\\ ...& & \da{[f_{k+1}]}& & \da{[f_{k}]}& & \da{[f_{k-1}]}& &...& & \\ ...& \to & H_{k+1}(N)& \ra{0} & H_{k}(N)& \ra{0} & H_{k-1}(N)& \to &...& \to & 0. \end{array} $$ Even though still technically commutative, the diagram is essentially just a collection of columns. They are combined into our very compact notation: $$f_*:H(M)\to H(N).$$
Example. From the last subsection, we have the following chain maps: $$\begin{array}{lllllllllll} f_0: & M_0 = < A, B > & \to & N_0 = < A' >, & f_0(A) = f_0(B) = A';\\ f_1: & M_1 = < a, b, c > & \to & N_1 = < a' >, & f_1(a) = f_1(b) = a', f_1(c) = 0;\\ f_2: & M_2 = < \tau > & \to & N_2 = 0, & f_2(\tau) = 0.\ \end{array}$$ From the algebraic point of view, the nature of these generators is irrelevant. Now, the diagram is: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{c|cccccccccc} & 0 & \ra{\partial_3} & C_2 & \ra{\partial_2} & C_1 & \ra{\partial_1} & C_0 & \ra{\partial_0} &0 \\ \hline M: & 0 & \ra{0} & < \tau > & \ra{[1,-1,0]^T} & < a, b, c > & \ra{\left[\begin{array}{ccc}0&0&-1\\0&0&1\end{array}\right]} & < A,B > & \ra{0} &0 \\ f_{\Delta}: & \da{0} & & \da{0} & & \da{[1,1,0]} & & \da{[1,1]} & & \da{0}\\ N: & 0 & \ra{0} & 0 & \ra{0} & < a' > & \ra{0} & < A' > & \ra{0} & 0 \end{array} $$ Compute the homology: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{c|ccccccccccccc} & H_2 & & H_1 & & H_0 \\ \hline M: & 0 & & < [a]=[b] > & & < [A]=[B] > \\ f_*: & \da{0} & & \da{[1]} & & \da{[1]} \\ N: & 0 & & < [a'] > & & < [A'] > \end{array} $$ $\square$
Exercise. For the chain complexes $M,N$ above, suggest three examples of chain maps $g:N\to N$ and compute their homology maps. Make sure that all of them are different from the homology map above. Hint: make no references to cell maps.
Examples of homology maps
What happens to homology classes under continuous functions?
Let's consider a few examples with some typical maps that exhibit common behavior.
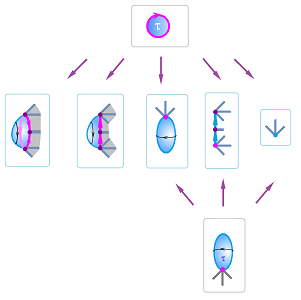
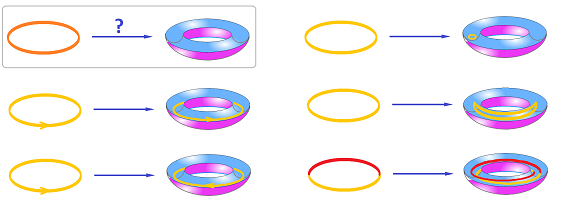
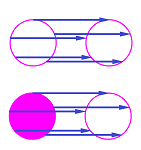
We start with maps of the circle to itself. Such a map can be thought of as a circular rope, $X$, being fitted into a circular groove, $Y$. You can carefully transport the rope to the groove without disturbing its shape to get the identity map, or you can compress it into a tight knot to get the constant map etc.:
To have a cell map representation for these maps, we use the following cell complexes of the circles:
Example (constant). If $f: X \to Y$ is a constant map, all $k$-homology classes of $X$ with $k>0$ collapse or, algebraically speaking, are mapped to $0$ by $f_*$. Meanwhile, all $0$-homology classes of $X$ are mapped to the same $0$-homology class of $Y$. So, it's the identity for any path-connected spaces.
$\square$
Example (identity). If $f$ is the identity map, we have $$\begin{array}{llllll} f_*(A) = A', \\ f_*(a) = a'. \end{array}$$ $\square$
Example (flip). Suppose $f$ is a flip (a reflection about the $y$-axis) of the circle. Then $$f_*(a) = -a'.$$ $\square$
Example (turn). You can also turn (or rotate) the rope before placing it into the groove. The resulting map is very similar to the identity regardless of the degree of the turn. Indeed, then we have: $$f_*(a) = a'.$$ Even though the map is simple and its homology interpretation is clear, this isn't a cell map!
$\square$
Example (wrap). If you wind the rope twice before placing it into the groove, you get: $$f_*(a) = 2a'.$$ Again, this isn't a cell map!
$\square$
Example (inclusion). In the all examples above we have $$f_*(A) = A'.$$ Let's consider an example that illustrates what else can happen to $0$-classes. Consider the inclusion of the two end-points of a segment into the segment. Then $f : X = \{A, B\} \to Y = [A,B]$ is given by $f(A) = A,\ f(B) = B$. Now, even though $A$ and $B$ aren't homologous in $X$, their images under $f$ are, in $Y$. So, $f(A) \sim f(B)$. In other words, $$f_*([A]) = f_*([B]) = [A] = [B].$$ Algebraically, $[A] - [B]$ is mapped to $0$.
$\square$
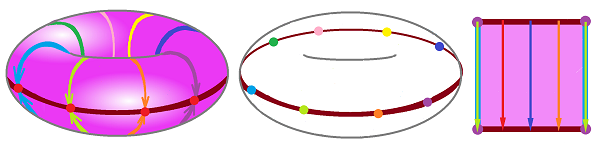
Example (collapse). A more advanced example of collapse is that of the torus to a circle, $f: X = {\bf T}^2 \to Y = {\bf S}^1$.
We choose one longitude $L$ (in red) and then move every point of the torus to its nearest point on $L$.
$\square$
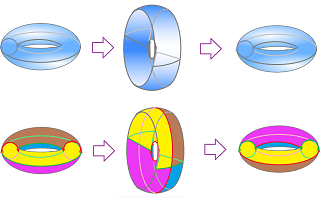
Example (inversion). And here's turning the torus inside out:
$\square$
Exercise. Consider the following self-maps of the torus ${\bf T}^2$:
- (a) collapsing it to a meridian,
- (b) collapsing it to the equator (above),
- (c) collapsing a meridian to a point,
- (d) gluing the outer equator to the inner equator,
- (e) turning it inside out.
For each of those,
- describe the cell structure of the complexes,
- represent the map as a cell map,
- compute the chain maps of this map, and
- compute the homology maps of these chain maps.
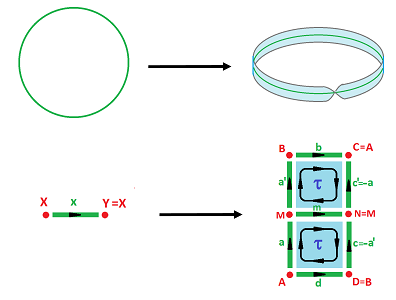
Example (inclusion). We consider maps from the circle to the Mobius band: $$f:{\bf S}^1 \to {\bf M}^2.$$ First, we map the circle to the median circle of the band:
As you can see, we have to subdivide the band's square into two to make this map into a cell map. Then we have: $$f(X)=f(Y)=M;$$ $$f(x)=m.$$ Then, since $f_1(x)=m$, one can see that the $1$st homology map is the identity: $$f_*=\operatorname{Id}:H_1(K)={\bf Z} \to H_1(L)={\bf Z}.$$
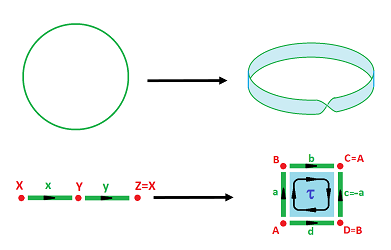
Second, we map the circle to the edge of the band:
As you can see, we have to subdivide the circle's edge into two edges to make this map into a cell map. Then we have: $$f(X)=B,\ f(Y)=A;$$ $$f(x)=b,\ f(y)=d.$$ Then, since $f_1(x+y)=b+d$, one can see that the $1$st homology map is not the identity: $$f_*=2\cdot\operatorname{Id}:H_1(K)={\bf Z} \to H_1(L)={\bf Z}.$$ $\square$
Exercise. Provide details of the homology computations in the last example.
Exercise. Consider a few possible maps for each of these and compute their homology maps:
- inclusions of the circle into the torus;
- self-maps of the figure eight;
- inclusions of the circle to the sphere.
Homology theory
Let's review how the theory is built one more time:
That's the whole theory.
Now, algebraically: $$\begin{array}{cccccccccc} f: &|K| &\to & |L|& \leadsto \\ \\ f_{\Delta}: &C(K) & \to & C(L) & \leadsto\\ \\ f_*: &H(K) &\to &H(L).\\ \end{array}$$
We recognize each of these three settings as categories:
- cell complexes and cell maps,
- chain complexes and chain maps,
- modules and homomorphisms.
Indeed, in each of them, we can always complete this diagram by composition: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccccccc} &X & \ra{f} & Y \\ & & _{gf} \ddots & \da{g} \\ & & & Z \end{array} $$
Let's, again, consider these two steps separately.
First, the topological step. It relies on these familiar theorems.
Theorem. The identity cell map induces the identity chain map: $$\left( \operatorname{Id}_{ |K| } \right) _i= \operatorname{Id}_{ C_i(K) }.$$
Theorem. The chain map of the composition of two cell maps is the composition of their chain maps: $$(gf)_i = g_if_i.$$
Next the algebraic step.
Theorem. The identity chain map induces the identity homology map: $$\left( \operatorname{Id}_{ C(K) } \right)_*= \operatorname{Id}_{ H(K) }.$$
Theorem. The homology map of the composition of two chain maps is the composition of their homology maps: $$(gf)_* = g_*f_*.$$
Now, we combine the two steps omitting the intermediate state. Recall that, when the chain complex $M=C(K)$ comes from a cell complex $K$, we have been replacing the cumbersome $H(C(K))$ with $H(K)$ (as well as $H(C(K,K'))$ with $H(K,K')$).
The following is obvious.
Theorem. The identity cell map induces the identity homology map: $$\left( \operatorname{Id}_{ |K| } \right)_*= \operatorname{Id}_{ H(K) }.$$
Theorem. The homology map of the composition of two cell maps is the composition of their homology maps $$(gf)_* = g_*f_*.$$
The main result is below.
Theorem. Suppose $K$ and $L$ are cell complexes, if a map $$f : |K| \to |L|$$ is a cell map and a homeomorphism, and $$f^{-1} : |L| \to |K|$$ is a cell map too, then the homology map $$f_* : H_k(K) \to H_k(L)$$ is an isomorphism for all $k$.
Proof. From the definition of inverse function, $$ff^{-1} = \operatorname{Id}_{|L|},$$ $$f^{-1}f = \operatorname{Id}_{|K|}.$$ From the above theorems, it follows that $$f_*(f^{-1})_* = \operatorname{Id}_{ H(L) },$$ $$(f^{-1})_* f_* = \operatorname{Id}_{ H(K) }.$$ $\blacksquare$
The theorems prove that the effect of either of these two steps:
- from the category of cell complexes to the category of chain complexes; and then
- from the category of chain complexes to the category of modules, $\\$
is that objects are mapped to objects and morphisms to morphisms -- in such a way that the compositions are preserved. Of course, the combination of these two steps has the same effect.
Functors
The results in the last subsection have a far-reaching generalization.
Definition. A functor ${\mathscr F}$ from category ${\mathscr C}$ to category ${\mathscr D}$ consists of two functions:
- the first associates to each object $X$ in ${\mathscr C}$ an object ${\mathscr F}(X)$ in ${\mathscr D}$,
- the second associates to each morphism $f: X\to Y$ in ${\mathscr C}$ a morphism ${\mathscr F}(f):{\mathscr F}(X) \to {\mathscr F}(Y)$ in ${\mathscr D}$.
In other words, a functor is a combination of these two: $${\mathscr F}:\operatorname {Obj}({\mathscr C}) \to \text{Obj} ({\mathscr D}),$$ and, if ${\mathscr F}(X)=U,\ {\mathscr F}(Y)=V$, we have $${\mathscr F}={\mathscr F}_{X,Y}:\text{Hom}_{\mathscr C}(X,Y) \to \operatorname {Hom}_{\mathscr D}(U,V).$$ We assume that the following two conditions hold:
- (identity) ${\mathscr F}(\operatorname{Id}_{X}) = \operatorname{Id}_{{\mathscr F}(X)}$, for every object $X$ in ${\mathscr C}$;
- (compositions) ${\mathscr F}(g f) = {\mathscr F}(g) {\mathscr F}(f)$, for all morphisms $f:X \to Y$, and $g:Y\to Z$.
The latter condition can be illustrated with a commutative diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccccccccccc} &X & \ra{f} & Y & & {\mathscr F}(X) & \ra{{\mathscr F}(f)} & {\mathscr F}(Y)\\ & & _{gf}\ddots & \ \da{g} & \leadsto & & _{{\mathscr F}(gf)}\ddots & \ \ \da{{\mathscr F}(g)}\\ & & & Z & & & & {\mathscr F}(Z) \end{array} $$
Exercise. Define the trivial functor.
A slightly more complex is a forgetful functor: it is a functor that strips all structure off a given category and leaves us with the category of sets. For example, for groups we have: $${\mathscr F}((G,*))=G.$$
Exercise. Prove that the composition of two functors is a functor.
Back to homology. Above, we proved the following:
Theorem. Homology is a functor from cell complexes and maps to abelian groups and homomorphisms.
Exercise. Explain in what sense a chain complex is a functor.
Exercise. Outline the homology theory for relative cell complexes and cell maps of pairs. Hint: $C(K,K')=C(K) / C(K')$.
This is how purely “functorial” aspects of homology theory are applied.
Example (extension). Suppose we would like to answer the following question:
- Can a soap bubble contract to the ring without tearing?
We recast this question as an example of the Extension Problem:
- Can we extend the map of the circle onto itself to the whole disk?
In other words, is there a continuous $F$ to complete the first diagram below so that it is commutative? Here, we translate our initial topological diagram -- with cell complexes and cell maps -- into algebra -- with groups and homomorphisms: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccccccccccccc} {\bf S}^{n-1} & \hookrightarrow & {\bf B}^{n} && & H_{n-1}({\bf S}^{n-1}) & \to & H_{n-1}({\bf B}^{n}) & & {\bf Z} & \to & 0 \\ & \searrow ^{\operatorname{Id}}& \ \ \da{F=?} && \leadsto & _{} & \searrow ^{\operatorname{Id}} & \ \da{?} & = & & \searrow ^{\operatorname{Id}}& \da{?}\\ & & {\bf S}^{n-1} && & & & H_{n-1}({\bf S}^{n-1}) & & & & {\bf Z} \end{array}$$ The latter is easy to evaluate, which produces the third diagram. This diagram is impossible to complete!
$\square$
Exercise. Provide such analysis for extension of the identity map of the circle to the circle to that of the torus.
Exercise. For each $n\in {\bf Z}$, construct a map from the circle to the Mobius band: $$f:K={\bf S}^1 \to L={\bf M}^2,$$ following the pattern we saw in the last subsection:
and confirm that its $1$st homology map is the multiplication by $n$: $$f_*=n\cdot \operatorname{Id}:H_1(K)={\bf Z} \to H_1(L)={\bf Z}.$$
Exercise. List possible maps for each of these based on the possible homology maps:
- inclusions of the circle into the torus;
- self-maps of the figure eight;
- inclusions of the circle to the sphere.
New maps from old
We have been using tools for building new topological spaces from old. The main ones are the product and the quotient. Both come with a way to construct appropriate new maps. Let's review.
For two spaces $X,Y$, their product is a topological space defined on the product set $X\times Y$ with the product topology. If there are maps $$f:X\to Y, \ f':X'\to Y',$$ the product map $$f\times f':X\times X' \to Y\times Y',$$ of these maps is, of course, $$\left(f\times f'\right)(x,y):=\left(f(x),f(y)\right).$$ It is always well-defined.
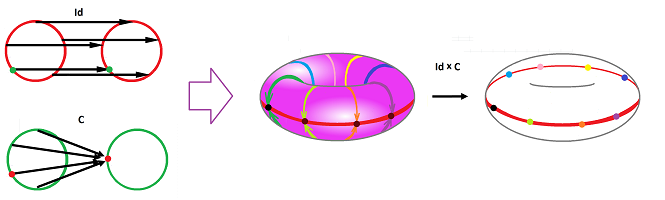
Example. Suppose $X,Y$ both are the circle. Then the product of the identity and a constant map collapses the torus on the equator:
$\square$
Exercise. Represent, when possible, as product maps the following maps of the torus: constant, collapse to a meridian, collapse to the bottom half, collapse to the diagonal, rotation about its axis, reflection about a vertical plane.
Exercise. For any $Q^m$ an $m$-cube, suppose we have an identification map $$f_m:Q^m\to {\bf S}^m, \ f(\partial Q^m)=\{a\},\ a\in {\bf S}^m.$$ Describe $f_m \times f_n$.
It follows that fixing one of the spaces creates a simple functor, such as: $${\mathscr F}(X):={\bf I}\times X, \ {\mathscr F}(f):=\operatorname{Id}\times f. $$
For a space $X$ and an equivalence relation on it, the quotient is a topological space defined on the quotient set $X / _{\sim}$ with the quotient topology. If there is a map $$f:X\to Y,$$ the quotient map $$[f]:X / _{\sim} \to Y/ _{\sim} ,$$ of this map is, of course, $$[f]([x]):=[f(x)].$$ It is well-defined when $x\sim y \Rightarrow f(x) \sim f(y).$
Example (wrap). Suppose $f$ is the “double wrap” of the circle. Then $f\times \operatorname{Id}$ is the “double wrap” of the cylinder.
Suppose the equivalence relation collapses the top and the bottom edges of the cylinder, separately. Then $[f\times \operatorname{Id}]$ is the “double wrap” of the resulting sphere.
$\square$
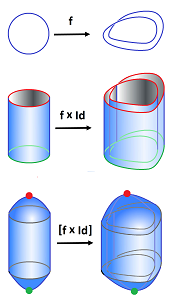
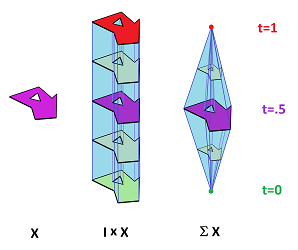
Unless both of the spaces are non-trivial, the product won't create any new topological features; indeed: $${\bf I}\times X \simeq X .$$ The flip side is that we can use products to create new building blocks from old, such as cubes: $${\bf I}\times Q^n = Q^{n+1} .$$ The simplicial analog of this construction is the cone which is simply adding an extra vertex to the simplex: $$\operatorname{C}\sigma^n=\sigma^{n+1} .$$ Both increase the dimension by $1$!
There is also the cone construction for topological spaces. Given a space $X$, first form the product ${\bf I} \times X$, then collapse the top to a point: $$\operatorname{C} X:= \left( {\bf I} \times X \right)/ _{\{1\}\times X} \ .$$ The result is contractible: $$\operatorname{C}X \simeq \{p\} .$$ For example, the cone of the circle is simply the disk.
However, two of such cones glued together will produce the sphere!
This is how. First form the product ${\bf I} \times X.$ Nothing new here. Then create the quotient by collapsing the top to a point and the bottom to a point.
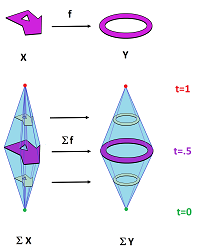
Definition. Given a topological space $X$, define the suspension of $X$ to be $$\Sigma X:= \left( {\bf I} \times X \right)/ _{\sim},$$ where the equivalence relation is given by: $$(0,x)\sim (0,y),\ (1,x)\sim (1,y).$$
Without the second part, this is the cone of $X$.
Exercise. Given a triangulation of $X$, construct a triangulation of $\Sigma X$. Hint: use cones.
The idea is to use suspension to create new spaces with new, higher dimensional, topological features. However, these features don't come from nowhere; compare:
- $\Sigma {\bf S}^1 \approx {\bf S}^{2}$, a non-trivial $2$-class is produced from a non-trivial $1$-class; but
- $\Sigma {\bf B}^1 \approx {\bf B}^2$, trivial $1$-classes don't produce non-trivial $2$-classes.
For the spheres, things are simple:
Proposition. $$\Sigma {\bf S}^n \approx {\bf S}^{n+1},\ n=0,1,2,....$$
Exercise. Prove the proposition.
Let's express the homology of the suspension $\Sigma X$ in terms of the homology of $X$. The proposition implies: $$H_{n+1}(\Sigma {\bf S}^n ) \cong H_n({\bf S}^{n}).$$ The case of $n=0$ is an exception though. Indeed, $${\bf S}^0=\{p,q\}\Rightarrow H_0({\bf S}^0)={\bf Z}\oplus {\bf Z}.$$ A convenient way of treating this exception is given by the reduced homology.
Theorem. For a cell complex $K$, we have $$\tilde{H}_{n+1}(\Sigma K) \cong \tilde{H}_n(K),\ n=0,1,2,....$$
Exercise. Prove the theorem for simplicial complexes. Hint: Write the two chain complexes and suggest a kind of chain map between them that raises the dimension.
Definition. Given a map $f:X\to Y$, there is a map between the suspensions, $$\Sigma f:\Sigma X\to \Sigma Y,$$ called the suspension map of $f$, defined by $$(\Sigma f)([t,x]):=[t,f(x)].$$
Then, for a map $f$ of the circles, its suspension is built by repeating $f$ on the equator and all other longitudes. In particular, the “double wrap” of the sphere is the suspension of the “double wrap” of the circle, as shown above.
Exercise. Prove that the suspension map is well-defined.
Exercise. Prove that $\Sigma$ is a functor from the category of topological spaces into itself.
Let's express the homology map of the suspension map $\Sigma f$ in terms of the homology map of $f$.
Theorem. Given a cell map $f:K\to L$, the following diagram is commutative for every $n=0,1,...$: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{cccccccccc} \tilde{H}_n(K) & \ra{f_*} & \tilde{H}_n(L) \\ \da{\cong} & & \da{\cong} \\ \tilde{H}_{n+1}(\Sigma K) & \ra{(\Sigma f)_*} & \tilde{H}_{n+1}(\Sigma L). \\ \end{array}$$
Exercise. Prove the theorem for simplicial maps.