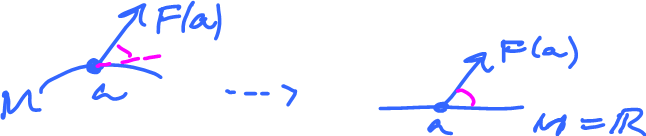Tangent bundles and differential forms

$1$-forms as maps on the tangent bundle

Recall, a continuous $1$-form in ${\bf R}^3$ is a function $$\varphi \colon {\bf R}^3 \times {\bf R}^3 \rightarrow {\bf R}.$$ The first ${\bf R}^3$ is $(x,y,z)$ and the second one is $(dx,dy,dz)$. The function is linear on $dx,dy,dz$, differentiable on $x,y,z$.

Now, suppose we have a $3$-manifold $M^3$. Then we commonly refer to functions defined on it maps.

Definition: A continuous differential form of degree $1$ is a map $$\varphi \colon TM \rightarrow {\bf R},$$ linear on the tangent vectors in $T_aM$ for each $a \in M$.

To ensure that for each $a \in M$, there is a tangent space, we assume that $M$ is smooth.

In the Cartesian case,

• $M={\bf R}^3$,
• $T_aM = {\bf R}^3$,
• $TM={\bf R}^3 \times {\bf R}^3$.

For the general, manifold, case we assume that $$M \subset {\bf R}^N.$$ And the latter has differential forms already!

Again: $$\varphi \colon TM = \displaystyle\bigsqcup_{a \in M} T_aM \rightarrow {\bf R}$$ require $\varphi$ is linear on each $T_aM, a \in M$.

What is a vector field on a manifold?

In ${\bf R}^n$, vector field is $$F \colon {\bf R}^n \rightarrow {\bf R}^n$$ or $$F \colon {\rm point \hspace{3pt}} a \mapsto {\rm vector \hspace{3pt}} F(a).$$

In $M$, is it the same? $$F \colon {\rm point \hspace{3pt}} a \mapsto {\rm vector \hspace{3pt}} F(a)?$$ But where would $F(a)$ live?

Problem: $F(a) \not\in M$!

Instead we do the following.

Definition: Suppose $F \colon M \rightarrow TM$ is a function such that $F \colon {\rm point \hspace{3pt}} a \mapsto {\rm vector \hspace{3pt}}$ in $T_aM$, then we call $F$ a vector field on $M$.

This makes sense if you consider motion: a car on the road, a roller-coaster ride, and parametric curves in general.

We can compose vector fields and $1$-forms now, as functions:

.

Given $F \colon M \rightarrow TM$ and $\varphi \colon TM \rightarrow {\bf R}$, then $\varphi F \colon M \rightarrow {\bf R}$ makes sense.

This allows us to define differentiability of forms on manifolds.

Definition: A $1$-form $\varphi$ is called $C^k$, if for every $C^k$ vector field $F$, $\varphi F$ is $C^k$ too.

recall, a differentiable, specifically, $C^k$, form $\varphi \colon {\bf R}^3 \times {\bf R}^3 \rightarrow {\bf R}$ is differentiable, $C^k$, with respect to $x,y,z$. It's continuous for $k=0$.

The vector space of forms on a manifold

Let's connect these forms with the familiar ones: $dx,dy,dz$.

Recall that we have seen them in ${\bf R}^3$ as $1$-forms: $$dx \colon {\bf R}^3 \times {\bf R}^3 \rightarrow {\bf R}.$$ Here the first component is "smooth" and the second component is "linear".

Select a point $a \in {\bf R}^3$ (fixed!). Then we need to understand $$(dx)(a,v),$$ where vector $v \in {\bf R}^3$. Read this as a function, $dx$, evaluated at a point, $(a,v)$.

What is this equal to, for a given $v$?

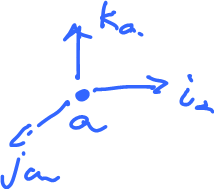
Let $i,j,k$ be the standard basis of ${\bf R}^3$. We'll use the same letters for the bases of $T_aM$, even though technically these are different for each point, like this: $i_a$ is attached to $a$, $i_b$ is attached to $b$, etc.

Since $dx$ is linear, we only need to define it on the basis vectors: $$\begin{align*} (dx)(a,i)&=1, \\ (dx)(a,j)&=0, \\ (dx)(a,k)&=0. \end{align*}$$

Then for $a=(a_1,a_2,a_3)$ and $v=(v_1,v_2,v_3)$ we have:

$$\begin{align*} (dx)(a,v) &= (dx)((a_1,a_2,a_3),(v_1,v_2,v_3)) \\ {\rm (by \hspace{3pt} linearity...)} &=dx((a_1,a_2,a_3),(v_1i+v_2j+v_3k)) \\ {\rm (by \hspace{3pt} linearity...)} &=dx(a,v_1i)+dx(a,v_2j)+dx(a,v_3k) \\ &= v_1dx(a,i) + v_2dx(a,j) + v_3dx(a,k) \\ &= v_1. \end{align*}$$ That's it!

Similarly, we define: $$\begin{align*} (dy)(a,i)=0, & (dz)(a,i)=0, \\ (dy)(a,j)=1, & (dz)(a,j)=0, \\ (dy)(a,k)=0, & (dz)(a,k)=1, \end{align*}$$ and evaluate them on any $(a,v)$.

These functions are smooth on $a$, as constant functions. Therefore, these are smooth $1$-forms.

Proposition: Every (smooth) $1$-form $\varphi$ on ${\bf R}^3$ can be represented as $\varphi = Adx + Bdy + Cdz$, where $A,B,C \colon {\bf R}^3 \rightarrow {\bf R}^3$ are (smooth) functions.

Proof: We need to find $A$,$B$,$C$ in terms of $\varphi$.

Given $a$, take $i$ at $a$, $i_a$. Define $$\begin{align*} A(a) &= \varphi(a,i_a), \\ B(a) &= \varphi(a,j_a), \\ C(a) &= \varphi(a,k_a). \end{align*}$$

Let $\psi = Adx + Bdy + Cdz$ and show that $\psi = \varphi$. How?

Both should take $(a,v)$ to the same value. So, it suffices to show that for $v = i_a$,$j_a$,$k_a$ (since it's linear on $v$).

$$\begin{align*} \psi(a,i_a) &= (Adx + Bdy + Cdz)(a,i_a) \\ {\rm (linearity)} &= A(a)dx(i_a) + B(a)dy(i_a) + C(a)dz(i_a) \\ &= A(a) \\ &= \varphi(a,i_a) \end{align*}$$ (same for $j$ and $k$). $\blacksquare$

In ${\bf R}^N$ now, a $1$-form is $$\varphi \colon {\bf R}^N \times {\bf R}^N \rightarrow {\bf R},$$ a function (smooth on $1^{\rm st}$ variable and linear on the second variable).

Then every $\varphi$ can be represented as $$\varphi = A_1dx_1 + A_2dx_2 + \ldots + A_N dx_N,$$ where $dx_i$ is a $1$-form with $$dx_i(e_j)=\delta_{ij}$$ ($\{e_j\}$ basis of ${\bf R}^N$).

What about manifolds now?

To take a simplified approach, we assume $M \subset {\bf R}^N$, then $1$-forms on $M$ are simply "restrictions" of $1$-forms on ${\bf R}^N$.

If $\varphi \colon {\bf R}^N \times {\bf R}^N \rightarrow {\bf R}$ and $TM={\bf R}^N \times {\bf R}^N$, then $\varphi |_{TM}$ is the restriction of $\varphi$ on the tangent bundle.

Example: Suppose $N=3$, $M$ is the $(x,y)$-plane.

Then $\varphi \in \Omega^1({\bf R}^3)$ is: $$\varphi = A(x,y,z)dx+B(x,y,z)dy+C(x,y,z)dz.$$

Restrict it to $M$, starting with $dz$: $$dz(e_1)=0, dz(e_2)=0, dz(e_3)=0.$$

Here $e_3 \not\in T_aM = $ horizontal plane. Then, for the restrictions to $M$, we have

$$dz|_M(e_1)=0, dz|_M(e_2)=0.$$

Hence $dz|_M=0.$

Similarly, $$dx|_M(e_1)=1, dx|_M(e_2)=0,$$ $$dy|_M(e_1)=0, dy|_M(e_2)=1.$$

Then $$\varphi|_M=Adx + Bdy.$$

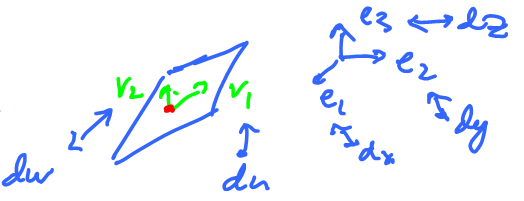
Example: Slightly more complex...

Observe: there are no $dx,dy,dz$; there are $dv,dw$ instead!

We now compute $du$, $dw$ -- via projection.

Example:

Here $M$ is curved. Do same as above for each $T_aM \subset {\bf R}^N$. Note: $$TM \subset T{\bf R}^N.$$