Gauss-Bonnet theorem

The formula is based on the observation that, for a cell complex in the plane, at a given vertex V the sum of the angles between each pair of adjacent edges connecting V to its neighbors is always equal to $2 \pi$.

Then, the Gauss-Bonnet formula is: $$\int\int_MKdV+\int_{\partial M}k_gds=2 \pi \chi(M),$$ where $M$ is a compact two-dimensional Riemannian manifold, $K$ is its Gaussian curvature, $k_g$ is the geodesic curvature along the boundary $\partial M$ of $M$, and $\chi(M)$ is its Euler characteristic.

The discrete case is: $$K(v)=\frac{2 \pi - \sum_u \theta_u}{A_v},$$ where the summation is of the angles over all adjacent vertices $u$ and $A_v$ is the area of the dual cell.

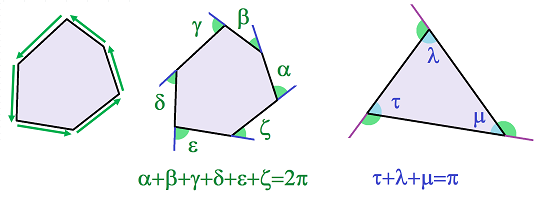
Now, what if $Q$ is a polygon and $V$ is a vector field that follows its edges, counter-clockwise?

Then the rotation of $V$ is the sum of the outer angles of $Q$. Since $\chi (Q) =1$, this sum is equal to $2\pi$. In the case of a triangle, the sum of the inner angles is $3\pi$ minus the former. We have proven a theorem familiar from middle school:

Corollary (Sum of Angles of Triangle). It is equal to $180$ degrees.