This site is being phased out.
The geometry a gray scale image
Contents
The topology graph
The nodes of the topology graph represent all "objects and holes" in the image. In order to avoid ambiguity we require that the topological analysis of the graph satisfy this uniqueness principle:
One obvious answer is to list the tips of the graph as the dark and light objects in the image.
However, this approach ignored the possibility that the geometry of the object may indicate whether a particular object is noise.
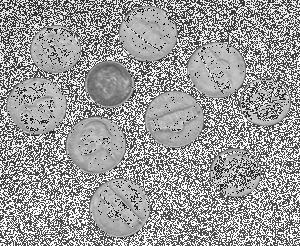
The image on the right has a lot of dark dots. They are meaningless topological features, noise. How need to exclude them from consideration. How?
Boundaries, noise, and geometry
So, what we have captured in the topology graph is all possible topologies of the image!
Even with the uniqueness principle there is still room for ambiguity. If only one of the two is counted, which one? More importantly, which one should be captured, measured, etc? The answer should come from the context. For example, objects that are too small or have too low contrast may be deemed unimportant. They are noise.
Note: There is still some room for ambiguity. Should all objects that aren't noise be counted? No, because some of them may contain other objects. These objects represent the background for other objects.
The noise objects and the background objects are inactive. The rest are active.
We will follow this rule:
- background objects contain active objects,
- active objects contain noise objects,
- only the active ones are counted.
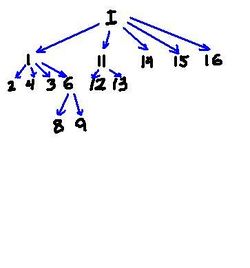
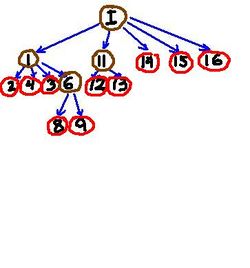
To illustrate consider the image and its topology graph below. It describes the relation between all objects in the image - each object contains the one the arrow point at. 'I' stand for the object which is the whole image. For the sake of simplicity we ignore light objects.
Depending on the noise setting, some of these objects will be
- active (circled with red),
- background (circled with brown), or
- noise (no marking).
Consider the two further examples below.
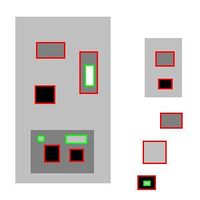
Example: If there are no restrictions (there is no noise), there are $14$ objects - $10$ dark and $4$ light: 10 dark and 4 light active objects:
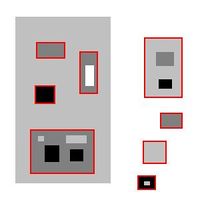
Example: If we decide that everything smaller than say $500$ pixels is noise, we are left with just $8$ dark objects: 8 dark active objects:
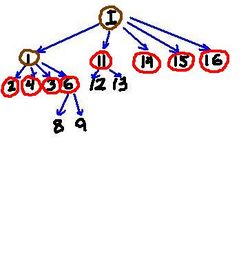
Using the standard terminology of graph theory,
- the whole image object is the root node,
- the noise nodes are found as a collection of sub-trees corresponding to nodes,
- the active nodes are leaf nodes of what's left after noise nodes have been removed,
- the background nodes are the rest.
Exercise. Construct the inclusion tree for light objects in the above image.
Exercise. Is it possible to have two green (light) contours inside each other without a red (dark) one between them?
Note: One might be concerned that the larger gray rectangle should also be counted because it's just another object behind the smaller ones. However, these are 2D images and there is no "behind" in 2D...
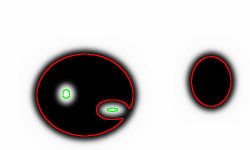
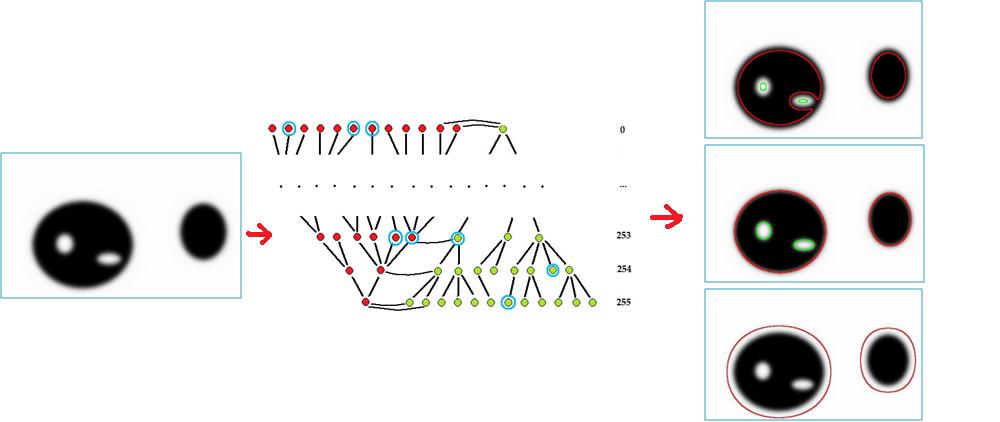
It may seem clear that in the above image there are two objects and the fist one has two holes. However, where the boundaries of these objects are located depends on the chosen threshold or thresholds of their measurements. The choice of these thresholds will affect the topology of the image, as illustrated below.
The topology is simplified.
Exercise. Draw a simplified topology graph for these images.
The analysis algorithm
The algorithm is incremental. The layers are added to the graph one at a time. Each time we increase the threshold for the upper and lower level sets, there are six kinds of events that can (along with their combinations) happen to the connected components of these sets:
- a dark object grows;
- a light object shrinks;
- a dark object appears;
- a dark object forms a hole (a light object) inside;
- two dark objects merge;
- a light object splits.
Just as with binary images, instead of the topology graph we build the augmented topology graph, or simply the augmented graph, of the image. The growing threshold creates a partial order on the set of pixels. In that order, the pixels are added to the image. The procedure of building this graph with nodes representing cycles is exactly the same as the one for binary images as presented above. The frames generate principal cycles and the rest are auxiliary cycles. The topology graph can be extracted from the augmented graph by removing all auxiliary nodes and adding arrows between the principal nodes accordingly.
Outline:
- All pixels in the image are ordered in such a way that all darker pixels come before lighter ones.
- Following this order, each pixel is processed:
- add its vertices, unless those are already present as parts of other pixels;
- add its edges, unless those are already present as parts of other pixels;
- add the face of the pixel.
- At every step, the graph is given a new node and arrows that connect the nodes in order to represent the merging and the splitting of the cycles:
- adding a new vertex creates a new component;
- adding a new edge may connect two components, or create, or split a hole;
- adding the face to the hole eliminates the hole.
- Filter and remove the noise nodes.
- Select the tips of branches (leaves).
Exercise: Suppose the image consists of two adjacent pixels, black and gray, on white background. Then, the construction of the augmented graph is exactly the same as described above. What is the topology graph?
Measuring objects
The the most important characteristic of an object is its area, which is simply the number of pixels. It's also the first measurement of importance of the object. Whatever the "real" (or physical) object is, its area computed this way will be as close as we like to its "true" area as the resolution increases. This is justified by appealing to Lebesgue integral.

The centroid is the center of mass of an object is computed as if this is a lamina with uniform density. Generally, the center of mass is found via computing 3 integrals over the region: the area $M$ and the (first) moments $M_x$ and $M_y$. Then the center of mass has coordinates $(M_y/M,M_x/M)$. Of course, all symmetric figures - squares, rectangles, parallelograms, circles, ellipses etc - have centers of mass in the center.
The perimeter is easy to compute but the result depends on the orientation of the object with respect to the grid. Therefore it is not a good way to measure objects in digital images. The more general issue of measuring lengths of curves is addressed in Lengths of curves.
Roundness $= 4π*area/perimeter^2$.
Then roundness of circle = 1, roundness of a square = .8, elongated objects will have lower roundness.
For the rest, we will use the image below as an example:
The contrast of an object measures how different it is from its background. Simply put, it's max gray level - min gray level of the object. More precise definition is below.
Contrast of a dark object
- = highest gray level adjacent to it - lowest gray level within it
- = highest gray level adjacent to it - object's intensity
Contrast of a light object
- = highest gray level within it - lowest gray level adjacent to it
- = object's intensity - lowest gray level adjacent to it
For example, the intensity of object #12 is $192$ and that of #11 is $128$. Therefore, the contrast of object #12 is $192 - 128 = 64$.
The area/size of an object can be understood as its mass as if this is a lamina with uniform density. However, this approach ignores the gray values of the pixels. In case of a gray scale image we have an alternative. We can treat the gray values as values of the density of the lamina. The total amount of gray, or mass, in the object in comparison to the the surrounding area is the most complete characteristic of its importance. We define
The mass of a dark object
- = the sum of (the gray value of the surrounding area - the gray value of the pixel), over all pixels in it
The massof a light object
- = the sum of (the gray value of the pixel - the gray value of the surrounding area), over all pixels in it
For example, object #11 has $280$ pixels of gray level $0$ (from the black rectangle #13), $567$ pixels of gray level of $128$ (from rectangle #12), and $4984 - 280 - 567 = 4137$ pixels of gray level $192$ (the rest). Since it is surrounded by white ($255$), its the mass is $$280*(255-0) + 567*(255-128) + 4137*(255-192) = 404,040.$$
The center of mass of an object can be understood as if this is a lamina with uniform density. In other words, we ignore the gray values of the pixels. In case of gray level image we have an alternative. We can treat the gray values as values of the density of the lamina. (Exercise.)
The contrast of an object is the maximal difference of its gray level from its background. Roughly, it's max gray level - min gray level of the object. Alternatively one can consider the average instead of max/min. A more precise definition is below.
Average contrast of a dark object
- = the gray value of the surrounding area - average gray level within it
- = the gray value of the surrounding area - object's average intensity
Average contrast of a light object
- = average gray level within it - the gray value of the surrounding area
- = object's average intensity - the gray value of the surrounding area
To provide yet another illustration of the meaning of these characteristics of objects let's consider this analogy.
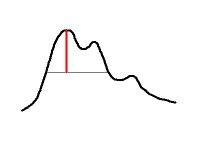
The gray scale function of an image is a function of two variables. It is represented by its graph which is a surface. The objects correspond to maxima (light) and minima (dark) of this function and their combinations.
So, we can think of light objects as mountaintops. More precisely, they are what is removed when the mountaintop is removed;
Now, one can measure these mountaintops and the amount of work done in a number of ways.
One can measure the size of the flat area left after the removal. That's the size or area of the object.
One can measure the depth of the ground that has been removed, or by how much the mountain has become shorter. That's the contrast of the object:
One can measure the amount (volume, mass) of ground that has been removed. That's the mass:
Now, dark objects are valleys... Exercise