Cubical complex

The definition

For objects located in a Euclidean space, we would like to devise a data structure that we can use to first represent and then topologically analyze them.

Suppose the Euclidean space ${\bf R}^N$ is given and so is its cubical grid ${\bf Z}^N$. Suppose also that we have its decomposition ${\mathbb R}^N$, a list of all (closed) cubical cells in our grid.

We defined a cubical complexes as a collection of cubical cells $K\subset {\mathbb R}^N$ for which the boundary operator is well defined. This requires us to include all “faces” of the cells already present.

$N=2:$

$N=3:$

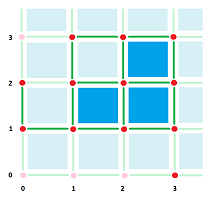
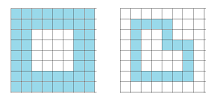
Example. The cubical complex $K$ of the pixel at the origin is given by a list of cells of all dimensions:

• $0: \{0 \} \times \{0 \},\ \{1 \} \times \{0 \},\ \{0 \} \times \{1 \}, \{1 \} \times \{1 \}$;
• $1: \{0 \} \times [0,1],\ [0,1] \times \{0 \},\ [0,1] \times \{1 \},\ \{1 \} \times [0,1]$;
• $2: [0,1] \times [0,1]$.

Now, their boundaries are defined within the complex:

• $\partial \{(0, 0) \} = 0$, etc.,
• $\partial \{0 \} \times [0,1] = \{(0,0) \} + \{(0,1) \}$, etc.,
• $\partial \left( [0,1] \times [0,1]\right) = [0,1] \times \{0 \} + \{0 \} \times [0,1] + [0,1] \times \{1 \} + \{1 \} \times [0,1]$.

$\square$

Note: Cell decomposition of digital images produces cubical complexes. These complexes however are special in the sense that their $1$-cells can only appear as boundaries of its $2$-cells. In general, this is not required.

For $N=3$, we have:

• $0$-cell $\{n \} \times \{m \} \times \{k \}$;
• $1$-cell $\{n \} \times \{m \} \times [k, k + 1]$, or $\{n \} \times [m, m + 1] \times \{k \}$, or $\{n \} \times \{m \} \times [k, k + 1]$;
• $2$-cell $[n, n + 1] \times [m, m + 1] \times \{k \}$, or $\{n \} \times [m, m + 1] \times [k, k + 1]$, or $[n, n + 1] \times \{m \} \times [k, k + 1]$;
• $3$-cell $[n, n + 1] \times [m, m + 1] \times [k, k + 1]$;
• etc.

Exercise. Provide the list representation of the complex of a unit cube.

Recall that, more generally, a cubical cell in the $N$-dimensional space is the product of vertices and edges: $$P := A_1 \times A_2 \times A_3 \times ... \times A_N,$$ where $A_i = [n_i, n_i + 1]$ or $A_i = \{n_i\}$. If the former case happens $m$ times, this cell is an $m$-cube.

The boundary cells, also known as $(m-1)$-faces, of this $m$-cell are certain $(m-1)$-cells that can be computed from the above representation of the cube $P$. For each edge $A_i = [n_i, n_i + 1]$ in the product, we define a pair of opposite faces of $P$: $$P_i^- := B_1 \times B_2 \times B_3 \times ... \times B_N,$$ $$P_i^+ := C_1 \times C_2 \times C_3 \times ... \times C_N,$$ where

• $B_k=C_k=A_k$ for $k \ne i$,
• $B_i=\{n_i\}$, and
• $C_i=\{n_i+1\}$.

Then the list of faces of $P$ is $$\{ P_i^-,P_i^+:A_i = [n_i, n_i + 1],i=1,2,...,N \}.$$ It follows that the total number of $(m-1)$-faces is $2m$.

One can define $k$-faces, $k<m$, of $P$ inductively, as faces of faces.

Exercise. Give a direct construction of (a) $(m-1)$-faces of $m$-cube $P$, (b) all $k$-faces for $k<m$ of $P$. (c) How many of each dimension?

Definition. A cubical complex $K$ is a collection of cubical cells in ${\mathbb R}^N$ for some $N$ satisfying the condition: if a cell belongs to $K$ then so do all of its faces.

Exercise. Define cubical maps in such a way that together with cubical complexes they form a category.

Definition. The dimension $\dim K$ of a cubical complex $K$ is the highest among the dimensions of its cells.

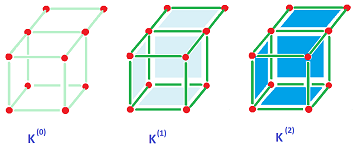
Definition. For a given $n$, the collection of all $k$-cells with $k \le n$ of complex $K$ is called the $n$-skeleton of $K$ denoted by $K^{(n)}$.

The sequence of skeleta can be understood as a blueprint of the complex or even a step-by-step algorithm for building it, from the ground up: $$K^{(0)} \subset K^{(1)} \subset \ ...\ \subset K^{(N-1)} \subset K^{(N)} = K.$$

Exercise. Show that skeleta are also cubical complexes and $\dim K^{(n)} \le n$.

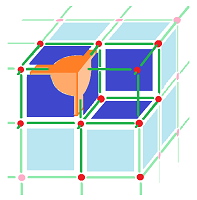
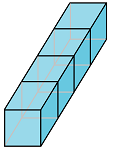
Once the skeleta of the cube are found, we can use them to build new things:

For example, the skeleta of this this solid torus are built from those of the cube:

Just keep in mind that the shared vertices, edges, faces, etc. appear only once.

Exercise. Find the cubical complex representation of the regular, hollow, torus.

Realizations

Recall that a realization of a graph $G$ is a topological space $|G|$ with

• a point for each node of $G$, and
• a path for each edge of $G$ between those points that doesn't intersect the other paths except at the end-points.

This construction looks somewhat similar to that of the $1$-skeleton.

The idea is the same for cubical complexes. A realization of a cubical complex $K$ is a topological space $|K|$ with

• a point for each vertex of $K$, and
• a path for each edge of $K$,
• and so on for all cells of $K$,

put together according to the data encoded in $K$. What makes things so much simpler is the fact that the cells come directly from ${\mathbb R}^N$ and there is only one way to put them together. That's why there is one and only one realization!

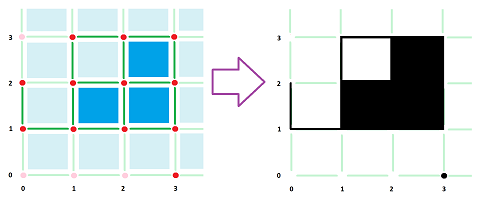
Definition. The union of the cells of a given cubical complex $K$ is called its realization: $$|K|:=\bigcup K.$$

A cubical complex is called finite when it has a finite number of cells. Meanwhile, ${\mathbb R}^N$ is an infinite cubical complex, and $$|{\mathbb R}^N|={\bf R}^N.$$

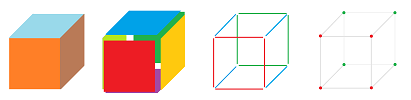
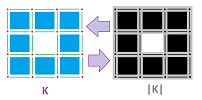
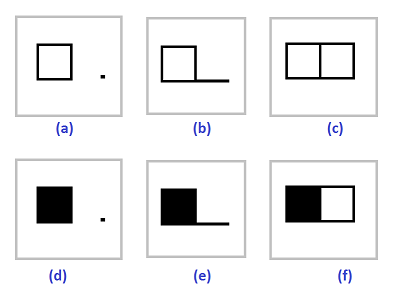
Recall that an open $k$-cell is homeomorphic to ${\bf R}^k$. Both open and closed cells are subsets of the Euclidean space ${\bf R}^N$ and that's where their topology comes from.

The illustration clearly shows that the boundary of the cell is different from the frontier, which is empty for $k$-cells with $k<N$.

These are the “open” cells:

• $0: \{0 \} \times \{0 \}, \{1 \} \times \{0 \}, \{0 \} \times \{1 \}, \{1 \} \times \{1 \}$,
• $1: \{0 \} \times (0,1), (0,1) \times \{0 \}, (0,1) \times \{1 \}, \{1 \} \times (0,1)$,
• $2: (0,1) \times (0,1)$.

Exercise. Show that we can replace “closed” with “open” in the definition of cubical complex and its realization won't change.

It follows then that, even though cells may be open, the realization produced is closed (which is a result of the complex being closed under the boundary operator). The difference is, as you can see, that this latter approach results in a partition of the realization.

Theorem. The realization of a cubical complex is a closed subset of ${\bf R}^N$.

Exercise. The conclusion is obvious for a finite cubical set as the finite unions of its closed cells. What about infinite? Hint: unlike the union of $[-1/n,1/n],\ n>0$, the union of cells doesn't produce new limit points. This kind of collection is called “locally finite” (why?).

Proposition. The realization of a finite cubical complex is bounded.

How do we use cubical complexes? If we want to study the topology of a subset of the Euclidean space, we do that by representing it as a realization of a cubical complex, if possible:

• Given $X \subset {\bf R}^n$, find a cubical complex $K$ such that $|K| = X$, evaluate its homology, then set $H(X) := H(K)$.

In a sense, a complex and its realization are the same:

Indeed, a cubical complex creates a subset of ${\bf R}^N$ via realization but that union of cubical cells can be decomposed in one and only one way producing the same cubical complex. The distinction should still be maintained:

• $K$ is a collection of subsets of the Euclidean space: $K \subset 2^{ {\bf R}^N }$, while
• $|K|$ is a collection of points in the Euclidean space: $|K|\subset {\bf R}^N$.

The deceptively simple idea of realization conceals some difficult issues. To begin with, it is possible that $X = |K| = |L|$ is the realization of either of two different cubical complexes $K,L$ created with two different grids of ${\bf R}^N$:

For our analysis to make sense, we'll have to show that the resulting homology is the same: $H(K) \cong H(L)$. Moreover, the homology groups should be the same for topologically equivalent spaces:

The following statement will be our beacon:

Theorem (Invariance of Homology). Suppose two homeomorphic subsets $X,Y$ of ${\bf R}^N$ are realizations $$X = |K|,\ = |L|$$ of two cubical complexes $K,L$, then they have isomorphic homology groups: $$|K| \approx |L| \Rightarrow H(K) \cong H(L).$$

Exercise. Prove that any tree or any plane graph can be represented as a one-dimensional cubical complex. Give an example of a graph that cannot be represented by a cubical complex.

Exercise. When is a cubical complex in ${\mathbb R}^3$ a surface?

Exercise. Each open cell has Euclidean topology. But is the topology formed on a cubical set as the disjoint union of these cells Euclidean?

The boundary operator

A cubical complex represents a geometric object in a finite form. It is a list of “cells” combined with the information on how they are attached to each other.

Now, a $k$-chain is a combination (a formal sum) of finitely many $k$-cells, such as $a + b + c$.

The boundary operator $\partial$ represents a relation between cells and chains of different dimensions that captures the topology of the cubical complex. We often specify the dimension of the cell involved: $\partial_k(x)$ stands for the boundary of $k$-cell $x$.

Let's review.

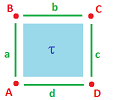
Example.

The boundary of a vertex is empty, so the boundary operator of a $0$-chain is $0$: $$\partial_0 (A) = 0.$$ The boundary of a $1$-cell consists of its two end-points, so we have: $$\partial_1 (a) = \partial (AB) = A +B.$$ The boundary of a $2$-cell consists of its four edges, so we have: $$\partial_2 (\tau) = \partial (ABCD) = a+b+c+d.$$ $\square$

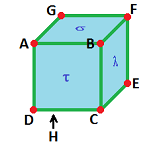
Example.

In dimension $3$, there is only one

• $3$-cell: $\alpha = ABCDEFG.$

Next,

• $2$-cells: $\tau = ABCD,\ \sigma = BCFG,\ \lambda = CFED.$

To compute the boundary of $\alpha$ we need to express its faces in terms of these $2$-cells: $$\begin{array}{llllll} \partial \alpha &= ABCD + BCFG + CDEF + 3 {\rm \hspace{3pt} more} \\ &= \tau + \sigma + \lambda + 3 {\rm \hspace{3pt} more}. \end{array}$$ $\square$

Suppose the ambient dimension $N$ is fixed, as well as the grid of the Euclidean space ${\bf R}^N$ and the “standard cubical complex” ${\mathbb R}^N$ of ${\bf R}^N$. Suppose $K \subset {\mathbb R}^N$ is a cubical complex.

Notation. We denote $C_k=C_k(K)$ the set of all $k$-chains in $K$.

We will call $C_k(K)$, as before, the $k$th chain group of cubical complex $K$.

Theorem. The chain group $C_k(K)$ of $K$ is the subgroup of $C_k=C_k({\mathbb R}^N)$ generated by the $k$-cells in $K$.

Given a $k$-chain $s\in C_k(K)$, $$s = a_1 + a_2 + ... + a_n,$$ where $a_1, a_2, ..., a_n$ are $k$-cells in $K$, the boundary $\partial s$ of $s$ is given by $$\partial s := \partial a_1 + \partial a_2 + ... + \partial a_n.$$

What we know is that the boundaries of $k$-cells are $(k-1)$-chains, and, moreover, the boundaries of $k$-chains are $(k-1)$-chains as well. Now, since $K$ is a cubical complex, if $K$ contains a cell $s$, it also contains all of $s$'s faces. Therefore, $$s\in K\Rightarrow \partial s\in C_k(K),$$ and $$s\in C_k(K) \Rightarrow \partial s\in C_k(K).$$ So, the restrictions of the boundary operators that we defined for the whole space are now the boundary operators of $K$! They are $$\partial ^K_k := \partial_k \Big|_{C_k(K)}:C_{k}(K) \to C_{k-1}(K),\ k=0,1,2....$$ We use the same notation, $\partial$, for these functions, whenever possible.

Since this is a restriction of a homomorphism to a subgroup, we have the following.

Theorem. The boundary operator is a homomorphism.

Moreover, it follows that the main property,

every boundary is a cycle,

of the boundary operator remains true for this restriction.

Theorem (Double Boundary). The composition of two boundary operators $$\partial _{k}\partial _{k+1}:C_{k+1}(K) \to C_{k-1}(K),\ k=1,2,3...$$ is zero. Or, simply put: $$\partial \partial = 0.$$

Example. As an illustration, consider this example of two operators below. Neither operator is $0$, but their composition is:

Here,

• $A$ is the projection on the $xy$-plane, which isn't $0$;
• $B$ is the projection on the $z$-axis, which isn't $0$;
• $BA$ is $0$.

$\square$

The chain complex

The rest of the definitions from the last section also apply.

Definition. For a given $k=0,1,2,3...$,

• the $k$th cycle group of $K$ is the subgroup of $C_k(K)$ defined by:

$$Z_k=Z_k(K):=\ker \partial_k;$$

• the $k$th boundary group of $K$ is the subgroup of $C_k(K)$ defined by:

$$B_k=B_k(K):=\operatorname{Im} \partial_{k+1}.$$

This is how they are visualized:

As before, the big picture of the algebra of chains and their boundaries is given by the chain complex of the cubical complex $K$ (an unfortunate reuse of the word “complex”): $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccccccccc} ...& \ra{\partial_{k+2}} & C_{k+1}(K)& \ra{\partial_{k+1}} & C_{k}(K)& \ra{\partial_{k}} & C_{k-1}(K) & \ra{\partial_{k-1}} & ... & \ra{\partial_{1}} & C_{1}(K)& \ra{\partial_{0}} & 0. \end{array} $$ Remember, it is the property $\partial\partial =0$ what makes this sequence a chain complex.

Corollary. For any cubical complex $K$, $$B_k(K)\subset Z_k(K),\ \forall k=0,1,2,...$$

That's what makes defining homology groups possible.

Definition. The $k$th homology group, $k=0,1,2,3...$, of a cubical complex $K$ is given by $$H_k(K):=Z_k(K) / B_k(K).$$

For a given $k$, the part of the chain complex that affects $Z_k,B_k,H_k$ is often illustrated by this diagram:

Then, $H_k$ captures the difference between $Z_k$ and $B_k$.

Exercise. Prove that $$H_m(K)=H_m(K^{(m+1)}),$$ where $K^{(m+1)}$ is the $(m+1)$-skeleton of $K$. Give an example that shows that replacing $K^{(m+1)}$ with $K^{(m)}$ fails.

For reference we will need the following classification theorem.

Theorem (Fundamental Theorem of Finitely Generated Abelian Groups). Every finitely generated abelian group $G$ is isomorphic to a direct sum of primary cyclic groups and infinite cyclic groups: $${\bf Z}^n \oplus {\bf Z}_{q_1} \oplus ... \oplus {\bf Z}_{q_s},$$ where $n \ge 0$ is the rank of $G$ and the numbers $q_1,...,q_s$ are powers of (not necessarily distinct) prime numbers. Here ${\bf Z}^n$ is the free part and the rest is the torsion part of $G$.

Proposition. For a finite cubical complex $K$, the groups $$C_k(K),Z_k(K),B_k(K),H_k(K)$$ are direct sums of finitely many copies of ${\bf Z}_2$: $${\bf Z}_2 \oplus {\bf Z}_2 \oplus ... \oplus {\bf Z}_2 .$$

Exercise. Prove the proposition. Hint: what is the order of the elements?

The number of the factors in such a group $G$ is also the number of linearly independent generators. That's why, for the rest of this section, we will refer to this number as the dimension $\dim G$ of the group (after all it is a vector space over ${\bf Z}_2$).

Exercise. Find the formula for $\dim G$ in terms of the size (the number of elements) $\# G$ of $G$.

Definition. The dimension of $H_k(K)$ is the number of topological features in $K$ of dimension $k$, the $k$th Betti number: $$\beta _k:=\dim H_k(K).$$

Meanwhile, the reduced homology groups $\tilde{H}_k(K)$ of complex $K$ are defined via the identical formulas but applied to the augmented chain complex: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccccccccc} ...& \ra{\partial_{k}} & C_{k-1}(K) & \ra{\partial_{k-1}} & ... & \ra{\partial_{1}} & C_{1}(K)& \ra{\epsilon} & {\bf Z}_2 &\ra{0} & 0,. \end{array} $$ where $\epsilon$ is given by: $$\epsilon (r_1c_1+...+r_nc_n):=r_1+...+r_n, \ r_i\in {\bf Z}_2.$$ Then, in particular, $$\tilde{H}_k(K) = H_k(K), \ k=1,2,...,$$ but $$\dim \tilde{H}_0(K) =\dim H_k(K) -1.$$

Examples

All these groups can be represented as lists!

Indeed, $C_k(K)$ is generated by the finite set of $k$-cells in $K$ and $Z_k(K),B_k(K)$ are its subgroups. Therefore, they all have only finite number of elements. Meanwhile, their quotient $H_k(K)$ lists the cosets, so homology is a list of lists.

These lists can be accompanied by illustrations, for small enough cubical complexes, with each cell in those lists shown. However, below, we will intentionally ignore the pictures -- as soon as the chain complex is found. The goal is to demonstrate that the second step -- computing $Z_k(K),B_k(K),H_k(K)$ -- is purely algebraic.

We will start with these three, progressing from the simplest to more complex, in order to reuse our computations:

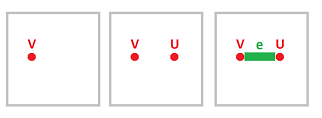
Example 1 (single vertex). Let $K:=\{V\}$. Then $$\begin{array}{lll} C_0&=< V > &=\{0,V\},\\ C_i& &=0, \quad\forall i>0. \end{array}$$ Then we have the whole chain complex here: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccccccccc} 0 & \ra{\partial_{2}=0} & C_{1}=0& \ra{\partial_{1}=0} & C_{0} =< V > & \ra{\partial_{0}=0} & 0. \end{array} $$ From this complex, working algebraically, we deduce: $$\begin{array}{lllllll} Z_0:=&\ker \partial _0 &= < V > &=\{0,V\},\\ B_0:=&\operatorname{Im} \partial _1 & &=0. \end{array}$$ Therefore, $$H_0:=Z_0 / B_0=< V > / 0= < [V] > =\{ [0],[V]\}=\{\{0\},\{V\}\},$$ and $\dim H_0=1$, i.e., $K$ has a single path-component. Also, $$H_i=0,\ \forall i>0,$$ so no holes.

$\square$

Example 2 (two vertices). Let $K:=\{V, U\}$. We copy Example 1 and make small corrections: $$\begin{array}{llllll} C_0&=< V,U > &=\{0,V,U,V+U\},\\ C_i& &=0, \quad\forall i>0. \end{array}$$ Then we have the whole chain complex here: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccccccccc} 0 & \ra{\partial_{2}=0} & C_{1}=0 & \ra{\partial_{1}=0} & C_{0} =< V,U > & \ra{\partial_{0}=0} & 0. \end{array} $$ Now using only algebra, we deduce: $$\begin{array}{llllll} Z_0:=&\ker \partial _0 &= < V,U > &=\{0,V,U,V+U\},\\ B_0:=&\operatorname{Im} \partial _1 & &=0. \end{array}$$ Therefore, $$\begin{array}{llllll} H_0:=&Z_0 / B_0&=< V,U > / 0&= < [V],[U] > \\ &=\{ [0],[V],[U],[V+U]\}&=\{\{0\},\{V\},\{U\},\{V+U\}\}. \end{array}$$ So, since the dimension of this group is $2$, $K$ has two path-components. Also, $$H_i=0,\ \forall i>0,$$ so no holes.

$\square$

Example 3 (two vertices and an edge). Let $K:=\{V, U, e\}$. We copy Example 2 and make some corrections: $$\begin{array}{llllll} C_0&=< V,U >&=\{0,V,U,V+U\},\\ C_1&=< e >&=\{0,e\},\\ C_i&=0, \forall i>1. \end{array}$$ Then we have the whole chain complex shown: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccccccccc} 0 & \ra{\partial_{2}=0} & C_{1}=< e >& \ra{\partial_{1}=?} & C_{0} =< V,U > & \ra{\partial_{0}=0} & 0. \end{array} $$ First we compute the boundary operator. Consider $$\partial _1 (e)=V+U.$$ Therefore, $$\partial _1 =[1,1]^T.$$ Now the groups.

Dimension $0$ (no change in the first line): $$\begin{array}{llllll} Z_0:=&\ker \partial _0 &= < V,U >&=\{0,V,U,V+U\},\\ B_0:=&\operatorname{Im} \partial _1 &=< V+U >&=\{0,V+U\}. \end{array}$$ Notice the inexactness of our chain complex: $Z_0 \ne B_0$ (not every cycle is a boundary!). It follows, $$H_0:=Z_0 / B_0=< V,U > / < V+U >= < [V] > =\{ \{0,V+U\},\{V,U\}\}.$$ So, since the dimension of this group is $1$, $K$ has one component.

Dimension $1$: $$\begin{array}{llllll} Z_1:=&\ker \partial _1 &= 0,\\ B_1:=&\operatorname{Im} \partial _2 &=0, \end{array}$$ therefore $$H_1= 0/0=0.$$ Still no holes.

$\square$

The transition from Example 2 to Example 3 illustrates how a $0$-cycle can be “killed” by adding a new edge. Let's consider this idea in more generality.

Theorem. Suppose $K$ is a cubical complex and suppose $L=K\cup \{e\}$, where $e\not\in K$ is an edge, is another. Suppose $e=UV$, where $U,V$ are two vertices of $K$. Then there are two cases:

• Case 1: $U \sim V$ in $K$, then
• $\diamond$ $\dim H_0(K) = \dim H_0(L)$ (no new $0$-boundaries),
• $\diamond$ $\dim H_0(K)+1 = \dim H_0(L)$ (a new $1$-cycle);
• Case 2: $U \not\sim V$ in $K$, then
• $\diamond$ $\dim H_0(K) -1 = \dim H_0(L)$ (a new $0$-boundary),
• $\diamond$ $\dim H_0(K) = \dim H_0(L)$ (no new $1$-cycles).

Exercise. Provide details for the above theorem.

Two, slightly more complex, examples:

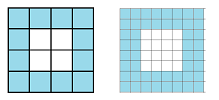
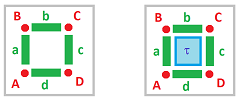
Example 4 (hollow square). Let $K:=\{A, B,C,D, a,b,c,d\}$. Then we have (too many cells to list all elements): $$\begin{array}{llllll} C_0&=< A,B,C,D >,\\ C_1&=< a,b,c,d >,\\ C_i&=0, \quad\forall i>1. \end{array}$$ Note: we think of these two lists of generators as ordered bases.

We have the chain complex below: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccccccccc} 0 & \ra{\partial_{2}=0} & C_{1}=< a,b,c,d > & \ra{\partial_{1}=?} & C_{0} =< A,B,C,D > & \ra{\partial_{0}=0} & 0. \end{array} $$ First we compute the boundary operator. Consider $$\begin{array}{llllll} \partial _1 (a)&=A+B,\\ \partial _1 (b)&=B+C,\\ \partial _1 (c)&=C+D,\\ \partial _1 (d)&=D+A. \end{array}$$ Therefore, $$\partial _1 =\left[ \begin{array}{ccccccccccccc} 1,&0,&0,&1\\ 1,&1,&0,&0\\ 0,&1,&1,&0\\ 0,&0,&1,&1 \end{array} \right].$$ The chain complex has been found, now the groups.

Dimension $0$: $$\begin{array}{llllll} Z_0:=&C_0 & &= < A,B,C,D >,\\ B_0:=&\operatorname{Im} \partial _1 &=< A+B,B+C,C+D,D+A > &=< A+B,B+C,C+D > \end{array}$$ (since $D+A$ is the sum of the rest of them). It follows, $$\begin{array}{lll} H_0:=&Z_0 / B_0&=< A,B,C,D > /< A+B,B+C,C+D > \\ &= < [A] > &=\{B_0,\{A,B,C,D\}\}. \end{array}$$ So, since the dimension of this group is $1$, $K$ has one path-component.

Dimension $1$: $$\begin{array}{llllll} Z_1:=&\ker \partial _1 &= ?,\\ B_1:=&\operatorname{Im} \partial _1 &=0. \end{array}$$ To find the kernel, we need to find all $e=(x,y,z,u)^T\in C_1$ such that $\partial _1 e=0$. That's a (homogeneous) system of linear equations: $$\left\{ \begin{array}{ccccccccccccc} x & & &+u &=0,\\ x &+y & & &=0,\\ & y & +z& &=0,\\ & & z &+u &=0. \end{array} \right .$$ Solving from bottom to the top: $$z=-u \Rightarrow y=u \Rightarrow x=-u,$$ so $e=(-u,u,u,-u)^T,\ u\in {\bf R}$. Then, as signs don't matter, $$Z_1=< e >=<(1,1,1,1)^T>=<a+b+c+d>.$$ Therefore $$H_1= Z_1/0=<[a+b+c+d]>.$$ There is a hole!

$\square$

Example 5 (solid square). Let $K:=\{A, B,C,D, a,b,c,d, \tau \}$. We copy Example 4 and make some corrections. We have (too many cells to list all elements): $$\begin{array}{llllll} C_0&=< A,B,C,D >,\\ C_1&=< a,b,c,d >,\\ C_2&=<\tau>,\\ C_i&=0, \quad\forall i>2. \end{array}$$ We have the chain complex: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccccccccc} 0 & \ra{\partial_{3}=0} & C_{2}=<\tau >&\ra{\partial_{2}=?} & C_{1}=< a,b,c,d > & \ra{\partial_{1}} & C_{0} =< A,B,C,D >& \ra{\partial_{0}=0} & 0. \end{array} $$ First we compute the boundary operator. Consider $$\partial _2 (\tau)=a+b+c+d,$$ therefore, $$\partial _2 =[1,1,1,1]^T.$$ As $\partial _1$ is already known, the chain complex has been found. Now the groups:

Dimension $0$. Since the changes in the chain complex don't affect these groups, we have answers ready: $$\begin{array}{llllll} Z_0:=&C_0 &= < A,B,C,D >,\\ B_0:=&\operatorname{Im} \partial _1 &=< A+B,B+C,C+D >,\\ H_0= &< [A] > &=\{B_0,\{A,B,C,D\}\}. \end{array}$$ So, again, $K$ has one component.

Dimension $1$ (no change in the first line): $$\begin{array}{llllll} Z_1:=&\ker \partial _1 & &= <a+b+c+d>,\\ B_1:=&\operatorname{Im} \partial _1 &=< \partial _2(\tau) > &=<a+b+c+d>. \end{array}$$ Therefore, $$H_1= 0.$$ There is no hole!

$\square$

Exercise. Represent the sets below as realizations of cubical complexes. For each of them:

• (a) find the chain groups and find the boundary operator as a matrix;
• (b) using only part (a) and algebra, find $Z_k,B_k,H_k$ for all $k$, including the generators. (The point is to demonstrate that you understand the algebra.)

Exercise. Compute the homology of a “train” with $n$ cars:

Using spreadsheets to compute boundaries

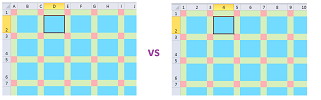
Cells on the plane can be presented in a spreadsheet such as Excel. Below, some of the rows and columns are narrowed in order to emphasize the $1$-dimensional nature of the edges and the $0$-dimensional nature of the vertices:

The cells are represented:

• left: in the standard style, and
• right: in the R1C1 reference style.

The highlighted cell is given by

• D2, and
• R2C4,

respectively. The latter is clearly more mathematical and that's the one we will use. Notice, however, that the coordinate axes go down and right as in a matrix, instead of right and up as we are used to in the Cartesian system.

Also, the coordinates differ from those in the above discussion by a factor of two: the highlighted cell is located at $(1,2)$. Then

• $0$-cells are $(odd,odd)$,
• $1$-cells are $(odd,even)$ and $(even,odd)$,
• $2$-cells are $(even,even)$.

The chains are encoded by putting $0$s and $1$s in all cells. In the former case, the cell is white and the number is invisible while in the latter case, the cell is colored according to its dimension.

Next, we implement the boundary operator.

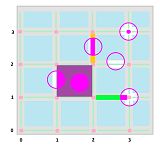
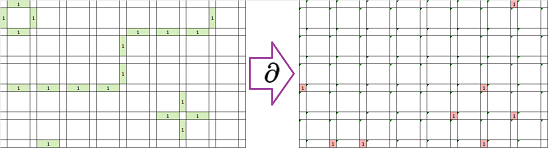
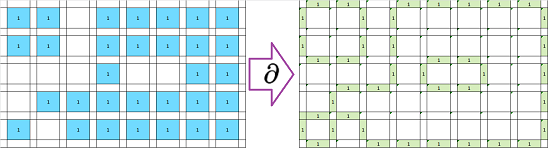
These are the results of computing boundaries, for a $1$-chain:

and a $2$-chain:

The approach to the algorithm for computing the boundary operator is very different from the algebra we have done. Compare the following.

• Normally, to compute the boundary of a $k$-chain, we compute the boundary of each of its $k$-cells as the sum of this cell's boundary cells (dimension $k-1$), add them, and then cancel the repetitions.
• Now, we look at each $(k-1)$-cell present in the spreadsheet, add the values of the $k$-cells of the chain adjacent to it, and then find out whether the result makes this cell a part of the boundary of the chain.

The results are of course the same.

The code is very simple.

Dimension $0$: For each vertex, we compute the sum, modulo $2$, of the values at the four edges adjacent to it:

• =MOD(RC[-21]+R[-1]C[-20]+RC[-19]+R[1]C[-20],2),

and the result is placed on the right. Then,

• if the curve isn't there, we have $0+0+0+0=0$;
• if the curve is passing by once, we have $1+0+1+0=0$;
• if the curve is passing by twice, we have $1+1+1+1=0$;
• if the curve ends here, we have $1+0+0+0=1$.

Dimension $1$: For each edge, we, similarly, compute the sum of the values at the two adjacent faces; horizontal:

• =MOD(R[-1]C[-20]+R[1]C[-20],2);

and vertical:

• =MOD(RC[-21]+RC[-19],2).

Then,

• if the edge is away from the region, we have $0+0=0$;
• if the edge is inside the region, we have $1+1=0$;
• if the edge is on the boundary of the region, we have $1+0=1$.

Link to the file: Spreadsheets.

Exercise. Modify the code to compute the homology groups of graphs on the grid.

Exercise. Devise and implement a similar algorithm for $3$-chains. Hint: use the "sheets" as layers.