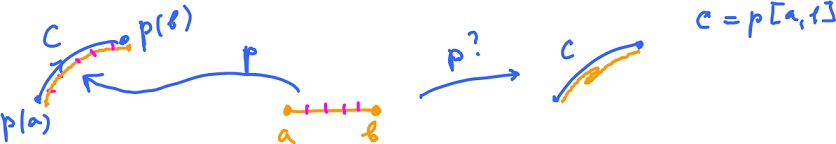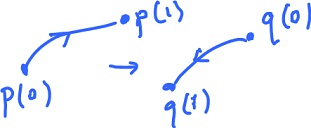Orientation

Orientation of curves

Question: What happens to the displacement when the motion changes direction?

Answer: It changes its sign.

In terms of integrals:

$$\int_a^b V(x) dx = - \int_b^a V(x) dx,$$ where $V$ is the velocity.

This is where it comes from: $$\int_{-[a,b]} f(x) dx = - \int_{[a,b]} f(x) dx = \int_{[b,a]} f(x) dx.$$

Note: There is a difference when you treat the domain of integration as

• an interval: $[ a, b ] = [ b, a ]$;

or as

• an oriented interval: $[ a, b ] = -[ b, a ]$.

More generally, $$\int_{-A} f(x) dx = - \int_A f(x) dx.$$

This may be the flow integral, for example.

The orientation of a curve comes from its parametrization (see Parametric curves). Given a continuous function $$p: [ a, b ] \rightarrow {\bf R}^n,$$ the set $C = p( [ a, b ] )$ is a curve.

Consider a curve given by $p:[0,1] \rightarrow R$. Then $q:[0,1] \rightarrow R$ given by $$q(s) = p(1 - s)$$ is another parametrization that produces the opposite orientation to the one from $p$.

For the curves in the picture there are two possible orientations (and infinite many parametrizations).

Orientation of surfaces

Suppose we want to compute the flow of liquid through a region in space. For that we need to understand the direction of the flow with respect to the orientation of the surface it passes through. There are two ways to do specify the orientation:

1. orient the curve that bounds the region and then use the "screw rule" to find the corresponding normal vector to the surface; and
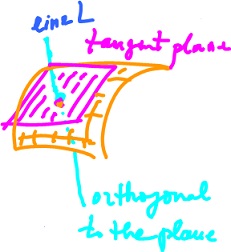
2. look at the tangent plane to the surface and deal with its orientation which is simply a choice of the normal vector.

We can approach the orientation of surfaces in a similar manner to curves. Indeed, the orientation of a surface comes from its parametrization (at least locally).

Let's understand orientation of the square, $Q$, in space first. We can still look at it as corresponding to the direction of the parametric curve (a closed curve!) that bounds the square. This is a more direct way.

Parametrize $Q$ as a map from the unit square in the plane to the $3$-dimensional space: $$R : {\bf R}^2 \rightarrow {\bf R}^3,$$ specifically:

• $R_1(s,t) = s$,
• $R_2(s,t) = t$,
• $R_3(s,t) = 0$.

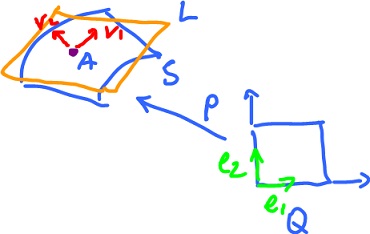
What is its orientation? It is a unit vector perpendicular to both $R(e_1)$ and $R(e_2)$, where $e_1, e_2$ are the (fixed) basis vectors of ${\bf R}^2$. So, if $L$ is a line perpendicular to the square (or a surface), then the orientation is a basis for $L$ with unit vectors. And there are exactly two choices.

Note: the alternative parametrization of $Q$ gives the opposite orientation:

• $R_1(s,t) = 1 - s$,
• $R_2(s,t) = t$,
• $R_3(s,t) = 0$.

The orientation of a surface is determined by the orientation of its tangent plane (hyperplane) $L$. The set of all vectors perpendicular to $L$ is a vector subspace of dimension $1$. There are two possible unit vectors in it. Choosing one of them amount to fixing the orientation.

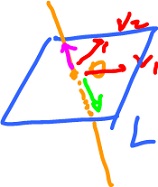
In the special case of $n = 3$, how do we find these vectors? With the cross product.

Given a basis of $L$, say $v_1$ and $v_2$, we take as unit vector $u$, defined as $$u = \frac{v_1 \times v_2}{|| v_1 \times v_2 ||}.$$

Where does the basis of $L$ come from? From the parametrization. Given $$p( 0, 0 ) = A,$$ find $$v_1 = ?$$ $$v_2 = ?$$

To summarize, the basis $\{ v_1, v_2 \}$ comes from that of $R^2$ by means of $p$: $$v_1 = p'( 0, 0 ) e_1,$$ $$v_2 = p'( 0, 0 ) e_2.$$

It should become clear now that what we are talking about here is equivalence classes of parametrizations (or, more generally, atlases) given by:

the Jacobian of the transition map has positive sign.

Orientation of simplices

On the other hand, there are two equivalence classes of orderings of any set, in particular on the set of vertices of a simplex, as follows:

two orderings are equivalent if they differ by an even permutation.

(Recall, even permutation is the composition of an even number of transpositions.)

For example, $ABC$

• isn't equivalent to $ACB$ (one flip), but
• is equivalent to $CAB$ (two flips).