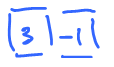Integration of differential forms of degree 2

Higher order forms

Just as $1$-forms are linear functions, $k$-forms as multi-linear functions.

A familiar $1$-linear function is addition: $$+(\lambda \cdot (a, b)) = +(\lambda \cdot a,\lambda \cdot b)= \lambda \cdot +(a,b).$$ It is linear in $(a,b)$.

A familiar $2$-linear function is multiplication: $$\times(\lambda \cdot a,b)) = \lambda \cdot \times(a,b)$$ It is linear in either of the two arguments but not linear in $(a,b)$: $$\times(\lambda \cdot (a,b)) = \lambda ^2\cdot \times(a,b)$$

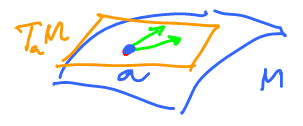
Definition: Given an oriented manifold $M \subset {\bf R}^N$, a differential form of degree $k$, or simply, a $k$-form, $\varphi$ is a function that takes a point $a \in M$ and $k$ vectors in $ \in T_aM$ and finds a real number in ${\bf R}$, and it is differentiable with respect to $a$ and linear with respect of each of the vectors $v$.

As an example, in the familiar $2$-form $dxdy$, $dx$ and $dy$ are the two vectors.

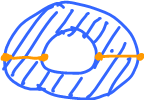
Example: This is a $2$-manifold and that's where a $2$-form is defined:

Required:

• $\varphi$ is $C^m$ with respect to $a \in M$ and
• $\varphi$ is multilinear with respect to $(T_aM)^k$.

Now we simply follow what we did for $1$-forms.

The main step is: all forms are inherited by $M$ from ${\bf R}^N$.

Indeed, if $M \subset {\bf R}^N$, then $TM \subset T{\bf R}^N$. So, if $\varphi$ is a $k$-form on ${\bf R}^N$, $$\varphi \colon {\bf R}^N \times ({\bf R}^N)^k \rightarrow {\bf R},$$ then consider its restriction to $M \colon _c{\bf R}^N$:

• $\varphi$ is defined for each
  • $a \in M$ and
  • $v_1, \ldots, v_k \in T_aM \subset {\bf R}^N.$

That's a $k$-form on $M$, but it's still a form on the whole space and satisfies all the conditions.

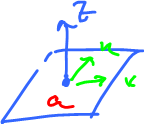
Example: Let's choose $M$ a linear subspace here:

• $N=3$,
• $n=2$,
• $M = \{ (x,y,z): z=0\}$, and
• $a \in M \subset {\bf R}^3$,
• $u,v \in T_aM \subset T_a{\bf R}^3$.

Then the computation is easy. $\blacksquare$

Now, let's consider $2$-forms in ${\bf R}^3$.

Example: What is $dx \hspace{1pt} dy$, in ${\bf R}^3$?

This one does not depend on $a$, the location, only on the tangent vectors. So,

• $(dx \hspace{1pt} dy)(u,v,w) = ?$

Note: One should interpret $(dx \hspace{1pt} dy)$ as name of the form and $(u,v,w)$ as the inputs.

Look at the basis only, then expand by linearity:

$$\begin{align*} (dx \hspace{1pt} dy)(i,j,0)=1\\ (dx \hspace{1pt} dy)(0,j,k)=0\\ (dx \hspace{1pt} dy)(i,0,k)=0. \end{align*}$$

...and by anti-symmetry: $$(dy \hspace{1pt} dx)(j,i,0)=1.$$

Similar for $dy \hspace{1pt} dz$, $dz \hspace{1pt} dx$. $\blacksquare$

Now, the rest of the $2$-forms are "linear combinations" of the basic ones.

Generally, a 2-form in ${\bf R}^3$ looks like this: $$\varphi = Adx \hspace{1pt} dy + Bdy \hspace{1pt} dz + Cdz \hspace{1pt} dx,$$ where $A$, $B$, $C$ are functions $\colon {\bf R}^3 \rightarrow {\bf R}$.

Now, $3$-forms in ${\bf R}^3$.

This is all we need to know:

• $(dx \hspace{1pt} dy \hspace{1pt} dz)(i,j,k)=1$, and
• $=0$ elsewhere.

The rest is found by adding a coefficient function $$\varphi = Adx \hspace{1pt} dy \hspace{1pt} dz ,$$ and anti-symmetry.

For $n$-forms in ${\bf R}^N$, same idea.

For each combination of $n$ variables $$x_{i_1},\ldots,x_{i_n}$$ we have an $n$-form: $$dx_{i_1}\ldots dx_{i_n}.$$ And the form is defined by setting $$(dx_{i_1}\ldots dx_{i_n})(e_{i_1},\ldots,e_{i_n})=1$$ and $0$ elsewhere. The rest a linear combinations of these.

Exercises: Compute forms...

What about discrete forms?

No need for tangents, as we use cochains, i.e., functions: $k$-cells $\rightarrow$ numbers.

Discrete exterior calculus has all the theorems of smooth calculus. Use them.

Integration of $2$-forms

What is the integral of a $2$-form? $$\displaystyle\int_R \varphi^2 = ?$$ Here we suppose that $\varphi$ is a $2$-form in ${\bf R}^2$, $R \subset {\bf R}^2$ is a region with piecewise smooth boundary.

Recall something from calc 3:

• A double integral is computed as an "iterated integral" (Fubini's theorem).

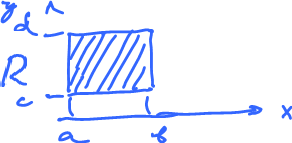
Case 1: $R$ is a rectangle $$\displaystyle\int_R A(x,y)dx \hspace{1pt} dy = \displaystyle\int_c^d\int_a^b A(x,y) dx \hspace{1pt} dy.$$

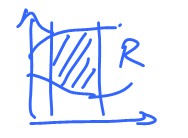
Case 2: Or for a more complicated $R$: between two graphs of $y=f(x)$ and $y=g(x)$ or $x=f(y)$ and $x=g(y)$:

Same idea...

Case 3: Or cut into these pieces, each looks like case 2.

Now we can use this for the following...

What is $\displaystyle\int_S \varphi$, where $S \subset {\bf R}^3$ is a surface?

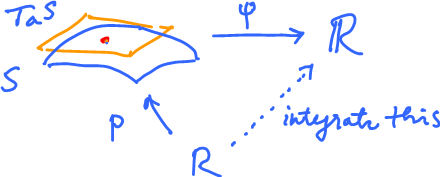
We start with a simple case of $S$ a single patch: $p \colon R \rightarrow S$, where $R$ is a closed rectangle.

Idea: express $\displaystyle\int_S \varphi$ in terms of $\displaystyle\int_R$.

Just like with $1$-forms: if curve $C$ is parametrized by function $p$ then $$\displaystyle\int_C \varphi ^1 = \displaystyle\int_{[a,b]} \varphi(p,p')dt.$$

Consider the diagram:

Or more precisely: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{rllll} TS & \ra{\varphi} & {\bf R} \\ (p,p') \nwarrow & & \nearrow {\rm integral} \\ & R \end{array} $$

Conclusion: To compute $\displaystyle\int \varphi$, integrate the composition over the rectangle.

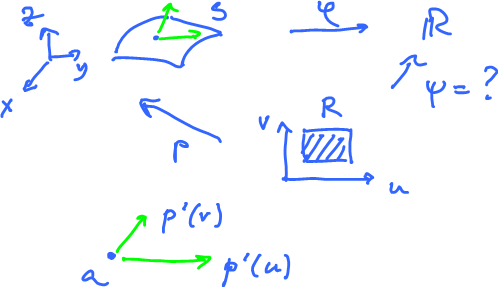
Note: Here we have $S = p(R)$, a single patch, where $p$ is a diffeomorphism. Then we have $$TR \stackrel{(p,p')}{\rightarrow} TS,$$ a map between the tangent bundles.

So, $p$ takes care of the location, $p'$ of the tangents:

Here $p'(v)$,$p'(u) \in T_aS$.

Define $$\psi(u,v) = \varphi(p'(v),p'(u)).$$ Then define the integral of the $2$-form $\varphi$ over a surface $S \subset {\bf R}^3$ by $$\displaystyle\int_S \varphi = \stackrel{+}{-} \displaystyle\int_R \psi,$$ where we take the $+$ if $S$ and $p(R)$ have matched orientations and $-$ if they are opposite.

Further, if $S$ is a compact $2$-manifold, then $$\displaystyle\int_S \varphi = \displaystyle\sum_{i=1}^m \displaystyle\int_{s_i} \varphi,$$ where $s_1, \ldots, s_m$ are the "tiles" of $S$:

• $S = \displaystyle\cup_{i=1}^n s_i$,
• each $s_i$ is covered by single patch,
• ${\rm int} S_i \cap {\rm int} S_j = \emptyset$ if $i \neq j$.

Properties:

• $(1)$ $\displaystyle\int_{-M} \varphi = -\displaystyle\int_M \varphi$.
• $(2)$ $\displaystyle\int_M \varphi$, where $S$ is a oriented manifold, is independent from the parametrization of $M$.

Proof. Plan: Tile-by-tile. Use the change of variables formula, same as for $n=1$. $\blacksquare$

How do we anti-differentiate forms?

We should be able to find the antiderivative of a given form, in the sense of the operation inverse to differentiation, in our case the exterior derivative.

• $n=1$: we know.

If $\varphi$ is a $1$-form, then define $$f(x) = \displaystyle\int_A^x \varphi.$$ Then $$df=\varphi.$$ That's the Fundamental Theorem of Calculus.

• $n=2$: unclear.

We will have to develop some background first, i.e., the Stokes Theorem.

The idea is easier to illustrate for discrete forms.

Recall that integration of discrete forms is simply summation.

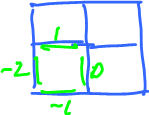
Example: Let $\varphi^1 = $

and let this be our oriented manifold (a curve):

Then $\displaystyle\int_C \varphi^1$ = summation of the values of $\varphi^1$ over all 1-cells, with the sign depending on the orientation of the cell: $$\displaystyle\int_C \varphi^1 = 6+5+1-3-0-1=8.$$ For our grid the orientations of the squares are always chosen to be along the axes.

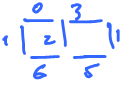
Example: Let $\varphi^2 = $

and let this be our oriented $2$-manifold (with boundary):

Then $$\displaystyle\int_R \varphi^2 = 3 + (-1) = 2.$$

We have had the regions of integration as collections (with repetition allowed) of cells. These "regions" are called chains.

Let's recall what we mean by algebra of chains and cochains.

Chain is a "formal" linear combination of cells of the same dimension, like this: $$3a_1+5a_2-3a_3,$$ etc.

This is a vector space, $C_k(R)$, with $k$-cells serving as a basis.

Assume $R$ is bounded and there are $s$ $k$-cells, then $\dim C_k(R) = s$.

Cochains are linear functionals defined on chains, and it suffices to define them of cells as the basis of the vector space, like this:

$\varphi^1=$

Here $\varphi^1 \colon C_1(R) \rightarrow {\bf R}$ is linear, extended by linearity.

Cochains also form a vector space, $C^k(R)$.

We observe that $$\dim C^k(R)=\dim C_k(R).$$ They have the same dimension!

Indeed, say

• $a_1,\ldots,a_s$ are the $k$-cells, basis of $C_k(R)$ and
• $\varphi_1,\ldots,\varphi_s$ are the $k$-cochains, defined by
  • $\varphi_i(a_j)=\delta_{ij}$.

That's a basis of $C^k(R)$.

This gives us an isomorphism $\lambda \colon C^k(R) \rightarrow C_k(R)$.

So $C^k(R)$ is the dual space of $C_k(R)$.

Coordinatewise, suppose

• $a \in C_k(R)$, $a=(q_1,\ldots,q_s)$ is a chain.

What's the corresponding cochain, $\lambda(a)$? This:

• $\varphi \in C^k(R)$, $\varphi = (q_1,\ldots,q_s)^T$.

Same vector; you just have to transpose it.

Then $\varphi(a)$ have a simple meaning: $$\varphi(a) = (p_1,\ldots,p_s)^T(q_1,\ldots,q_s).$$ This is simply dot product!

This is also the integral of $\varphi$ over $a$, based on the idea that "integration is evaluation".

Stokes Theorem for smooth manifolds. Suppose

• $M$ is compact (smooth) oriented manifold ($\subset {\bf R}^N$),
• $\varphi$ is a (smooth) $(n-1)$-form.

Then $$\displaystyle\int_M d\varphi = \displaystyle\int_{\partial M}\varphi,$$ where the orientation of $\partial M$ is induced by that of $M$.

In this sense, $\varphi$ is an antiderivative of $d \varphi$.

Just in case, review...

• $n=0$, $N=1$, $M=[a,b]$, that's the Fundamental Theorem of Calculus.
• $n=1$, $N \geq 1$, then it's essentially the same

$$\displaystyle\int_C d\varphi^0 = \displaystyle\int_{\partial C} \varphi^0.$$ Here $C$ is a curve, $d \varphi^0$ is a $1$-form, $\partial C$ consists of $2$ points, and $\varphi^0$ is a $0$-form.

Corollary: If $\psi$ is exact, then $\displaystyle\int_M \psi = 0$, where $M$ is a manifold without boundary.

Proof: $$\displaystyle\int_M \psi = \displaystyle\int_M d\varphi = \displaystyle\int_{\partial M} \varphi = \displaystyle\int_{\emptyset} \varphi = 0$$ $\blacksquare$

What about exact forms with non-zero integral?

Example: In ${\bf R}^2$, $n=1$, $M=C$, closed curve.

So, $$\displaystyle\int_C \varphi^1 = 0?$$

No, not necessarily.

Question: Why does the hole (in $C$) matter?

Answer: The proof uses $\displaystyle\int_M \psi$. With a hole, $\partial M \neq C$.

So...

Topology matters

It matters in a very important way. In fact:

Calculus is topology.

The reasoning behind this principle is that the matrix of the exterior derivative $d$ is the transpose of the matrix of the boundary operator $\partial$ : $$d = \partial^T.$$

Recall that $\partial$ is defined on chains by way of cells. Given a $k$-cell $\tau$, $\partial \tau$ is made of ($k-1$)-cells.

The relation is also captured by this diagram:

$$ \newcommand{\lra}[1]{\!\!\!\!\!\!\!\xleftarrow{}\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{rlllllllllll} C^k(R) & \lra{iso} & C_k(R) \\ \ua{d} & & \da{\partial} \\ C^{k-1}(R) & \lra{iso} & C_{k-1}(R) \end{array} $$

So, if we know the boundary $\partial$ of each cell (topology) in terms of other cells, then you know all the derivatives (calculus) of all discrete functions and forms.

And this is how we extract topology from calculus: $$C^k(R)/_{\sim} = H^k(R),$$ for cubical cohomology. The left hand side is discrete calculus and the right hand side is the topology (in particular, Betti numbers).

So, this makes sense then:

calculus / algebra = topology.

Same idea for differentiable calculus: $$\Omega^k(R)/_{\sim} = H^k_{dR}(R)$$ and de Rham cohomology.

Discretization of calculus

Back to where we started...

Dimension 1. Given $f$ and $f'$, if you sample them: $g$ and $g^*$, we know that this pair don't satisfy the Fundamental Theorem of Calculus anymore.

Note: In numerical analysis, differences are used for derivatives.

.

The "derivative" is

• $f'(1)=f(1)-f(0)$,
• $f'(2)=f(2)-f(1)$,
• ...
• $f'(5)=f(5)-f(4)$.

Note: $\frac{f(2)-f(0)}{2}$, etc is used alternatively.

"Integrate" the derivative now, by summation. We end up with:

• $f(5)-f(0)$.

That's the integral over the interval! And FTC is satisfied too.

Problem: Where is $f'$ defined?

Above it's $1,..,5$. Or, we can redefine it as:

• $f'(0)=f(1)-f(0)$,
• $f'(1)=f(2)-f(1)$,
• ...
• $f'(4)=f(5)-f(4)$.

It's defined now on $0,...,4$.

In either case: domain $f \neq$ domain of $f'$!

In fact, FTC makes sense for

• $f(5)=\displaystyle\int_0^4 f'(x) dx$

but not for

• $\displaystyle\int_0^5 f'(x)dx$.

This suggests a favorable comparison of discrete exterior calculus over the "discretized" calculus.

Another example...

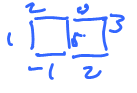
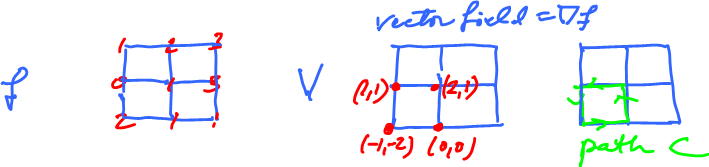
Dimension 2. Given a function $f$ on the grid, and its gradient, $V=\nabla f$, which is a vector field.

Compute: $$\displaystyle\int_C V ds = (-1,-2)(1,0) + (0,0)(0,1) + (2,1)(-1,0) + (1,1)(0,-1) = -4.$$

This is bad, because, being gradient, $V$ is a conservative vector field, so we should have $\displaystyle\int_C V ds = 0$!

Note: The good news is that $\displaystyle\int_C Vds \rightarrow 0$ as $\Delta x \rightarrow 0$, refining the grid. So the theorem is satisfied -- but only approximately.

Consider differential forms instead.

Now $f$ is a $0$-form, then $df$ is a $1$-form:

Therefore, $$\displaystyle\int_C df = -1 + 0 -1 + 2 = 0!$$

Again, the "discretized" calculus doesn't work as it should but discrete exterior calculus does.