Calculus and algebra vs topology

We revisit the subject of Topology via Calculus here but put it on a more solid, algebraic foundation.

Once again, we start with dimension $1$ and no forms.

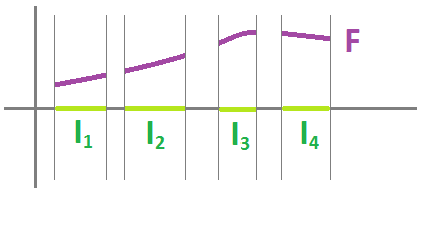
Suppose $R$ is the union of $m$ disjoint open intervals, $I_1,...,I_m$ in ${\bf R}$.

Question: What is the relation between the calculus over $R$ and the topology of $R$?

Both concepts are reduced to the minimum here. The calculus is reduced to differentiation and the topology of $R$ is reduced to the number $m$!

About the former, the whole story is in this linear operator: $$\frac{d}{dx}:C^1(R) \rightarrow C(R),$$ where the derivative operator takes continuously differentiable functions to continuous ones.

Let's find the topology (i.e., number $m$) in this operator.

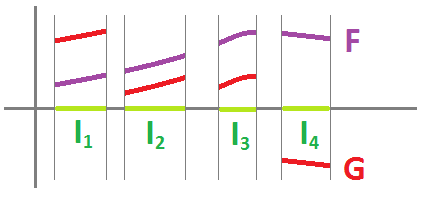
Suppose we are given a function $f \in C(R)$. Suppose also that $F \in C^1(R)$ is any antiderivative of $f$. Just like in calc 1, except this function is defined over a disconnected domain:

Now, how do we find the set of all antiderivatives of $f$? Each antiderivative $G$ differs from $F$ by a constant, on each interval:

Algebraically, each $G$ is defined piecewise, separately on each interval: $$G(x)=F(x)+C_k,x \in I_k,k=1,2,...,m.$$ Here $C_1,...,C_m$ are $m$ independent constants.

So, we have a correspondence:

antiderivatives parametrized by $m$ independent parameters $\leftrightarrow$ $m$ disjoint intervals.

We can interpret the former as: $$\left( \frac{d}{dx} \right) ^{-1}(f) = \{(F+C_1,...,F+C_m):C_k \in {\bf R} \} $$ $$\cong \{(C_1,...,C_m):C_k \in {\bf R} \}.$$ In other words, the derivative operator has $m$-dimensional preimages: $$\dim \left( \frac{d}{dx} \right) ^{-1}(f) = m.$$ Even though both of the vector spaces involved are infinite-dimensional!

In fact we know from linear algebra that the preimage of any point, which is an affine subspace, under a linear operator is its kernel, which is a linear subspace, "shifted": $$A^{-1}(v)=u+\ker A, u \in A^{-1}(v).$$ So, we can take this one step further: $$\dim \ker \left( \frac{d}{dx} \right) = m.$$ This statement has a simple interpretation, the kernel of the derivative operator consists of all constant functions, constant on each interval $I_1,...I_m$.

To summarize, the kernel of the derivative operator $$\frac{d}{dx}:C^1(R) \rightarrow C(R)$$ over a region with $m$ components has dimension $m$.

The latter is known as the 0th Betti number $b_0(R)$ of $R$.

Note: In ${\bf R}^n$, the question turns into, given a vector field, is it a conservative vector field (aka gradient vector field)? It's known to be related to the issue of independence of path, and we are back to topology.

Let's restate this for the exterior derivative instead.

We re-write $$\frac{d}{dx}:C^1(R) \rightarrow C(R),$$ as $$d:\Omega^0(R) \rightarrow \Omega^1(R).$$ The reasoning is as follows. First, functions are $0$-forms, so $$C^1(R) =\Omega^0(R),$$ as long as we limit our forms to $C^1$. Second, even though $1$-forms aren't functions on $R$, the vector spaces are isomorphic: $$C(R) \cong \Omega^1(R).$$ This isomorphism is given by: $$f \mapsto fdx.$$

So, the analysis above amounts to the following very compact formula:

Theorem. If the domain $R$ is the union of $m$ disjoint open intervals, then $$b_0=\dim \ker d_0.$$

It's not as simple if either

• the dimension of the domain $n>1$, or especially
• the degree of the forms $m>0$.