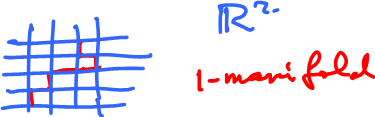This site is being phased out.
More about manifolds
Quotients of manifolds
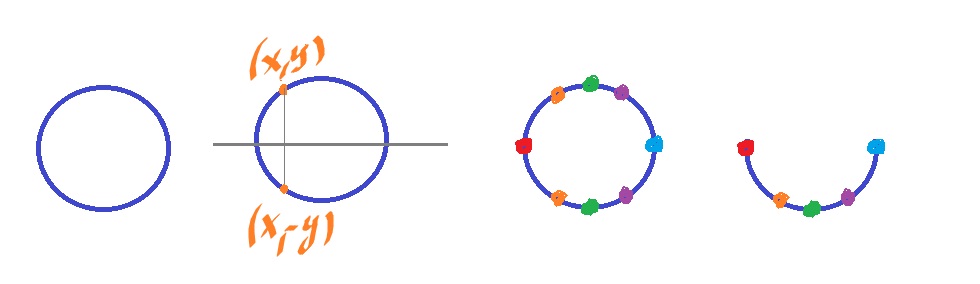
Example. Let consider the quotient of the circle ${\bf S}^1/_{\sim}$ with two different equivalence relations. The circle has neighborhoods of each point homeomorphic to ${\bf R}$, i.e., it's a $1$-dimensional manifold. Now we want to see the effect of gluing on its structure.
Suppose the circle is centered at $0$ on the $xy$-plane.
Firstly, suppose $$(x,y) \sim (x,-y).$$
In other words, each point is identified with the one symmetric with respect to the $x$-axis. Then $$X = {\bf S}^1/_{\sim} $$ is not a $1$-manifold because $(1,0)$ and $(-1,0)$ don't have neighborhoods homeomorphic to ${\bf R}$ anymore. Indeed, they are homeomorphic to the ray ${\bf R}^+$.
In fact, $X$ is simply the half circle: $${\bf S}^1/_{\sim} = {\bf I} = [0,1].$$
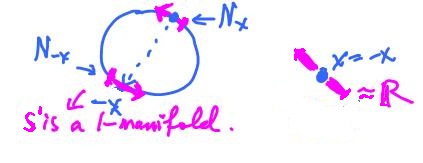
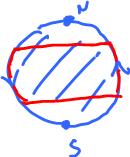
Example. Secondly, suppose $$(x,y) \sim (-x,-y). $$
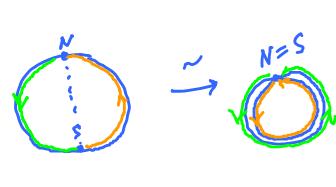
In other words, each point is identified with the one symmetric with respect the origin (the antipodal point). Then $X = {\bf S}^1/_{\sim}$ is still a $1$-manifold as the image shows.
What is it? It's another circle: $${\bf S}^1/_{\sim} = {\bf S}^1.$$
Exercise. Consider this kind of antipodal equivalence relation for the spheres ${\bf S}^2/_{\sim}$, ..., ${\bf S}^n/_{\sim}$ with $x \sim -x$.
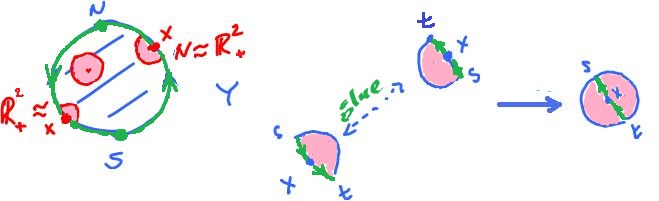
Example. Next, let's consider a certain quotient of the disk: $$Y = {\bf B}^2/_{\sim}.$$
First, observe that $${\partial}{\bf B}^2 = {\bf S}_1,$$ therefore the identification considered above applies:
In other words, the edge of the disk is glued to itself, with a twist.
Observe that even though the disk has a boundary, $Y$ is a surface without boundary. Indeed, a point $x$ on the edge has a neighborhood homeomorphic to half-disk but, when it's glued to its antipodal point, the two half-disks form a whole disk.
The end result is called the projective plane ${\bf P}^2$.
Why isn't it, say, the sphere? Because it contains the Mobius band:
Such surfaces are called one-sided, or non-orientable.
Manifolds on the grid
We have defined manifolds in a mathematical, indirect way. For applications, we would like to think about manifolds as certain kind of cubical complexes.
Specifically, how can we define manifolds on the grid?
Of course, we keep the definition, but we want to find an explicit definition of an $n$-manifold.
Recall that for each cell that belongs to the complex, so do all of its faces. What if this $n$-complex is an $n$-manifold?
Observe:
- There are no $k$-cells with $k>n$.
- The manifold is compact if and only if it has a finite number of cells.
- An ($n-1$)-cell is a face of one or two $n$-cells.
Since each $(n-1)$-cell on the grid belongs to exactly two $n$-cells...
item 3 above determines if this subset of the grid is an $n$-manifold without boundary:
- always two;
or with boundary:
- may be one.
Example:
This is a 1-manifold.
Example:
Problem, no patch $\simeq {\bf R}^2$ or ${\bf R}^2_+$.
Manifolds as preimages
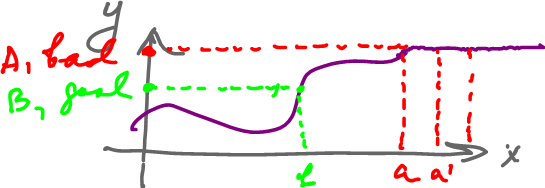
What we expect to see in dimension 2 is a relief:
It is the graph of a function $f \colon {\bf R}^2 \rightarrow {\bf R}$.
Suppose $f$ is continuous. Recall the notion of "level curves" from calculus (or more precisely we should be talking about level sets).
For a given $b \in {\bf R}$, it's the preimage of a point $$f^{-1}(b) = \{(x,y) \colon f(x,y)=b\}$$ under $f$.
Example: It's not always a curve.
If $f$ is constant, then $f^{-1}(c) = {\bf R}^2$ or $\emptyset$.
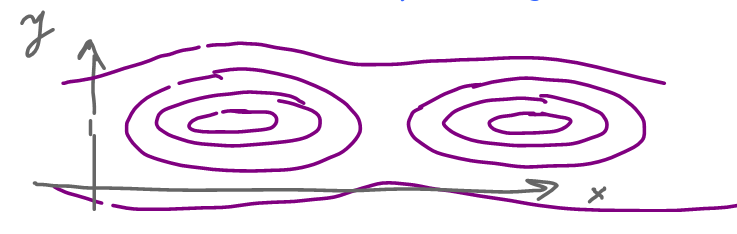
But "typically" we see this:
It does look like all of these are curves...
They are. But are they $1$-manifolds?
No, not all of them.
Not $1$-manifolds:
- out of range = empty,
- maximum/minimum = points,
- saddle points = crossed curves,
- locally constant = 2 dimensional.
Let's classify the level sets of a twice differentiable function.
Dimension 1: When is a level set of $f \colon {\bf R} \rightarrow {\bf R}$ a $0$-manifold?
Let's classify all $b$'s into two categories:
- the preimage $f^{-1}(b)$ contains only finitely many point(s), and
- the others.
The former is a $0$-manifold.
We know that this is the first option ahead of time if we compute the derivative at $x=a$ with $f(a)=b$ and $$f'(a) \neq 0.$$
Indeed, if $f'(a) > 0$, then $f'(x) > 0$ for $x \in (a-\delta,a+\delta)$, so $f$ is increasing on $(a-\delta,a+\delta)$. Then there is inverse $f^{-1}$ defined on some $(b-\epsilon, b+\epsilon)$ ("local inverse").
Hence $f^{-1}(b)$ is the preimage of $b$ under $f$ and $f^{-1}(b)$ is the value of $f^{-1}$ at $B$.
Simply put: $\{f^{-1}(b)\}$ is a single point, for the restriction of $f$.
Do same for each $b$, on a finite interval there will be only finite number of such $b$'s (follows from compactness). So yes, it's a $0$-manifold.
Dimension $2$: Given $f \colon {\bf R}^2 \rightarrow {\bf R}$, is $f^{-1}(A)$ a $1$-manifold?
Let's look for a pattern similar to the dimension $1$ case.
At maximum or minimum points, the partial derivatives equal zero, or, in coordinate free way: $${\rm grad} f(a)=0,$$ or even simpler $$f'(a)=0.$$ Same for a saddle though.
There are a few types of functions then...
For parametric curves: if $f \colon {\bf R} \rightarrow {\bf R}^N$, $A \in {\bf R}^N$, then $f^{-1}(A)$ is a $0$-manifold, if $f'(a) \neq 0$.
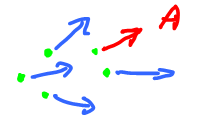
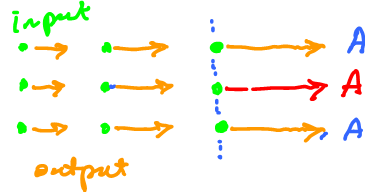
For vector fields: $f \colon {\bf R}^2 \rightarrow {\bf R}^2$ (input: points, output: vectors).
Is $f^{-1}(A) \subset {\bf R}^2$ a $0$-manifold? Turns out requiring $f'(a) \neq 0$ is not enough.
Example:
Clearly, $f'(a) \neq 0$ but $f^{-1}(A) \neq {\rm point}$!
Here $f^{-1}(A)$ is all these points, a whole line! Why? Because: there is no change of $F$ in this direction.
In terms of the derivatives we have here:
- $\frac{\partial f}{\partial x} \neq 0$, and
- $\frac{\partial f}{\partial y} = 0.$
To see why this is bad, consider the case when this does work.
Suppose $e_1, e_2$ basis in ${\bf R}^2$. When is $f'(e_1), f'(e_2)$ still a basis in ${\bf R}^2$?
Is it enough to require: neither is $0$?
No. It's possible that $f'(e_1)=f'(e_2)$! or $f'(e_1)=\lambda f'(e_2)$, etc...
Example:
In the "explosion", $f^{-1}(A) = {\rm point}$.
Now the solution...
Implicit function theorem. Given $f \colon {\bf R}^N \rightarrow {\bf R}^k$, $N \geq k$. Then $f'(a)$ is a linear operator, and we say that $a$ is a regular point (not singular) if $${\rm rank} f'(a) = k.$$ (recall $f_a' \colon {\bf R}^n \rightarrow {\bf R}^k$).
- Then $f^{-1}(A)$ is an $(N-k)$-manifold, where $A=f(a)$ (without boundary).
- Moreover, if $f \in C^k$ then $f^{-1}(A)$ is a $C^k$-manifold.
Explanation:
Given ${\bf R}^2 \rightarrow {\bf R}$, $N=2$, $k=1$.
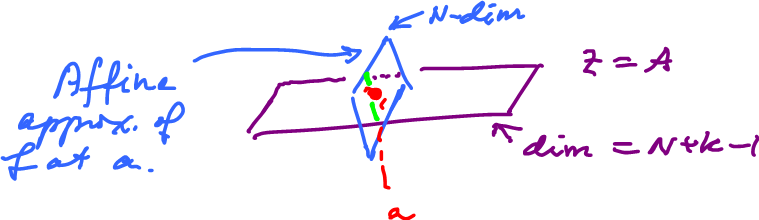
Then we are looking at the intersection of the graph of $f$ and the plane $z=A$, around the point $(a,A)$. Since $f$ is differentiable, it behaves as the tangent plane, essentially, at $a$. This plane is determined by $f'(a)$ and called also the best affine approximation.
So, it then suffices to consider the intersection of these planes...
In dimension $N+k$:
.
Condition ${\rm rank} f'(a)=2$ assures that the intersection of these planes is "transversal", so that it's a line. This line approximates the intersection of the graph with the plane. It turns out to be a $1$-manifold and so is its projection on the $xy$-plane.
Exercises
1. Consider these four sets:
- $A_r=\{(x.y):x^2-y^2=r\}$,
- $B_r=\{(x.y):x^2-y^2=r\}$,
- $C_r=\{(x.y):x^2-y^2=r\}$,
- $D_r=\{(x.y):x^2-y^2=r\}$,
parametrized by a real number $r$. For each answer: (a) Is it a surface? (b) If it is, what's its dimension? (c) Is it connected?
2. Suppose $f:R^n \rightarrow R^n$ is a smooth functions satisfying $ff=f$. (a) Prove that $f(R^n)$ is a smooth manifold. (b) What characteristic of $f$ determines the dimension of this manifold.
3. Describe the following manifolds:
- the set of straight lines through the origin in 3-space;
- the set of all great circles on the sphere;
- the set of number triples $(x:y:z)$ except $(0:0:0)$ modulo the equivalence relation $(x:y:z)\sim (kx:ky:kz)$ for all real $k$;
- the set of pairs $(p,q)$, where $q$ is a point on the plane and $p$ is a straight line through $q$;
- the configuration space of $n$ rigid bodies connected by rods consecutively with the ends fixed.