Projective plane

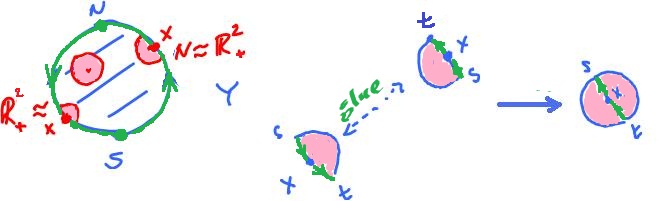
Let's consider a certain quotient of the disk: $$Y = {\bf B}^2/_{\sim}.$$

First, observe that $${\partial}{\bf B}^2 = {\bf S}^1.$$

On ${\bf S}^1$, consider this equivalence relation:

$u {\sim} -u$ for $u{\in}{\partial}{\bf B}^2.$

In other words, the edge of the disk is glued to itself, with a twist. The diagram of this operation is above.

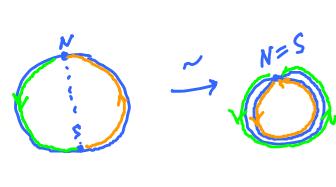
In ${\bf R}^2$, we have $$(x,y) {\sim} (-x,-y). $$ In other words, each point is identified with the one symmetric with respect the origin (the antipodal point).

What is it? It's another circle: $${\bf S}^1/_{\sim} = {\bf S}^1.$$

This result is called the projective plane, ${\bf P}^2$.

The projective plane is a surface without boundary. Indeed, a point $x$ on the edge has a neighborhood homeomorphic to half-disk but, when it's glued to its antipodal point, the two half-disks form a whole disk.

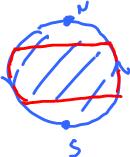
The projective plane is a non-orientable surface because it contains the Mobius band:

The $n$-dimensional projective space is

${\bf S}^n/_{\sim}$, where $u {\sim} -u.$

In particular, the $1$-dimensional projective space is the projective line. What is it?

${\bf S}^1/_{\sim}$, where $u {\sim} -u.$

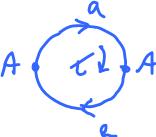
Let's compute the homology of the projective plane:

• $2$-cells: ${\tau}$ with ${\partial}$${\tau} = 2a$;
• $1$-cells: $a$ with ${\partial}a = 0$;
• $0$-cells: $A$ with ${\partial}A = 0$.

Then the real homology is $$H_1({\bf P}^2;{\bf R}) = {\rm \hspace{3pt} span \hspace{3pt}} \{ a \} / {\rm \hspace{3pt} span \hspace{3pt}}\{ 2a \} = {\bf R} / {\bf R} = 0,$$ but for the integral homology the same computation produces a very different result: $$H_1({\bf P}^2; {\bf Z}) = < a > / < 2a > = {\bf Z} / 2{\bf Z} ={\bf Z}_2,$$ generated by $[2a]$.

The other dimensions: $$H_2({\bf P}^2) = 0, H_0({\bf P}^2;{\bf Z}) = {\bf Z}.$$