This site is being phased out.
Relative topology
Contents
How a subset inherits its topology
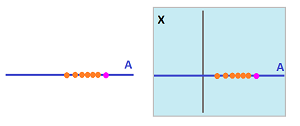
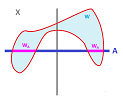
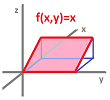
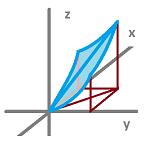
Is there a relation between the topology of the $xy$-plane and the topology of the $x$-axis?
The question may be that of convergence of sequences: if $x_n\to a$ then $(x_n,0) \to (a,0)$:
Or that of continuity of functions: if $f(\cdot,\cdot)$ is continuous, then $f(\cdot,0)$ is continuous too:
Or it may be about the interior, exterior, closure, etc.
There must be a relation!
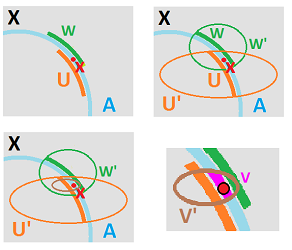
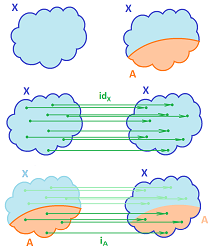
Example. Let's start with a simple example. Suppose $X$ is the $xy$-plane and $A$ is the $x$-axis. We know that the closeness (proximity) of points in $X$ is measured simply by the distance formula, the Euclidean metric. The distance between $(x,y)$ and $(a,b)$ is $$d\left((x,y),(a,b)\right):=\sqrt{(x-a)^2+(y-b)^2}.$$ But if these two points happen to lie on the $x$-axis ($y=b=0$), the formula turns into: $$d_A(x,a)=|x-a|,$$ which is the Euclidean metric of the $x$-axis. Not by coincidence, the proximity of points in $A$ is measured in a way that matches that for $X$.
$\square$
Thus, the case of metric spaces is clear: we take the metric $d$ of $X$ and apply it to the elements of $A$. The result is a metric for $A$.
Exercise. Prove that this construction does produce a metric.
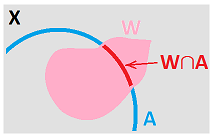
Next, we consider the respective topologies. Suppose we are given a point $a$ in $A$.
- If we treat $a$ as a point in $X$, then a neighborhood $W$ of $a$ in $X$ consists of points in $X$ within some $d>0$ from $a$.
- If we treat $a$ as a point in $A$, then a neighborhood $W_A$ of $a$ in $A$ consists of points in $A$ within some $d>0$ from $a$.
Of course, this is the same $d$. Then, $$W_A=W\cap A!$$
Example. In our example, the construction is easy to visualize:
- the Euclidean basis of $X:={\bf R}^2$ is the open disks;
- the Euclidean basis of $A:={\bf R}$ is the open intervals.
Now, intersections of disks with the $x$-axis produce intervals and, conversely, every interval in the $x$-axis is its intersection with a disk:
Of course, there are many different disks for each interval and some disks have no matching intervals.
$\square$
This idea applies to all topological spaces.
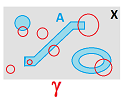
Following our original approach to topology via neighborhoods, a subset $A$ of a topological space $X$ with basis $\gamma$ will acquire its own collection $\gamma _A$ as the set of all of its intersections with the elements of $\gamma$:
In other words, $$\gamma_A := \{W \cap A :\ W \in \gamma_X \}.$$
Alternatively, we acquire the new topology $\tau _A$ for $A$ from the topology $\tau$ of $X$, in the exact same manner.
Theorem. The collection $\gamma_A$ so defined is a basis of neighborhoods in $A$.
Proof. If $x \in A \subset X$, then also $x \in X$. Since $\gamma_X$ is a basis on $X$, it satisfies (B1): there is some $W \in \gamma_X$ such that $x \in W$. Thus, we have $x \in A$ and $x \in W$, hence $x \in A \cap W \in \gamma_A$. Therefore, $\gamma_A$ satisfies (B1).
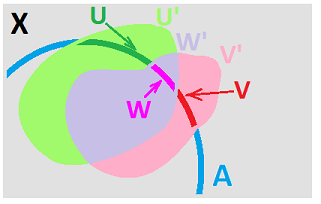
We need to prove (B2). Suppose we are given $U,W \in \gamma_A$ and a point $x \in U \cap W$. We need to prove that there is some $V \in \gamma_A$ such that $x \in V \subset U \cap W$.
By definition of $\gamma_A$, we have $$U = U' \cap A,\ W = W' \cap A \text{ for some } U',W' \in \gamma.$$
From (B2) for $\gamma_X$ we conclude:
Now let $$V:= V' \cap A.$$ Then, $x \in A$ and $x \in V$, hence $$x \in A \cap V = V' \in \gamma_A.$$ Also, $V' \subset U' \cap W'$ implies that $$V = V' \cap A' \subset U' \cap W' \cap A = (U' \cap A) \cap (W' \cap A) = U \cap W.$$ Therefore, $\gamma_A$ satisfies (B2).
$\blacksquare$
Definition. The topology generated by $\gamma_A$ is called the relative topology on $A$ generated by the basis $\gamma$ of $X$.
Let's review what happens to the neighborhoods in $X$ as we pass them over to $A$. Suppose $X$ is Euclidean with nice round neighborhoods:
Now the neighborhoods in $A$ are explicit and $X$ is gone:
In fact, since it doesn't matter how $A$ used to fit into $X$ anymore, we can even rearrange its pieces:
The topology of a subspace
What if the topology is given by a collection $\tau$ of open sets? Then how do we set up a topology for a subset?
In our example, all open sets in the $x$-axis $A$ can be seen as intersections of open sets in the $xy$-plane $X$:
Whether this is true in general is less obvious and will need a proof.
Generally, suppose we have a set $X$ and suppose $A$ is a subset of $X$. As we know, there are many ways to define a topology on $A$ -- if it is just another set. But suppose $X$ already has a topology, a collection of open sets $\tau$. Then,
All we need to do is to point out the sets we deem open within the subset. We choose, every time, $W_A = W \cap A$ for all $W$ open in $X$.
Suppose $\tau$ is the topology of $X$, then we define a collection of subsets of $A$: $$\tau_A := \{W \cap A : W \in \tau \}.$$
Theorem. $\tau_A$ is a topology on $A$.
Proof. Of course, the axioms of topology (T1) - (T3) for $\tau_A$ will follow from (T1) - (T3) for $\tau$.
For (T1):
- $\emptyset \in \tau \Rightarrow \emptyset = A \cap \emptyset \in \tau_A,$
- $X \in \tau \Rightarrow A = A \cap X \in \tau_A.$
For (T3):
- $U, V \in \tau_A \Rightarrow$
- $U = U' \cap A, V = V' \cap A$ for some $U', V' \in \tau \Rightarrow$
- $W=U \cap V = (U' \cap A) \cap (V' \cap A) = (U' \cap V') \cap A \in \tau_A,$
since
- $W'=U' \cap V' \in \tau.$
$\blacksquare$
Exercise. Prove (T2).
Definition. Given a topological space $(X,\tau)$ and a subset $A\subset X$, the topological space $(A,\tau_A)$ is called a subspace of $X$ and we say that its topology is the relative topology induced by $X$.
Compare this idea to that of a subspace of a vector space. In either case, the structure (topological or algebraic) is inherited by a subset. The main difference is that for vector spaces (or groups) the subset needs to be closed under the operations while for topological spaces a subset can always be seen as a subspace.
Note: In illustrations above, we attempt to choose a subset $A$ to be depicted as something “thin” in comparison to a “thick” $X$. The reason is that a thick $A$ might implicitly suggest that $A$ is an open subset of $X$ and that might make you rely on this subconscious assumption in your proofs.
Exercise. What is so special about the relation between $\tau$ and $\tau_A$ when $A$ is an open subset of $X$?
Once the topology on $A$ is established, all the topological concepts become available. We can speak of open and closed sets “in $A$” (as opposed to “in $X$”), the interior, exterior, closure, frontier, continuity, etc.
The following is obvious.
Theorem. The sets closed in $A$ are the intersections of the closed, in $X$, sets with $A$.
Exercise. If $A$ is closed in $X$ then sets closed in $A$ are...
Theorem. If $x_n\to a$ in $A\subset X$ then $x_n \to a$ in $X$.
Exercise. Prove the theorem.
The converse isn't true: while $x_n=1/n$ converges to $0$ in $X:={\bf R}$, it diverges in $A:=(0,1)$. This affects the limit points of subsets and, therefore, the closure.
Example. Here's a simple example that illustrates the difference between the closure in $X$ and the closure in $A \subset X$. Suppose
- $X := {\bf R},\ A := (0,1),\ B := (0,1),$
then
- in $X$, $\operatorname{Cl}(B) = [0,1]$,
- in $A$, $\operatorname{Cl}(B) = (0,1).$
$\square$
Exercise. Find a non-Euclidean topology (or a basis) on $X := {\bf R}^2$ that generates the Euclidean topology on $A$ the $x$-axis.
Exercise. Describe the relative topology of the following subsets of $X:={\bf R}$:
- $A:=\{1,2,...,n\}$,
- $A:={\bf Z}$,
- $A:=\{1,1/2,1/3,...\}$,
- $A:=\{1,1/2,1/3,...\}\cup \{0\}$,
- $A:={\bf Q}$.
Exercise. Show that if $B$ is a subspace of $A$ and $A$ is a subspace of $X$, then $B$ is a subspace of $X$.
Exercise. Suppose $A,B$ are disjoint subsets of a topological space $X$. Compare these three topologies:
- $A$ relative to $X$,
- $B$ relative to $X$, and
- $A\cup B$ relative to $X$.
It is a default assumption that any subset $A\subset X$ is a topological space with the relative topology acquired from $X$.
Relative neighborhoods vs. relative topology
An important, but easy to overlook, question remains, do $\gamma_A$ and $\tau_A$ match?
What do we mean by “match”? Starting with base $\gamma$ of $X$, we have acquired the topology $\tau_A$ of $A$ in two different ways:
- 1. taking all sets open with respect to $\gamma$ creates $\tau$ and then taking the latter's intersections with $A$ creates $\tau_A$; or
- 2. taking intersections with $A$ of $\gamma$ creates $\gamma_A$ and then taking all sets open with respect to the latter creates $\tau_A$.
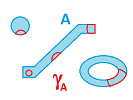
These two methods should produce the same result, as informally illustrated by the commutative diagram below: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} \gamma & \ra{open} & \tau \\ \da{\cap A} & & \da{\cap A} \\ \gamma_A & \ra{open} & \tau_A \end{array} $$
In particular, the above question needs to be answered, re-stated as follows: why are all the open sets in the $x$-axis the intersections of all the open sets in the $xy$-plane with the $x$-axis?
Theorem.
- $\tau_A$
- = the set of all intersections of the elements of $\tau$ with $A$
- = the set of all sets open with respect to $\gamma_A$.
Proof. To prove the equality we prove the mutual inclusions for these two sets.
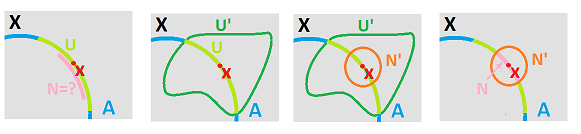
Part 1: $[\subset ]$ Given $U\in \tau_A$, show that $U$ is open with respect to $\gamma_A$. Suppose $x\in U$, we need to find $N\in \gamma_A$ such that $x\in N\subset U$. Of course, we construct $N$ as the intersection with a neighborhood of $x$ in $X$. Since $U$ is open in $A$, there is an open $U'$ in $X$ such that $U=U'\cap A$. Since $U'$ is open, there is a neighborhood $N\in \gamma$ such that $x\in N'\subset U'$. Now we take $N:=N'\cap A$.
Part 2: $[\supset ]$ It is less straight-forward and will require a subtle step. Suppose $U\in \tau_A$, i.e., it's open with respect to $\gamma_A$. We need to find $U'$ open in $X$ such that $U=U'\cap A$. Since $U$ is open in $A$, for every $x\in U$ there is $N_x\in\gamma_A$ such that $x\in N_x\in U$. Further, $N_x=N'_x\cap A$ for some $N'_x\in \gamma_X$. But, even though this set is open in $X$, it can't possibly give us the desired $U'$. The ingenious idea is to take all of these neighborhoods together: $$U':= \bigcup _{x\in U} N'_x.$$ It is open by (T2).
$\blacksquare$
Relative topology is the simplest way to create new topological spaces from old. The second simplest is the disjoint union.
Suppose two (unrelated to each other) topological spaces $X$ and $Y$ are given. One can form the disjoint union $Z:=X\sqcup Y$ of the underlying sets but what about the topology? What the definition of the topology of the disjoint union of these spaces ought to be? In other words, given topologies $\tau _X$ and $\tau _Y$, what should be the topology $\tau _Z$ on set $Z$? Out of the multitude of possibilities, we need to choose the one that makes most sense. What we want is for the topologies of $X$ and $Y$ to remain "intact" in $Z$. But just taking the union of $\tau _X \cup \tau _X$ would not produce a topology as (T1) fails!
In light of the above discussion, we want the relative topology of $X$ with respect to $Z$ to coincide with $\tau _X$ and same for $Y$. So, $$W\in \tau _Z \Leftrightarrow W\cap X\in \tau _X,\ W\cap Y\in \tau _Y.$$ The choice becomes clear: $$\tau _Z=\{U\cup V:\ U\in \tau _X,V\in \tau _Y\}.$$
Exercise. Prove that this is a topology. Also, what happens to the bases?
New maps
In light of this new concept of relative topology, we can restate a recent theorem.
Theorem. Suppose $f : X \to Y$ is continuous. If $X$ is path-connected the so is $f(X)$. In other words, the continuous image of a path-connected space is path-connected.
To follow the idea of piece-wise defined functions, two continuous functions can be “glued together” to create a new continuous function, as follows.
Theorem (Pasting Lemma). Let $A,B$ be two closed subsets of a topological space $X$ such that $X = A \cup B$, and let $Y$ also be a topological space. Suppose $f_A: A \to Y,\ f_B:B\to Y$ are continuous functions, and $$f_A(x)=f_B(x),\ \forall x\in A\cap B.$$ Then the function $f:X\to Y$ defined by $$f(x)= \begin{cases}{} f_A(x) & \text{ if } x\in A, \\ f_B(x) & \text{ if } x\in B, \end{cases} $$ is continuous.
Exercise. Prove the lemma. Hint: you'll have to use relative topology. State and prove the analog of the theorem with “closed” replaced by “open”.
Exercise. Show that the theorem fails if $A,B$ aren't closed. What if just one of them isn't?
Exercise. Prove that if $f:X\to Y$ is continuous then so is $f':X\to f(X)$ given by $f'(x)=f(x),\ \forall x \in X$.
Definition. For a one-to-one map $f:X\to Y$, its “partial inverse” $f^{-1}:f(X) \to X$ that is also continuous is called an embedding.
Exercise. Prove that an embedding $f:X\to Y$ creates a homeomorphism $f':X\to f(X)$.
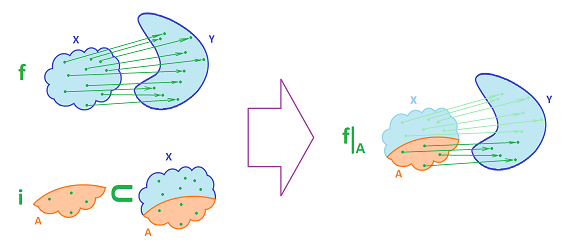
Definition. Suppose we have a topological space $X$ and a subset $A$ of $X$. Then the inclusion $i=i_A: A \to X$ of $f$ is given by $$i_A(x) := x,\ \forall x \in A.$$
For an open set $U$ in $X$, we have $$i_A^{-1}(U)=U\cap A,$$ so from the definition of relative topology, the result below follows:
Theorem. The inclusion function is continuous.
Notation. The notation often used for the inclusion is $$i=i_A:A \hookrightarrow X.$$
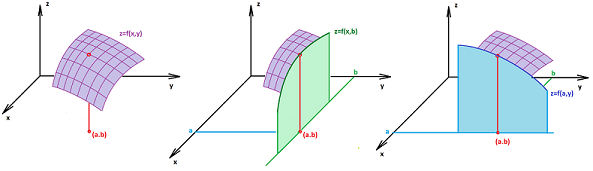
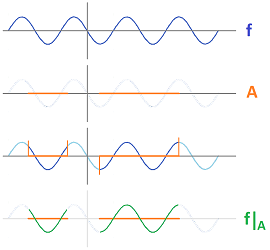
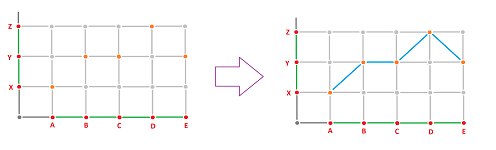
Next, notice that the picture below suggests that limiting the domain of a function will preserve its continuity:
Definition. Suppose we have topological spaces $X$ and $Y$, a map $f: X \to Y$, and a subset $A$ of $X$. Then the restriction $f\Big|_A: A \to Y$ of $f$ to $A$ is defined by $$f\Big|_A(x) := f(x),\ \forall x \in A.$$
In particular, we can understand inclusions as restrictions of the identity functions.
Theorem. Any restriction of a continuous function is continuous.
Proof. Suppose we have a continuous function $f : X \to Y$ and a subset $A$ of $X$. Suppose $U$ is open in $Y$. Then $$(f\Big|_A)^{-1}(U) = f^{-1}(U) \cap A.$$ As the intersection of an open, in $X$, set with $A$, this set is open in $A$. Hence, $f\Big|_A$ is continuous. $\blacksquare$
A less direct but more elegant proof is to observe that the restriction of a map to a subset is its composition with the inclusion of the subset: $$f\Big|_A=f i_A,$$ so that the diagram commutes: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} & A & \ra{i_A} & X \\ & _{f|_A} & \searrow & \da{f} \\ & & & Y \end{array} $$ Both are continuous and so is their composition.
Exercise. Suppose $i_A:A\to X$ is the inclusion. Suppose the set $A$ is given such a topology that for every topological space $Y$ and every function $f:Y\to A$,
Prove that this topology coincides with the relative topology of $A$ in $X$.
Let $X$ be a topological space and $A$ a subspace of $X$. A map $r:X \to A$ such that $r(x)=x$ for all $y \in A$ is called a retraction. We also say that $A$ is a retract of $X$. Another way of looking at this is that $$ri_A=\operatorname{Id}_A,$$ where $i_A$ is the inclusion of $A$ into X and $\operatorname{Id}_A$ is the identity map of $A$.
Exercise. Prove the following.
- Any point in a convex set is its retract.
- The $(n-1)$-sphere ${\bf S}^{n-1}$ is a retract of ${\bf R}^n \setminus \{0\}$ .
- The circle ${\bf S}^1$ is a retract of the Mobius band ${\bf M}^2$.
- The union of the equator and a meridian of the torus ${\bf T}^2$ is a retract of the torus with a point removed.
The extension problem
Just as we can restrict maps, we can try to “extend” them, continuously!
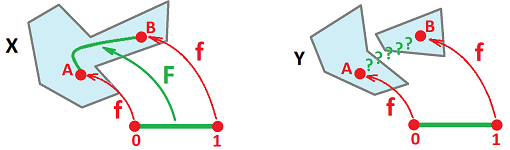
Definition. For $A\subset X$ and a given function $f:A\to Y$, a function $F:X\to Y$ is called an extension of $f$ if $F\Big|_A=f$.
The relation between the function and its extension can be visualized with a diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} & A & \ra{i_A} & X \\ & _{f} & \searrow & \da{F=?} \\ & & & Y \end{array} $$
Extension Problem. Is there a continuous $F$ to complete the diagram so that it is commutative?
Unlike the restriction problem above, the extension problem can't be solved by simply forming the composition. In fact, such an extension might simply not exist.
Of course, it is simple to extend a continuous function $f:[0,1]\to {\bf R}$ to $F:[0,2]\to {\bf R}$. But what about $f:(0,1)\to {\bf R}$ and $F:[0,1]\to {\bf R}$? For $f(x)=x^2$, yes; for $f(x)=1/x$ or $f(x)=\sin (1/x)$, no.
Exercise. State and prove the sufficient and necessary conditions for existence of an extension of $f:(a,b)\to {\bf R}$ to $F:(a,b]\to {\bf R}$.
A more interesting example comes from our recent study. We can recast the definition of path-connectedness of a topological space $X$ as the solvability of a certain extension problem: can every map defined on the end-points of the interval $$f:\{0,1\} \to X$$ be extended to a map on the whole interval $$F:[0,1] \to X?$$
Let's sneak a peek into how this approach will be used in algebraic topology. The first two diagrams below are:
- the extension diagram -- with topological spaces and maps, and
- its algebraic counterpart -- with groups and homomorphisms:
$$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccccccccc} &\{0,1\} & \ra{i_A} & [0,1] & & H_0(\{0,1\}) & \ra{} & H_0([0,1]) & & < 0,1 > & \ra{} & < 0 >\\ & & _{f}\searrow & \quad\quad \da{F=?} & & _{} & \searrow & \da{?} & & & \searrow & \da{?}\\ & & & X & & & & H_0(X) & & & & H_0(X) \end{array} $$ These groups are evaluated in the last diagram -- at least for graphs. But the way we construct the homology groups and homology maps make us realize that we can complete the first diagram only if we can complete the last one. But to do that -- for any given $f$ -- $H_0(X)$ would have to be $1$-dimensional!
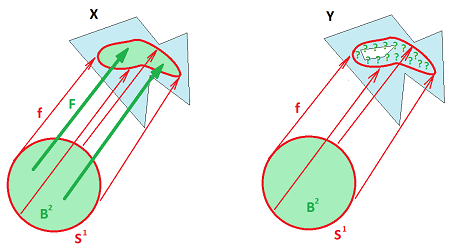
The worth of this approach becomes clearer as we start climbing dimensions. For example, we can also recast the condition related to simple connectedness as an extension problem: can every map of the circle $$f:{\bf S}^1 \to X$$ be extended to a map of the disk $$F:{\bf B}^2 \to X?$$
And so on for all dimensions, even those impossible to visualize...
Exercise. State and prove the sufficient and necessary condition for existence of a linear extension of a linear operator $f:A\to W$ to $F:V\to W$, where $V,W$ are vector spaces and $A$ is a subset of $V$.
Social choice: looking for compromise
The topic we will consider -- in several stages -- is social choice. By that we understand schemes that combine the choices several individuals have made into one.
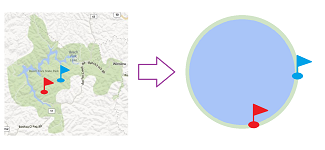
Let's imagine two hikers who are about to go into the woods and they need to decide where to set up their camp. Their preferred places don't match and we need to develop a procedure for them to find a fair compromise:
This procedure should be equally applicable to the future in case they decide to take a trip again.
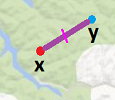
The answer is simple: take the middle point between the two locations, if possible:
Because of the last part, the answer depends on the geometry (and the topology!) of the set of possible choices, the forest.
So, this is what we have:
- the forest: a closed subset $W$ of ${\bf R}^2$,
- the location chosen by the first hiker: $x\in W$, and
- the location chosen by the second hiker: $y\in W$.
We need to find
- a compromise location $C\in W$,
and not just once, for these particular $x,y$, but for all possible $x,y \in W$. It is then a function, which we will call the choice function, $$f:W\times W\to W,$$ that we are after: $$f(x,y)=C.$$
Now, whenever $W$ allows, we choose the mid-point function: $$f(x,y):=\tfrac{1}{2}x+\tfrac{1}{2}y.$$ Such a choice is, of course, always possible when $W$ is convex. When it's not, the answer is unclear. So, we want to understand when this problem has a solution, a choice function $f$, depending on the set $W$.
But first, let's make sure that $f$ that we find will make sense as the answer in this particular situation.
First, the interests of both hikers should be taken into account equally. For example, a dictatorship won't be allowed: $$f(x,y)=x,\ \forall x,y.$$
We accomplish this by requiring that, if the two flip their preferences, the result will remain unchanged. Traditionally, this condition is called “anonymity”.
Anonymity Axiom (Symmetry). The choice function is symmetric: $$f(x,y)=f(y,x),\ \forall x\in W.$$
Exercise. Restate the axiom for the case of $m$ hikers.
However, a constant function $$f(x,y):=P,\ \forall x,y,$$ for some $P\in W$, demonstrates a kind of dictatorship (by a third party?) that passes the test of the Anonymity Axiom. This is why we also need to ensure that these two persons are the ones and the only ones who decide. We require that, if the two choices happen to coincide, that's the choice that will be made. Traditionally, this condition is called “unanimity”.
Unanimity Axiom (Diagonality). The choice function restricted to the diagonal is the identity: $$f(x,x)=x,\ \forall x\in W.$$
In other words, the diagonal of $W\times W$, $$\Delta (W):=\{(x,y)\in W\times W:\ x=y\} ,$$ is copied to $W$ by $f$.
Exercise. Restate the axiom for the case of $m$ hikers.
Of course, we will require $f$ to be continuous. The justification is the same as always: a small change in the input -- the choice of one of the two hikers -- should produce only a small change in the output -- the compromise choice. As another way to look at this, the error (because of limited accuracy) of the evaluation of the preferences won't dramatically change the result. Traditionally, this condition is called “stability”.
Stability Axiom (Continuity). The choice function $f:W\times W\to W$, where $W\times W \subset {\bf R}^4$, is continuous.
Exercise. Prove that the mid-point choice function, when it exists, satisfies the axioms.
Finally, the social choice problem is:
A positive answer won't tell us a lot. For example, if $W$ is homeomorphic to a convex set $Q$, we solve the problem for $Q$ and then bring the solution back to $W$:
Specifically, if $h:W\to Q$ is such a homeomorphism, our solution is: $$f(x,y)=h^{-1}\left( \tfrac{1}{2}h(x)+\tfrac{1}{2}h(y) \right).$$ The solution is fair as it doesn't favor one hiker over the other, but are they happy with it? Since all the geometry of $Q$ is lost in $W$, the “compromise” might be far away from either of the two choices.
Exercise. Prove that the nature of the problem is topological: if the problem has a solution for $W$, then it has a solution for every space homeomorphic to $W$.
We try to keep the conditions on $f$ as broad as possible and try to investigate what restrictions on the topology of $W$ will make it possible that $f$ does exist. The example of the mid-point solution above already suggests that $W$ might have to be acyclic.
Starting with the dimension $0$ features, does $W$ have to be path-connected?
Suppose not: $$W=W_1\sqcup W_2,$$ where $W_1,W_2$ are convex closed subsets of the plane. Suppose we pick a point $P \in W_1$ and define $$f(x,y)= \begin{cases} \tfrac{1}{2}x+\tfrac{1}{2}y & \text{ if } x,y\in W_1 \text{ or } x,y\in W_2, \\ P & \text{ otherwise. } \end{cases}$$ It is easy to see that the axioms are satisfied.
Exercise. Find a fairer choice function for the above situation.
The existence of the solution above indicates that, in a way, the axioms are too weak. In reality, the two persons may choose two different forests and there can't be a fair compromise. The unfairness is seen from the fact that, even though the two hikers are treated equally, the two forests aren't (as if someone made this pick ahead of time).
Exercise. Strengthen the Unanimity Axiom in such a way that we avoid this semi-dictatorship.
Next, does $W$ have to be simply-connected?
In practical terms, is it always possible to find a fair compromise between the two choices when there is a lake in the middle of the forest? To keep things simple, let's reduce the problem to the following:
- the hikers need to decide on a camping location on the shore of a circular lake:
When the two choices are close to each other, the solution can still be chosen to be the mid-point (along the arch). However, what if they choose two diametrically opposite points, $x=-y$? Then there are two mid-points. Which one do we choose for $f(x,-x)$? A possible solution is to choose the one, say, clock-wise from first to second but it violates the symmetry requirement.
Exercise. Show that it also violates the continuity requirement.
Exercise. What if, in the case of diametrically opposite choices $x,y$, we always select $f(x,y)$ to be the mid-point that lies in, say, the upper half of the circle?
We will demonstrate later that, even with these weak restrictions, there is no fair decision aggregation rule. Homology theory will be used as the tool to answer -- in the negative -- this and related social choice questions.
Discrete decompositions of space
The need to discretize the Euclidean space comes from our desire to study the world computationally. In order to understand what is the right way to discretize the space, we take, as an example, image processing.
An image is a grid of “pixels” marked in black and white (binary) or shades of gray (gray-scale):
Now, how do you capture objects depicted in the images? The idea is to break our continuous universe, the plane, into small, discrete (but still continuous!) elementary pieces and then use them to build what we want. For that to work, each of these pieces must be some kind of geometric object itself and not just a location. What are those elementary pieces?
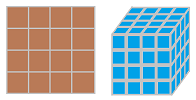
We start our decomposition by placing dots, or vertices, at the nodes of the grid:
To be able to form graphs, we also add the edges:
To form higher dimensional objects, we think of pixels as tiles and we think of voxels as bricks:
We want these building blocks, called cells, to be:
- 1. Euclidean,
- 2. topologically “trivial”, and
- 3. “small”.
First, even though the pieces are cut from the Euclidean space, we might end up with subsets with “exotic” topology.
Exercise. Show that the closure of the graph of $y=\sin (1/x)$ has three path-components but two of them aren't closed subsets.
To avoid these abnormalities, it makes sense to start, in the next subsection, with open subsets of ${\bf R}^n$. The advantage is that every point has a neighborhood homeomorphic to ${\bf R}^n$. These pieces are indeed Euclidean.
In the above example, vertices, edges, squares, and cubes are the cells. Since these pieces are discrete, we can model and study the universe with computers. On the other hand, we can put them all back together to reconstruct the space. And if we use only some of them, they will form objects with similar, Euclidean, properties.
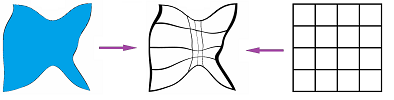
In general, the shapes of these pieces may be arbitrary. They may be squares, triangles, hexagons, etc., the shapes may vary within the same decomposition, and they may even be curved:
We also want these pieces to be topologically trivial: path-connected, no tunnels, no voids, etc. The idea is that the topological features of the objects formed by the cells come from the way they are put together not from the topology of each cell.
What makes these regular discretization schemes small is the possibility of refinement. Refining these decompositions into ones with smaller and smaller cells allows us to approximate the space -- with discrete structures -- better and better. Moreover, discrete functions defined on these discrete structures approximate continuous functions defined on the space:
Cells
Next, we formalize these ideas.
Definition.
- An open $n$-cell is a topological space homeomorphic to the Euclidean $n$-space ${\bf R}^n$.
- A closed $n$-cell, or simply an $n$-cell, is a topological space homeomorphic to the closed $n$-ball ${\bf B}^n$.
Initially, we look at cells as subsets of this Euclidean space ${\bf R}^n$. The simplest closed $n$-cell is then the closed $n$-ball located and the simplest open $n$-cell is its interior, the open $n$-ball.
As subsets, we can study their openness, closedness, interior, frontier, and closure. What they are for these simplest cells is quite obvious. However, if the ambient $n$-dimensional Euclidean space is fixed but the dimensions of the cells aren't, a cell of a lower dimension will have very different attributes.
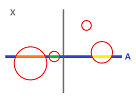
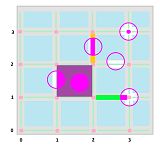
Example. In dimension $2$, we have for open cells: $$\begin{array}{l|l} 0 \text{-cell, vertex } P & \text{closed, not open} \\ 1 \text{-cell, edge } a & \text{neither open nor closed} \\ 2 \text{-cell, face } \sigma & \text{open, not closed} \end{array}$$ To see why, it suffices to look at how the Euclidean (disk) neighborhoods intersect these cells:
Also, $$\begin{array}{l} \operatorname{Int}(P) = \emptyset, \operatorname{Fr}(P) = P, \operatorname{Cl}(P) = P; \\ \operatorname{Int}(a) = \emptyset, \operatorname{Fr}(a) = a, \operatorname{Cl}(a) = a \cup \{ \text{the two end-points} \}; \\ \operatorname{Int}(\sigma) = \sigma; \\ \operatorname{Fr}(\sigma) = \displaystyle\cup \ 4 \text{ edges } \cup \ 4 \text{ vertices of the square} ; \\ \operatorname{Cl}(\sigma) = \text{the closed square}. \end{array}$$ $\square$
Next, we are to build new things with the cells by attaching them to each other along their “boundaries”. It is important to distinguish between:
- the frontier $\operatorname{Fr}(a)$ of a $k$-cell $a$ if it is treated as a subset of ${\bf R}^n,\ n \ge k$, and
- the boundary $\partial a$ of a $k$-cell $a$ if it is treated as a topological space of a special kind.
The former depends on $n$ while the latter doesn't, but it has to match the former under homeomorphisms when $k=n$. Then, what is the boundary?
Definition. A point $x$ in a $n$-cell $a$ is an interior point of $a$ if it has a neighborhood homeomorphic to ${\bf R}^n$; the rest are boundary points. The boundary $\partial a$ is the set of all boundary points of $a$.
This definition of the boundary is intrinsic!
Exercise. Show that each boundary point of an $n$-cell has a neighborhood homeomorphic to the half-space ${\bf R}^n_+$.
Exercise. Represent the boundary of an $n$-ball in ${\bf R}^n$ as the union of (a) closed $(n-1)$-cells, (b) open $(n-1)$-cells.
Exercise. Prove that the graph of $y=\sin\frac{1}{x},\ 0<x<1,$ can't be a part of the boundary of a $2$-cell in the plane.
Theorem. A homeomorphism of a $n$-cell $a$ to the $n$-ball $B$ in ${\bf R}^n$ maps the boundary points of $a$ to the points of the frontier of $B$. In other words, boundary goes to boundary.
Exercise. Prove the theorem. Hint: it's an embedding.