Chain complex

Sequences of chain groups

Suppose the ambient dimension $N$ is fixed as well as the integer grid ${\bf Z}^N$ of the Euclidean space ${\bf R}^N$. We introduce notation:

• $\mathcal{Q}$ is the set of all cells (of all dimensions) in the grid,
• $C_k(K)$ is the set of all $k$-chains in a given collection $K\subset \mathcal{Q}$ of cells, and, in particular,
• $C_k=C_k(\mathcal{Q})$ is the set of all $k$-chains in $\mathcal{Q}$.

We will $C_k(K)$ the $k$-chain group of $K$ and we call $C_k$ the total $k$-chain group.

Definition. Given a $k$-chain $s\in C_k$, $$s = a_1 + a_2 + ... + a_n,$$ where $a_1, a_2, ..., a_n$ are $k$-cells, the boundary $\partial s$ of $s$ is given by $$\partial s = \partial a_1 + \partial a_2 + ... + \partial a_n.$$

So, the boundaries of $k$-cells are $(k-1)$-chains, and, moreover, the boundaries of $k$-chains are $(k-1)$-chains as well. Thus, boundaries are found by a well-defined function $$\partial =\partial _k\colon C_{k} \to C_{k-1}.$$ It is called the boundary operator.

As before, we notice that this function is simply an extension of a function defined on the generators of a groups to the rest of the group -- by additivity. Therefore, we have

Theorem. The boundary operator is a homomorphism.

We now present the big picture of the algebra of chains and their boundaries.

The homomorphisms $\partial _k\colon C_{k} \to C_{k-1},k=1,2,...$, if written consecutively, form a sequence: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{cccccccccccccccccccc} C_{N} & \ra{\partial_N} & C_{N-1} & \ra{\partial_{N-1}} & ... & \ra{\partial_{k+2}} & C_{k+1} & \ra{\partial_{k+1}} & C_{k} & \ra{\partial_k} & ... & \ra{\partial_1} & C_{0}. \end{array}$$ As always, consecutive arrows are understood as compositions. Since we want all these groups treated uniformly, we append this sequence with two more items, one in the beginning and one at the end. Both are zero groups: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{cccccccccccccccccccc} 0&\ra{\partial_{N+1}}&...&... &... &... &\ra{\partial_0}&0. \end{array}$$ The two groups are attached to the rest of the sequence with homomorphisms that are, of course, zero. The result is this sequence of groups and homomorphisms called the ‘’chain complex’’ of $\mathcal{Q}$, or the total chain complex: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{cccccccccccccccccccc} 0&\ra{\partial_{N+1}}&C_{N}&\ra{\partial_N}&C_{N-1}&\ra{\partial_{N-1}}&...&\ra{\partial_{k+2}}&C_{k+1}&\ra{\partial_{k+1}}&C_{k}&\ra{\partial_k}&...& \ra{\partial_1}&C_{0}&\ra{\partial_0}&0. \end{array}$$

As we know, the chain groups $C_k(K),k=0,1,2,...$, can be defined for any set $K\subset \mathcal{Q}$ of cells. They are subgroups of $C_k=C_k(\mathcal{Q})$. Moreover, the chain complex comprised of these groups can be constructed as the one for the total chain groups -- if we can make sense of the boundary operators on these groups: $$\partial ^K _{k}:C_{k}(K)\to C_{k-1}(K),\forall k=1,2,3,....$$ Of course, these are the same cells and they have the same boundaries. That's why we define these homomorphisms as the restrictions of the boundary operators we have for the whole $\mathcal{Q}$: $$\partial ^K _{k} =\partial _k|_{C_{k}(K)}.$$ To make sure that these are well-defined, we need the boundaries of the chains in $C_k(K)$ to be chains in $C_{k-1}(K)$. This algebraic condition is ensured by a simple condition on the data of $K$ itself, below.

Definition. Suppose a set of cells $K\subset \mathcal{Q}$ satisfies:

• if $K$ contains a cell $a$, it also contains all of $a$'s faces.

Then $K$ is called a cubical complex.

The appearances of $K$ in the formulas will be routinely omitted and the chain complex of $K$ will look exactly as the one above for the total chain complex. It contains all topological information about the cubical complex.

Cycles and boundaries

Following the ideas that have arisen from our study of topology of graphs, we introduce the following definitions for a given cubical complex $K$ and each $k=0,1,...$.

Definition.

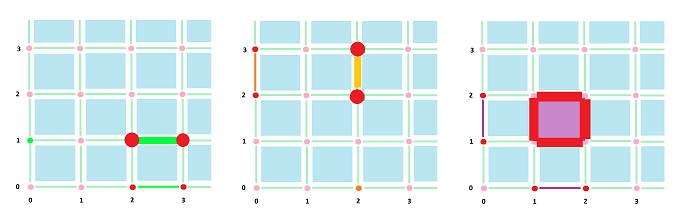
• A $k$-chain is called a $k$-cycle if its boundary is zero, and the $k$th cycle group is a subgroup of $C_k$ given by

$$Z_k=Z_k(K)=\ker \partial_k.$$

• A $k$-chain is called a $k$-boundary if it's the boundary of a $(k+1)$-chain, and the $k$th boundary group is a subgroup of $C_k$ given by

$$B_k=B_k(K)=\operatorname{Im} \partial_{k+1}.$$

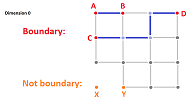
Let's review what form the analysis of graphs takes if we follow this algebraic insight. To do that we simply limit ourselves to the set $K$ of all $0$- and $1$-cells. This is how we visualize boundaries and cycles:

Now the chain complex is short: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{cccccccccccccccccccc} 0 & \ra{\partial_2} & C_{1} & \ra{\partial_1} & C_{0} & \ra{\partial_0} & 0. \end{array}$$ Of course, the diagram immediately leads to these two “triviality” conditions: $$\partial _2=0, \partial _0=0.$$

This is the reason why, for graphs, we only had to deal with a single boundary operator, i.e., $\partial _1$.

Another consequence of these two identities is these two familiar observations:

• every $0$-chain is a cycle, and
• the only $1$-boundary is $0$.

In other words,

• $Z_0=C_0$, and
• $B_1=0$.

The result would significantly simplify the analysis we are considering in the narrow case of graphs. In the general case, these two identities do reappear:

• $Z_0=C_0$, and
• $B_N=0$,

as a result of the triviality of the boundary operators at the ends of the sequence: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{rrrrrrrrrrr} 0& \ra{\partial_{N+1}=0} &C_N& \ra{\partial_{N}=?}& ... &\ra{\partial_{1}=?} & C_0 &\ra{\partial_{0}=0} &0 . \end{array} $$ The simplification this brings is limited to these dimensions.

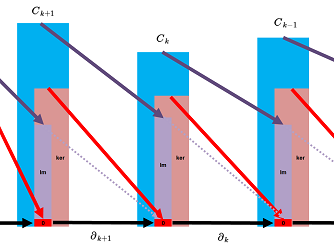
Further, both the cycle groups $Z_k$ as the kernels and the boundary groups $B_k$ as the images of the boundary operators can be connected to each other, as in this diagram: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{rrrrrrrrrrr} & \ra{\partial_{k+2}} & 0\in Z_{k+1}=\ker \partial _{k+1} & \ra{\partial_{k+1}} & 0\in Z_k =\ker \partial _{k} & \ra{\partial_{k}} & 0\in Z_{k-1}=\ker \partial _{k-1} & \ra{\partial_{k-1}} \\ & & \cap & & \cap & & \cap & & \\ & \ra{\partial_{k+2}}& \operatorname{Im} \partial _{k+2}=B_{k+1}\subset C_{k+1} & \ra{\partial_{k+1}} & \operatorname{Im} \partial _{k+1}=B_k \subset C_{k} & \ra{\partial_{k}} & \operatorname{Im} \partial _{k} =B_{k-1}\subset C_{k-1} & \ra{\partial_{k-1}} \end{array} $$ But these pairs of groups have even more intimate relation...

What is the relation between boundaries and cycles?

To answer this question let's try to answer another:

What is the boundary of a boundary?

Dimension $0$. The boundary of a vertex is zero, so the answer is zero.

Dimension $1$. The boundary of an edge is the sum of its two end-points and the boundaries of those are zero. So the answer is zero again.

Dimension $2$. The boundary of a square is the sum of its four edges. The boundary of each of those is the sum of its two end-points, or the vertices of the square. Each vertex appears twice and... the answer is zero again.

Example. To confirm this algebraically, compute the boundary of the boundary of a $2$-cell: $$\begin{array}{lllllll} \partial _1\partial _2 [n, n + 1] \times [m, m + 1] \\ = \partial _1( [n, n + 1] \times \{m \} + \{n \} \times [m, m + 1] + [n, n + 1] \times \{m + 1 \} + \{n + 1 \} \times [m, m + 1] ) \\ {\rm ... } \\ = 0. \end{array}$$

We can go on.

Dimension $3$. The boundary of a cube is the sum of its six square faces. The boundary of each of those is the sum of its four edges. Since these are the edges of the cube and each appears twice,... the answer is zero again.

Exercise. Prove the above algebraically.

So, it appears that, at least for the cells,

the boundary of a boundary is zero.

In other words, $$\partial _k\partial _{k+1} (x)=0$$ for any $(k+1)$-cell $x$.

Since the $(k+1)$-cells are the generators of the chain group $C_{k+1}$ and the values of the homomorphism $\partial _k\partial _{k+1}$ are zeroes, it follows that the whole homomorphism is trivial: $$\partial _k\partial _{k+1} \left(\sum_i s_{i}\right)=\sum_i \partial _k\partial _{k+1} (s_{i})=\sum_i 0=0.$$ The composition is trivial!

Theorem. The composition of two boundary operators $$\partial _{k}\partial _{k+1}:C_{k+1}\to C_{k-1}$$ is zero. Or simply put: $$\partial \partial = 0.$$

The conclusion holds for any cubical complex $K\subset \mathcal{Q}$.

Corollary. For any cubical complex $K$, $$\partial _{k}\partial _{k+1}=0:C_{k+1}(K)\to C_{k-1}(K),\forall k=1,2,3,....$$

Therefore, the answer to the question in the title is

every boundary is a cycle.

In other words, we have

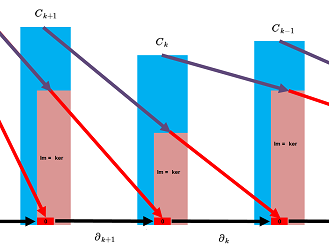
Corollary. For any cubical complex $K$, $$B_k(K)\subset Z_k(K),\forall k=0,1,2,...$$

That's what makes defining homology groups possible.

Definition. The $k$-th homology group, $k=0,1,2,3...$, of a cubical complex $K$ is given by $$H_k(K)=Z_k(K) / B_k(K).$$

The chain complex together with the kernels and the images of the boundary operators is given below: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccccccccccc} & \ra{\partial_{k+2}} & C_{k+1}& \ra{\partial_{k+1}} & C_{k}& \ra{\partial_{k}} & C_{k-1}& \ra{\partial_{k-1}} \\ & & \cup & & \cup & & \cup & & \cup \\ & \ra{\partial_{k+2}} & 0\in Z_{k+1}=\ker \partial _{k+1} & \ra{\partial_{k+1}} & 0\in Z_k =\ker \partial _{k} & \ra{\partial_{k}} & 0\in Z_{k-1}=\ker \partial _{k-1} & \ra{\partial_{k-1}} \\ & & \cup & & \cup & & \cup & & \\ & \ra{\partial_{k+2}}& \text{ im } \partial _{k+2}=B_{k+1}\subset C_{k+1} & \ra{\partial_{k+1}} & \text{ im } \partial _{k+1}=B_k \subset C_{k} & \ra{\partial_{k}} & \text{ im } \partial _{k} =B_{k-1}\subset C_{k-1} & \ra{\partial_{k-1}} \end{array} $$ This relation is frequently illustrated by this, informal, diagram:

When are cycles boundaries?

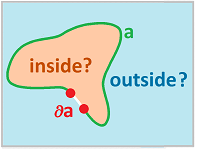
We have demonstrated that the boundary of every cycle is empty (i.e., zero). Indeed, a chain can't possibly enclose something inside if it has a boundary. Because at the boundary is where the inside would be connected to the outside and, therefore, there is no inside and outside!

So,

not cycle $\Rightarrow$ not boundary,

or

boundary $\Rightarrow$ cycle,

or $$B_k \subset Z_k.$$

Now, the other way around:

is every cycle a boundary?

Not if there is some kind of hole in the space! However, let's limit ourselves to the whole grid $\mathcal{Q}$ which has no topological features: components, tunnels, voids, etc., so it may be true.

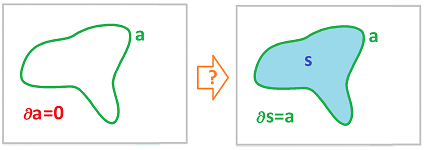
We start with $1$-cycles. The question we are asking is illustrated below:

And the picture suggests that the answer is Yes. Indeed, a rubber band on a table would surround a certain area (cf. Jordan theorem):

To make specific what the band bounds, we fill it with water to make it look like an above-the-ground pool:

But what if the rubber band is twisted?

In 3d, it is better to think of this problem as a soap film spanned on a, possibly curved, frame:

The answer still seems to be Yes, but try to stretch a film on a frame that isn't just twisted but knotted too:

As we shall see, the answer is “Yes, in a space of any dimension cycles are boundaries”. The conclusion applies equally to chains of all dimensions. For example, an air-balloon when closed (cycle!) will keep the air inside (boundary!).

Our conclusion affects the chain complex of the entire grid $\mathcal{Q}$ as follows: $$\text{im }\partial _{k+1} =\ker \partial _k,k>0.$$ Such a sequence is called exact. Indeed, the image isn't just a subset of but is equal to the kernel, exactly:

In general, the chain complex of a proper subset of the grid is inexact as the presence of topological features causes some cycles not to be boundaries. The degree of this inexactness is measured by means of homology.

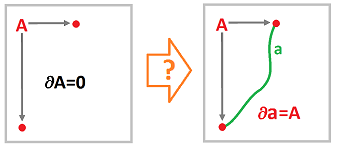
But what about the simplest case, chains of dimension $0$?

It's much simpler to visualize:

Mathematically, it's also simple. On the one hand, any one of the vertices on the grid is a cycle. On the other, every two vertices can be connected by a $1$-chain (just go vertical then horizontal). Therefore, any $0$-chain $a$ is the boundary of some $s\in C_1$ if $a$ has an even number of vertices present.

But what about chains with an odd number of vertices, such as a single vertex $0$-chain? It's not a boundary! The reason is that the boundary operator of any $1$-chain will always produce an even number of vertices, including $0$.

So, the answer to our question for $0$-cycles is “No, some of them aren't boundaries”. As it turns out, the $0$ dimension is an exception.

Exercise. Prove that that all non-boundaries are homologous to each other.