General Stokes Theorem

Let's look at the Fundamental Theorem of Calculus in the light of integration of differential forms.

Recall the statement: $$\displaystyle\int_a^b f(x) dx = F(b) - F(a),$$ where $F'=f$.

We want to restate it in ${\bf R}^1$ for forms...

The left-hand side is simply: $$\displaystyle\int_{[a,b]} dF.$$ It's the same for any parametrization of $[a,b]$, according to one of the properties.

What about the right-hand side?

Here $F(b) - F(a)$ is an integral, of $F$, over a $0$-manifold: $P=\{b\} \cup -\{a\}$.

Why not $\{a,b\}$?

Because the orientation of $P$ comes from ("is induced by") the orientation of $[a,b]$!

So, taken together the formula yields: $$\displaystyle\int_{[a,b]} dF = \displaystyle\int_{\{a,-b\}} F.$$

The version of this theorem for a $0$-form in ${\bf R}^n$ looks exactly the same: $$\displaystyle\int_C dF = F(b) - F(a) = \displaystyle\int_{\{a,-b\}} F,$$ but now $a,b$ are the endpoints of the curve $C$.

Observe here that if we think of $C$ as an oriented $1$-manifold, then its end-points constitute its boundary: $$\partial M = \{b\} \cup -\{a\}.$$

So, for the $n$-forms it generalizes to: $$\displaystyle\int_M dF = \displaystyle\int_{\partial M} F,$$ called the General Stokes Theorem. "General" here refers to the fact that it's about differential forms, of any degree: $F \in \Omega^1({\bf R})$, and, therefore, incorporates all integral theorems of vector calculus.

General Stokes Theorem for manifolds. Suppose

• $M$ is compact (piece-wise smooth) oriented manifold ($\subset {\bf R}^N$),
• $\varphi$ is a (piece-wise smooth) $(n-1)$-form.

Then $$\displaystyle\int_M d\varphi = \displaystyle\int_{\partial M}\varphi,$$ where the orientation of $\partial M$ is induced by that of $M$.

For dimension $1$ we still have this:

Theorem: If $F \in \Omega^1({\bf R}^n)$ and $M$ is a piecewise smooth $1$-manifold, then $\displaystyle\int_M dF = \displaystyle\int_{\partial M} F$.

Corollary: Suppose $\varphi \in \Omega^1({\bf R}^n)$ and $C$ is a curve. Then $\varphi$ is exact if and only if the integral $\displaystyle\int_C \varphi$ is independent of path.

Proof: ($\Rightarrow$) Stokes (or simply FTC).

($\Leftarrow$) If $\displaystyle\int_C \varphi$ is independent of path, then $F(x) = \displaystyle\int_C \varphi$ is well defined, where $C$ is any path from a given, fixed $A$ to $x$ (then $F(x)$ depends on $x$ only). Then $dF = \varphi$. $\blacksquare$

Example: Consider this form again: $$\varphi = -\frac{y}{x^2+y^2} dx + \frac{x}{x^2+y^2} dy$$ and prove it's closed.

Note: We didn't prove it's not exact, but let's just state what we know: $$\displaystyle\int_C \varphi = 2 \pi \neq 0,$$ where $C$ is the unit circle oriented counterclockwise.

Here $2 \pi$ means one turn. So $$\displaystyle\int_{-C} \varphi = -2 \pi,$$ $$ \displaystyle\int_{-C \hspace{3pt} {\rm twice}}\varphi = 4 \pi,$$ etc.

What about discrete forms? Is there an analogue of this result?

Yes. An analogue for $\varphi$ is cochain that's not exact.

Note: integration = summation (of the values of the form) and differentiation = difference.

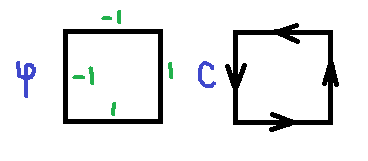
Example: Choose $\varphi ^1$ with orientation of the edges along the coordinate axes and a parametric curve $C$:

Since $$\displaystyle\int_C \varphi = 1+1+1+1=4,$$ we see that $\varphi$ is not exact.

But it is closed, since $d \varphi = 0$.

As it often happens in mathematics, good theorems are turned into definitions. We can use the Stokes formula to define the exterior derivative.

Given a $k$-form $\phi$, a $(k+1)$-form $\psi$ is called the exterior derivative of $\phi$ if for any chain $\omega$ $$\displaystyle\int_{\omega} \psi = \displaystyle\int_{\partial \omega} \phi.$$ The derivative is still denoted by $d \phi$.

In this spirit, the formula can be rewritten as $$d\phi(\omega)=\phi(\partial \omega),$$ or, in the common linear algebra notation, $$<d\phi,\omega>=<\phi,\partial \omega>.$$