Orientable surface

A surface is called non-orientable if it contains the Mobius band:

• Mobius band,
• Klein bottle,
• projective plane, etc.

The rest are orientable:

• sphere,
• cylinder,
• torus, etc.

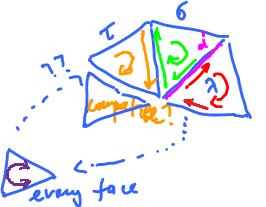
Definition. The orientations of two faces that share an edge are called compatible provided they induce the opposite orientations on the edge.

We can choose these orientations, if we deal with one edge at a time.

Can we ensure that all pairs of faces have compatible orientations?

We might proceed as follows. Start with $\sigma$ and $\tau$ compatibly oriented. Then, suppose ${\sigma}$ has another edge $d$ shared with face $\lambda$. Then $\lambda$ has to have the compatible orientation with ${\tau}$. Next, $\lambda$ has an edge $f$ shared with another face which has to have the compatible orientation with ${\tau}$, etc. At every step we move from a face to an adjacent face and every time the orientation of the next face is "forced". This may continue for a while. But what happens if we make a full circle and come back to ${\tau}$? It's possible that the orientation we want to impose on ${\tau}$ will be opposite of what we have already.

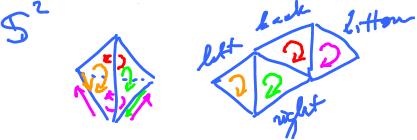
To sort this out, consider these two examples: triangulated sphere:

and Mobius band:

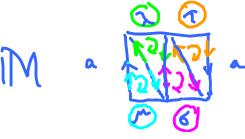
Is there a compatible orientation of the whole thing? Start with ${\tau}$, oriented clockwise. We orient ${\sigma}$ compatibly (generates opposite orientation on the edge they share) etc. For the Mobius band we have a problem:

• ${\tau}$ orients $a$ as $a$.
• ${\mu}$ orients $a$ as $a$.

They are not opposite! Therefore this is not a compatible orientation of ${\bf M}$.

Exercise. Show that there is no compatible orientation of the Mobius band, regardless of the triangulation.

Corollary. A non-orientate surface (contains ${\bf M}$) can't be compatibly oriented.

See also Orientable manifolds.

Theorem. Orientability is a topological invariant.