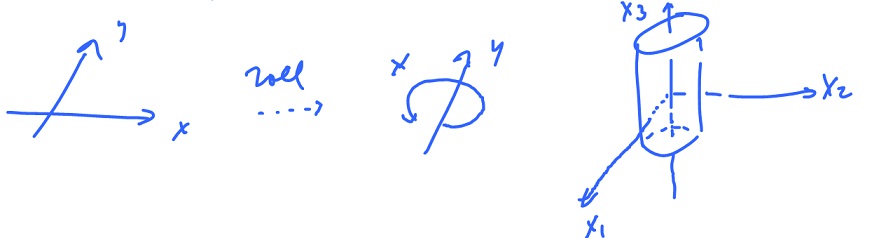Cylinder

As a quotient space

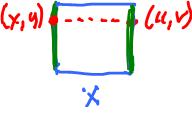
Represent the cylinder as a quotient space of a square.

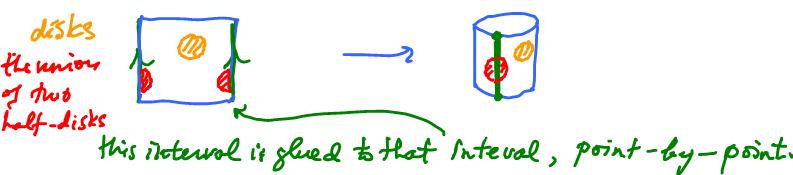
One can glue the two opposite edges of the square to create a cylinder. Here

$$X = [0,1] \times [0,1] = \{(x,y): x \in [0,1], y \in [0,1] \}.$$

And the equivalence relation is given by

$(x,y) \sim (u,v)$ if $y=v$ and $x,u=0$ or $1$, or simply $(0,y) \sim (1,y)$.

What happens to the topology? The preimage of an open disk under the quotient map is either a disk or the union of two half-disks at the edge.

The green arrows in the image above indicate how the two edges are attached to each other. If you reverse the orientation, you will get the Mobius band.

As a parametrized surface

Let's parametrize it. The idea is to take the plane (the input space) and roll it into the cylinder (the image).

Find $f: {\bf R}^2 \rightarrow {\bf R}^3$ such that the image of $f$ is the cylinder.

We want:

$y$-axis goes to $x_3$-axis.

To guarantee that we define $$f: \left| \begin{array}{} x_1 = f_1(x,y), x{\rm -axis \hspace{3pt} only} \\ x_2 = f_2(x,y), x{\rm -axis \hspace{3pt} only} \\ x_3 = f_3(x,y), {\rm \hspace{3pt} with \hspace{3pt}} f_3(x,y)=y. \end{array} \right|$$

So,

$( x, y )$ on $y$-axis is $( 0, y )$,

$$x_3 = f_3( x, y ) = f_3( 0, y ) = y.$$

($y = 0$, $x$-axis, it is rolled into a circle):

$x$-axis goes to the unit circle.

So we want to parametrize the circle $$f_1( x, y ) = \sin x$$

$f_2( x, y ) = \cos x$ (multi-layered),

$$f( x, y ) = ( \sin x, \cos x, y ).$$

Further rolling will create a torus.

As a product

The cylinder is the product of the circle and the interval. Hence its homology can be computed via the Kunneth theorem.