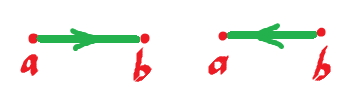Integration of differential forms of degree 0 and 1

Next, we consider integration of $0$-forms and $1$-forms -- on oriented manifolds of these dimensions.

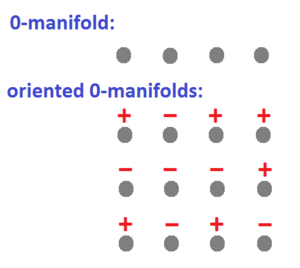
$0$-manifolds

Why does orientation matter in calculus?

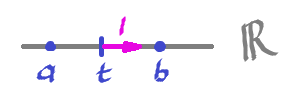
Recall from calc 1: $$\displaystyle\int_a^b f(x)dx = -\int_b^a f(x)dx.$$ If we rewrite this for oriented $1$-manifolds, we have: $[a,b]$ on the left and $[b,a]=-[a,b]$ on the right.

Simple enough... but we'll start with an even lower level, $0$-manifolds.

Now, $0$-manifolds are points, isolated points to be exact.

How do you "orient" those?

Well, manifolds with orientation (or "oriented manifolds") are manifolds with an extra structure (compare to a ring being a group with extra structure).

Specifically: for $0$-manifolds, every point is assigned a sign: $+$ or $-$, or a number $+1$ or $-1$.

Compare: a $0$-manifold and and oriented $0$-manifolds:

Note: Just like any manifold, a connected $0$-manifold (i.e., a single point) has exactly two possible orientations.

Definition: Given a $0$-form $\varphi$, the integral of the form $\varphi$ over oriented $0$-manifold $M=\{p\}$ is: $$\int_{\{p\}} \varphi = \left\{ \begin{array}{rl} \varphi(p) & \colon p {\rm \hspace{3pt} positively \hspace{3pt} oriented} \\ -\varphi(p) & \colon {\rm otherwise} \end{array} \right.$$

Why this way? The idea comes from the Fundamental Theorem of Calculus.

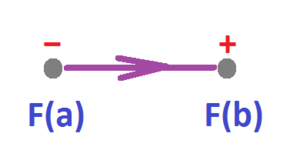
In the notation we have been using, it states that $$\displaystyle\int _{[a,b]} f(x)dx = F(b) - F(a).$$ But now we can also interpret the right hand side as an integral as well!

Indeed:

• $F(b) = \displaystyle\int_{\{b\}}F$, and
• $F(a) = \displaystyle\int_{\{a\}}F$.

So, the right hand side of the fundamental theorem of calculus is the integral of $F$ over a $0$-manifold of two points, $\{a,b\}$, with $a$ oriented positively and $b$ negatively. It's important to see that these orientations come from the orientation of the 1-manifold $[a,b]$, to be discussed later.

Definition: Once $\displaystyle\int_M \varphi$ is defined over points, $M = \{p\}$, we extend it over the finite unions, by additivity: if $$M = \{p_1, \ldots, p_s\},$$ then $$\displaystyle\int_M \varphi = \displaystyle\sum_{i=1}^s\int_{\{p_i\}}\varphi.$$

Definition: Given a $0$-manifold $M$, $-M$ is the same manifold with reversed orientation:

• $M = \{p_1, \ldots, p_s\}$ with signs $\epsilon_1, \ldots, \epsilon_s$ are each $+$ or $-$,
• $-M = \{p_1, \ldots, p_s\}$ with signs $-\epsilon_1, \ldots, -\epsilon_s$.

Theorem: $\displaystyle\int_{-M} \varphi = -\displaystyle\int_M \varphi$.

Proof: Easy. $\blacksquare$

What about the discrete case?

Recall:

• a discrete manifold = a combinatorial manifold = a manifold-like cubical complex.

Simple:

• $0$-manifolds $=$ vertices;
• $0$-form $=$ number assigned to each vertex.

Considering that integration is just summation, there is really no difference...

Orientations of $1$-manifolds

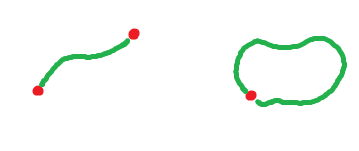
Let $M$ be a connected $1$-manifold with boundary.

It's a curve and there are only two options (why?):

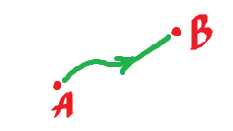
What is the meaning of the orientation of a smooth curve $C$?

Recall from calc 1, something we know about the Riemann integral:

Compare: $\displaystyle\int_a^b$ and $\displaystyle\int_b^a = -\displaystyle\int_a^b$.

This is where it comes from:

In this context, orientation is direction:

Here the curve goes from $A$ to $B$. It could also go from $B$ to $A$.

Simple enough...

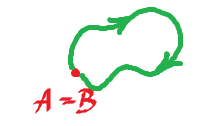
But what if $A=B$? Hmm...

Idea: use parametrization:

• $p \colon [a,b] \rightarrow C,$
• $p(a)=A$ and $p(b)=B.$

But this isn't enough to establish an equivalence relation between them to capture orientability...

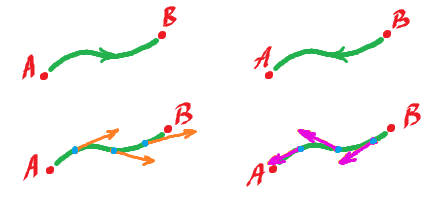
To formalize this idea, we can use tangents. Compare:

Question: But where do tangents come from?

Answer: the derivative $p'$.

Orange and green have the same orientation, purple opposite.

How do we tell that two parametrizations have the same orientation?

One idea: normalize them...

We can consider $\frac{p'(t)}{||p'(t)||}$ instead of $p'(t)$ for comparison. Then there is no confusion as long as we only use (differentiable) parametrizations with $p'(t) \neq 0$.

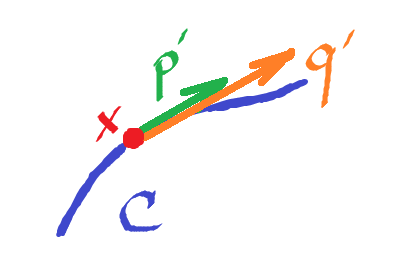
So, given two parametrizations $p$,$q$ of $C$:

• $p \colon [a,b] \rightarrow {\bf R}^N$, $p'(t) \neq 0$, $t \in [a,b]$ and
• $q \colon [c,d] \rightarrow {\bf R}^N$, $q'(s) \neq 0$, $s \in [c,d]$.

Here $p(t)=x$, $q(s)=x$, then we can assume $p'(t) = \alpha q'(s)$, for some $\alpha(x)$, for every $x$ on $C$. Then

• if $\alpha > 0$, then $p,q$ produce the same orientation; or
• if $\alpha < 0$, the orientations are opposite.

So, all parametrizations are split into two classes.

Are these, in fact, equivalence classes? Are there really exactly two of them? This requires proof. Exercise.

Integration of $1$-forms over oriented $1$-manifolds

Suppose $C$ is an oriented smooth $1$-manifold and $\varphi$ is a smooth $1$-form.

Let's define $\displaystyle\int_C \varphi$.

Suppose $C$ is parametrized by $p \colon [a,b] \rightarrow {\bf R}^2$.

Let's review line integrals (calc 3) first.

The line integral along $C$ (with respect to this parametrization), is, as an example, $$\displaystyle\int_C x dx + xydy = \displaystyle\int_a^b p_1(t)p_1'(t)dt + p_1(t)p_2(t)p_2'(t)dt.$$ Observe we use $p=(p_1,p_2)$ and then substitute $x = p_1(t)$ and $y=p_2(t)$.

We want this integral (which could be the work for example) to be independent of parametrization (but dependent on orientation).

We use the definition of $1$-form as a function $$\varphi \colon {\bf R}^n \times T{\bf R}^n \rightarrow {\bf R},$$ i.e., a location, a vector at the location $\mapsto$ a number.

Definition. The integral of a $1$-form over a oriented $1$-manifold $C$ parametrized by $p \colon [a,b] \rightarrow {\bf R}^n$ is $$\displaystyle\int_C \varphi = \displaystyle\int_a^b \varphi(p(t),p'(t))dt.$$

The composition $\varphi(p(t),p'(t))$ indeed makes sense since $$(p(t),p'(t)) \in C \times TC \subset {\bf R}^n \times T{\bf R}^n.$$

The integral of type $\displaystyle\int_a^b f(x)dx$ is familiar from calc 1. Let's translate it into the new language.

What are $C$, $p$, $\varphi$ for this integral?

• $C=[a,b]$,
• $p(t)=t$,
• $\varphi = f(x) dx$.

Then

$\begin{align*} \displaystyle\int_c \varphi &= \displaystyle\int_a^b \varphi(p,p')dt \\ &= \displaystyle\int_a^b \varphi(t,1)dt \end{align*}$.

Note: Here, $\{1\}$ is the basis of $T{\bf R}$

Substitute:

$\begin{align*} \varphi(t,1) &= (f(x) dx)(t,1) \\ &= f(t)(dx)(1) (dx {\rm \hspace{3pt} evaluated \hspace{3pt} at \hspace{3pt}} 1)\\ &= f(t) \cdot 1 \\ &= f(t), \end{align*}$

so $$\displaystyle\int_c \varphi = \displaystyle\int_a^b f(t)dt,$$ as expected.

Recall also that this is the area under the graph of $f$. Therefore, it is independent of parametrization, as requested!

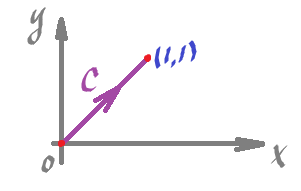
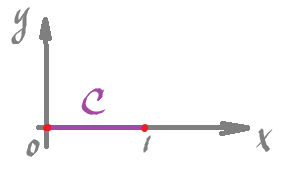
Example: In dimension $2$, consider, as an example, $C$ is this segment:

and $$\varphi = x dx + dy.$$

Parametrize the curve,

• $p \colon [0,1] \rightarrow {\bf R}^2$,
• $p(t) = (t,t)$.

Then $$\begin{align*} \varphi(p,p') &= (xdx + dy)((t,t),(1,1)) \\ &= t \cdot (dx)(1,1) + (dy)(1,1) \\ &= t((dx)(1,0) + (dx)(0,1)) + ((dy)(1,0)+(dy)(0,1)) \\ &= t+1 \end{align*}$$

Therefore, $$\displaystyle\int_C \varphi = \displaystyle\int_0^1 (t+1) dt = \left. \frac{t^2}{2}+t\right| _0^1 = \frac{3}{2}.$$

Exercise: Consider

• $\displaystyle\int_C \varphi$, where
• $C = $ upper half circle, and
• $\varphi = ydx + xdy$.

What if $C$ is not smooth? It won't work if $p'$ is undefined.

What if $C$ is piecewise smooth?

Definition: Suppose the curve is the union of finitely many smooth curves, $$C = C_1 \cup \ldots \cup C_s,$$ each of which is smooth. Then define $$\displaystyle\int_C \varphi = \displaystyle\sum_{i=1}^s\int_{C_i} \varphi.$$ (Think of this as the additivity of the integral.)

Why do we care about this issue?

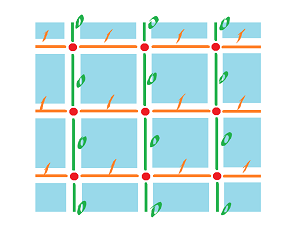
Discrete forms are defined on the grid!

Indeed, a discrete curve is made of vertical and horizontal pieces. So it's not smooth, but it is piecewise smooth.

Then, it suffices to define $\displaystyle\int_C \varphi$ for $C$ being vertical edge or horizontal edge (and then use additivity).

Consider horizontal,

parametrize $p \colon [0,1] \rightarrow {\bf R}^2$ by $p(t) = (t,0)$.

Then, $$\begin{align*} \int_C \varphi &= \int_0^1 \varphi(p,p') dt \\ &= \int_0^1 \varphi((t,0),(1,0)) dt \\ &= \int_0^1 m dt \\ &= m, \end{align*}$$

where $m$ is the value of $\varphi$ on $C$. Same for vertical edges.

Note: What if the length of the grid cell is $h$? Then $\displaystyle\int_C \varphi = mh$.

So, $$\displaystyle\int_C \varphi = \displaystyle\sum_{i=1}^s m_i,$$ if $C = $ union of edges $e_1, \ldots, e_s$ with $\varphi(e_i)=m_i$.

Integration is just summation (watch out for orientation though).

Discrete forms

Integration allows us to formalize the relation between smooth forms and discrete forms (as cochains).

For example, $dx$ continuous vs. $dx$ discrete.

What about the definition of a continuous form as $\varphi \colon {\bf R}^2 \times {\bf R}^2 \rightarrow {\bf R}$ and its multi-linearity? What does it have to do with cochains?

Recall, $1$-cochain is $\varphi \colon 1$-cells $\rightarrow {\bf R}$, just any function.

But, $1$-cells can be combined into $1$-chains $=$ formal linear combinations of cells: $$\displaystyle\sum_{i=1}^n \alpha_i c_i,$$ where $\alpha_i \in {\bf R}$, $c_i$ are $1$-cells. They form $C_1({\bf R}^2)$, a vector space (assuming ${\bf R}^2$ has the grid).

Then $\varphi$ can be extended to $$\varphi \colon C_1({\bf R}^2) \rightarrow {\bf R}$$ by linearity: $$\varphi\left(\displaystyle\sum_{i=1}^n \alpha_i c_i\right) = \displaystyle\sum_{i=1}^n \alpha_i \varphi(c_i).$$

That's the meaning of "co" in "cochain". It's a linear function to ${\bf R}$ on chains (see Dual spaces).

Let's construct a cochain from a given continuous differential form, $\omega \in \Omega^1({\bf R}^2)$. It's very simple.

Suppose ${\bf R}^2$ has a grid.

Definition. The cochain corresponding to a given continuous form $\varphi$ is defined as $$\varphi(a) = \displaystyle\int_a \omega,$$ where $a$ is a $k$-cell.

From this point of view,

integration = evaluation.

This is a canonical way of discretizing calculus over any grid or mesh.

In particular, all standard operators of vector calculus:

• ${\rm grad}$,
• ${\rm curl}$,
• ${\rm div}$,

are automatically discretized as $d$, the exterior derivative, in appropriate dimensions.

Note: This is also a way of modeling with PDEs.

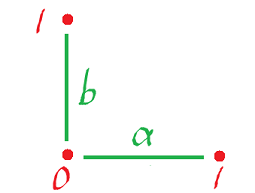
Example: Let $\omega = dx$, find the corresponding $\varphi \in C^1({\bf R}^2)$.

Let $\varphi \colon 1$-cells $\rightarrow {\bf R}$. Pick a cell:

(horizontal and vertical). Then $$\varphi(a)=\displaystyle\int_a \omega = \displaystyle\int_0^1 \omega(p,p') dt,$$ where $p \colon [0,1] \rightarrow a$ is a parametrization of $a$.

Then $p(t)=(t,0)$, substitute (same as $dx(i)$): $$\begin{align*} \varphi(a) &= \int_0^1 dx((t,0),(1,0)) dt \\ &= \int_0^1 1 dt \\ &= 1. \end{align*}$$

Next, $p(t)=(0,t)$, substitute (same as $dx(j)$): $$\begin{align*} \varphi(b) &= \int_0^1 dx((0,t),(0,1)) dt \\ &= \int_0^1 0 dt \\ &= 0. \end{align*}$$

Same for all other vertical and horizontal $1$-cells. Then $\varphi$ is:

All horizontal edges are assigned $1s$ and vertical $0s$.

It's the opposite for $dy$. This matches our prior definitions.

Question: What about vice versa? How do you get a continuous form from a cochain?

Answer: Interpolation, to be discussed later.