This site is being phased out.
Calculus I -- Spring 2017
MTH 229 - Calculus with Analytic Geometry I (CT). An introduction to analytic geometry. Limits, derivatives, and integrals of the elementary functions of one variable, including the transcendental functions. (PR: MTH ACT of 27 or above, or MTH 130 and 122, or MTH 127 and 122, or MTH 132) This course meets a Core I/Critical Thinking requirement.
- Time and Place: 5:00 pm - 5:50 pm MW and 5:00 pm - 6:15 pm TR at 518 Smith Hall.
- Instructor: Peter Saveliev (call me Peter)
- Office: Smith Hall 713
- Office Hours: MW 2:30 - 5:00, or by appointment
- Office Phone: x4639
- E-mail: saveliev@marshall.edu
- Class Web-Page: math01.com
- Prerequisites: fluency with algebra, good understanding of functions
- Text: Calculus by Rogawski and Adams, Chapters 2 - 5
- Goals: good understanding of limits, the derivative and the integral, fluent differentiation
- Computer Restrictions: graphic calculator TI-83 or TI-83+
- Activities: the student will practice each outcome via the homework given in the textbook and online.
- Evaluation: the student achievement of each outcome will be assessed via
- in-class quizzes: taken from the textbook's exercise sets
- homework: accessed and graded online, provided by Webwork, http://webwork.marshall.edu/webwork2/S17-Math-229-Saveliev/
- in-class tests: based on the textbook's exercises
- project(s): written applications of calculus in real life
- Grade Breakdown: TOTAL $= .05 \times P + .25\times (Q + H) + .20\times FP + .20\times M + .30\times F$
- participation: $5\%$
- quizzes and online homework: $25\%$
- final project: $20\%$
- midterm: $20\%$
- final exam: $30\% $
For other details, see Course policy.
Contents
Lectures
They will appear here as the course progresses.
- Set 1
- Set 2
- The derivative
- Set 3
- Differentiation
- Set 4
- Differentiable calculus
- Set 5
- Applications of differential calculus
- The integral
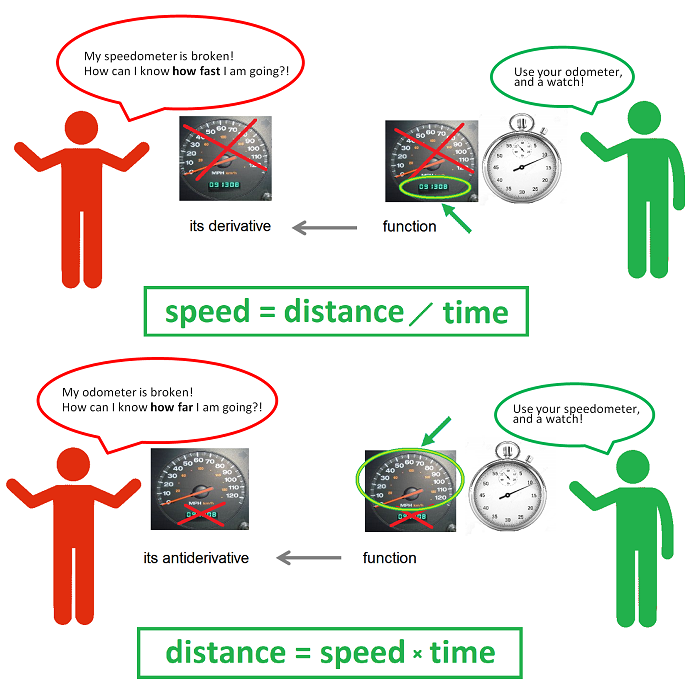
Calculus in one picture...
Projects
The student will be given a short, one or two sentences, description of a problem that uses no calculus terminology.
- Stage 1: The student's first task is to ask the right questions in order to recast the problem in the language of the appropriate mathematics. It also includes critique of the old submission.
- Stage 2: Then he is to explore the problem numerically and graphically with a spreadsheet and make an approximation of what the answer might be and ask further questions.
- Stage 3: Finally, the problem is solved analytically with the calculus tools and the answer is confirmed.
All the steps, the explanations of the methods, the data, the illustrations, and the computations are presented in writing. The methods should be based entirely on the material of the course.
The actual project statements are written as if by a person with no knowledge of calculus. That is why the problems may be poorly formulated, incomplete, and have many possible answers or none at all. As a result, the structure of the project might be much more complex than the three stages above.
Project statements:
- 1. How do I throw a ball down a staircase so that it bounces off each step? -- (fall 2016)
- 2. How should you throw a ball from the top of a $100$ story building so that it hits the ground at $100$ feet per second? -- (spring 2017, fall 2016)
- 3. I would like to use a cannon with a muzzle velocity of $100$ feet per second to bombard the inside of a fortification $300$ feet away with walls $20$ feet high. -- (spring 2017, fall 2016)
- 4. I have a toy cannon and I want to shoot it from a table and hit a spot on the floor $10$ feet away from the table. -- (spring 2017, fall 2016)
- 5. How hard do I have to push a toy truck from the floor up a $30$ degree incline to make it reach the top of the table at zero speed? -- (spring 2017, fall 2016)
- 6. How much does moving in or out of the passing lane affect the reading of a radar gun? -- (spring 2017, fall 2016)
- 7. How fast does the shadow of a falling ball on a sliding ladder move? -- (spring 2017)
- 8. How fast do I have to move my hand while spinning a sling in order to throw the rock $100$ feet away? -- (spring 2017, fall 2016)
- 9. Where should I stand in order to be best illuminated by two light bulbs on the ceiling if the amount of light is inversely proportional to the square of the distance? -- (spring 2017)
Instructions:
- A group should contain one or two persons.
- Your submission should be both on paper and in a digital format such as PDF (it will be linked here).
- It is a good idea to go digital from the beginning; for example, write with Latex or MS Word, draw with MS Paint, analyze data with MS Excel or Google spreadsheets.
- Include: the name, the title, introduction, conclusions, labeled pictures and tables, references, etc.
- The Excel file with the “free fall” equations is here for download, some explanations are here.
- Due date: April 23
Description
List of topics
- Brief review of basic concepts of algebra
- Number systems. Distance formula. Slope of a line. Standard equations of lines.
- A library of functions
- The basic equations and qualitative behavior of linear functions, power functions, polynomial functions, rational functions, exponential and logarithmic functions, and trigonometric functions.
- Limits and applications
- The limit of a function at a point. One-sided limits. Continuity and the intermediate value theorem. Infinite limits. Limits at infinity. Applications of limits to engineering and science.
- Differentiation and applications
- Definition of the derivative at a point and on an interval. Slope of a tangent line. Derivatives of polynomials. Derivatives of trigonometric functions. Derivatives of exponential and logarithmic functions. Rules for differentiation. Mean value theorem. Implicit differentiation. Maxima and minima. Critical points and intervals of increase and decrease. Concavity and inflection points. Newton's Method. Differentials and linear approximation. Applications of derivatives to engineering and science.
- Integration and applications
- Area as an integral. Antiderivatives. Riemann sums. Definite integrals as limits of Riemann sums. The Fundamental Theorem of Calculus. The substitution method for integrals. Applications of integrals to engineering and science.
Learner outcomes
- 1. Students will be able to evaluate limits, derivatives, and integrals symbolically.
- 2. Students will be able to approximate limits, derivatives, and definite integrals from tabular and graphical data.
- 3. Students will be familiar with the definitions of limits, derivatives, and integrals; be able to apply these definitions to test properties of these concepts; and be able to produce verbal arguments and examples showing that basic properties hold or do not hold.
- 4. Students will be able to apply the techniques of calculus to answer questions about the analytic geometry of functions, including vertical and horizontal asymptotes, tangent lines, local extrema, and global extrema.
- 5. Students will be able to verbally explain the meaning of limits, derivatives, and integrals in their own words, both in general terms and in the context of specific problems.
- 6. Students will be able to select or construct an appropriate function to model an applied situation for which calculus is applicable, based on a verbal description of the situation.
- 7. Students will be able to apply techniques of calculus to solve applied problems from fields such as engineering and the sciences.
- 8. Students will be able to interpret symbolic and numerical results in real-world terms, and analyze the validity of their results in a real-world setting.
Course goals
- To give students an understanding of the fundamental concepts of calculus and an appreciation of its many applications.
- To develop critical thinking skills by asking students to convert real-world problems into forms suitable for calculus, and interpret the results of calculus in real-world terms.
- To provide students with a deeper understanding of the mathematics that is used in their science and engineering courses.
- To develop facility in using graphing calculators and computers to solve mathematics problems.
- To satisfy program requirements.
Tutoring
The math tutoring lab will be open this semester during the following hours:
- Smith Music 115: Monday-Thursday 10am-4pm, Friday 10am-12noon;
- Smith Hall 620: Monday-Thursday 5:00pm-6:30pm.
The lab will open the second week of classes.
More information: http://www.marshall.edu/math/tutoringlab.asp.
Also, the university tutoring center is in Smith Communications on the second floor.
Exams
- Calculus I -- Spring 2017 -- midterm, Monday March 6.
- Calculus I -- Spring 2017 -- final: Monday May 1, 5 pm, same place.
Each old exam below is a small (<5%) sample of the types of problems that may appear:
- 2016: Calculus I -- Fall 2016 -- midterm, Calculus I -- Fall 2016 -- final
- 2012: Calculus I -- Fall 2012 -- midterm, Calculus I -- Fall 2012 -- final exam
- 2010: Calculus 1: midterm 1, Calculus 1: midterm 2, Calculus 1: final
- 2008: Calculus 1: test 1, Calculus 1: test 2, Calculus 1: test 3, Calculus 1: final exam