Calculus I -- Fall 2016 -- midterm

• Show enough work to justify your answers.
• Write the problems in the given order, each problem on a separate page.

$\bullet$ 1. (a) Represent function $h(x)=e^{x^3-1}$, as a composition of two functions $f$ and $g$. (b) Find its derivative by means of the Chain Rule.

$\bullet$ 2. From the definition, compute the derivative of $f(x)=-x^2-x$ at $a=1$.

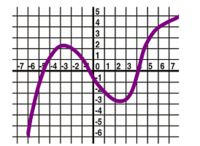
$\bullet$ 3. The graph of a function $f(x)$ is given below. Analyze it (increasing/decreasing, concavity, etc.):

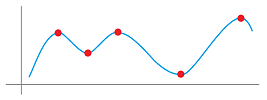
$\bullet$ 4. The graph of function $f$ is given below. Sketch the graph of the derivative $f'(x)$:

$\bullet$ 5. Set up but do not solve an optimization problem for the following question: “What are the dimensions of the rectangle with the smallest possible perimeter and area fixed at $100$?”

$\bullet$ 6. Evaluate $$\frac{d}{dx} \left( \sqrt{x}e^x \right).$$

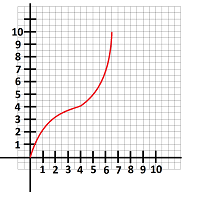
$\bullet$ 7. The graph of a function $f(x)$ is given below. Estimate the values of the derivative $f'(x)$ for $x=1,3$, and $6$.