This site is being phased out.
Calculus 1: final exam
This is a set of sample tests for Calculus 1: course.
1. (a) State the definition of the derivative of a function at point $a$. (b) Use part (a) to compute the derivative of $f(x)=x²+3$ at $a=1$.
2. Find the linear approximation of $f(x)=x^{1/3}$ at $a=1$. Use it to estimate $1.1^{1/3}$.
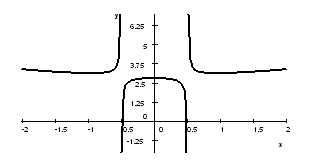
3. The graph of $f$ is given below. Find all the asymptotes of the function and describe them as limits.
4. Suppose $xy+x²y³=1$. Find $\frac{dy}{dx}$.
5. Find the point on the line $y=2-2x$ that is closest to the origin.
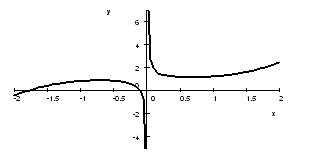
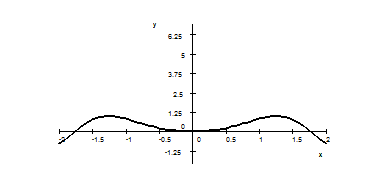
6. The graph of function $f$ is given below. Sketch the graph of the derivative $f′(x)$ in the space under the graph of $f$. Identify all important points and features on the graph.
7. (a) Analyze the function $$f(x)=\frac{x²+7x+3}{x²}$$ and its derivatives. (b) Use part (a) to sketch the graph $f$.
8. (a) State the Fundamental Theorem of Calculus. (b) Use part (a) to evaluate $$\frac{d}{dx}\int_0^{x}e^{t²}dt.$$
9. Evaluate the derivative of of $f(x)=xe^{\sin x}$.
10. The graph of the derivative of function $f$ is given below. Sketch a possible graph of the function $f$ itself in the space under the graph of $f′$. Identify all important points and features on the graph.
11. (a) Make a sketch of the left-end Riemann sums for $\int_0^2\sqrt x\,dx$ with 4 intervals. (b) State the algebraic properties of the Riemann integral.
12. Evaluate $\int_1^2(e^{x}+\sqrt x+x⁻¹)dx.$
13. Evaluate (a) $∫e^{x²}2xdx$; (b) $∫2x\sin (5x)dx$.
Extra credit problem. 5 points, no partial credit. Suppose you are towing a trailer-home. During the first few minutes, every time you look at the rear view mirror you can see only the lower part of the home. Later, every time you look you can see only the top part. Discuss the profile of the road.