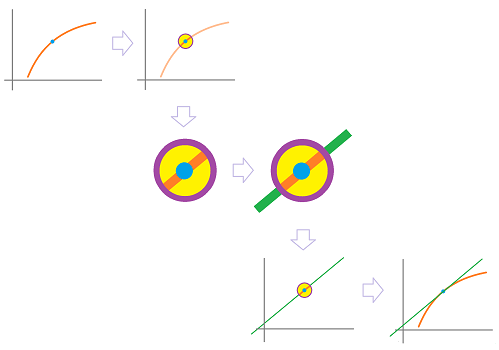
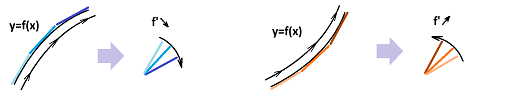This site is being phased out.
Differential calculus
Contents
- 1 Monotonicity, extreme points, and the derivative
- 2 Optimization of functions
- 3 What the derivative says about the difference quotient: The Mean Value Theorem
- 4 Monotonicity and the sign of the derivative
- 5 Concavity and the sign of the second derivative
- 6 Derivatives and extrema
- 7 Anti-differentiation: the derivative of what function?
- 8 Antiderivatives
- 9 The limit of the difference quotient is the derivative
Monotonicity, extreme points, and the derivative
This is how we have been able to solve optimization problems until now.
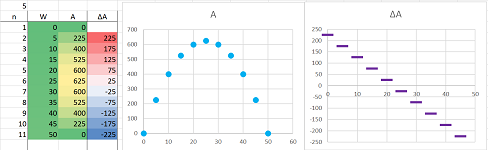
Example. Recall the following problem from Chapter 2: a farmer with $100$ yards of fencing material wants to build as large a rectangular enclosure as possible for his cattle.
We defined the variables, the width $W$ and the area $A$ related by: $$A=W(50-W).$$ Then the problem the problem becomes:
- maximize the function $A(W)=-W^2+50W$.
At its simplest, the solution is examining the data produced by this formula and choosing the largest value from the $A$-column:
Then, the maximal value of the area appears to be $25\cdot 25=625$. What about the monotonicity of the dependence of $A$ on $W$? The solution is, again, examining the data produced by this formula and noticing the pattern of the growth and then decline of the values in the $A$-column. One can also watch the sign of the differences of $A$; the values are increasing when the difference is positive! These are the points where the difference quotients of our function are positive. We conclude that on interval $[0,25]$, the difference quotient is positive and elsewhere is negative.
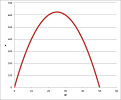
Examining the graph reveals that the maximum value lies somewhere in the area where the graph is the flattest. In other words, this is where the slopes of the secant lines are closest to zero. But these slopes are the difference quotients of our function. Let's find them. From the Power Formula, we have: $$\frac{\Delta A}{\Delta W}=-2W-h+50.$$ We conclude that on interval $[25,25+h]$, the difference quotient is $-h$. This is potentially the number closest to $0$ provided $h$ is small.
Because of the gaps in the data and the graph, we can't completely sure we've found the best answer or that we've fully classified the points:
The problem is solved but let's review the tools at our disposal that allow us to deal with more complex functions. Examining the graph reveals that the maximum value lies somewhere in the area where the graph is the most horizontal. In other words, this is where the slope of the tangent line is zero. But that's the derivative of our function. From the Power Formula, we have: $$\frac{d A}{d W}=-2W+50.$$ We conclude that at $W=25$, the derivative is $0$.
Furthermore, examining the graph reveals that the function is increasing where the slopes of the tangent lines are positive and decreasing where they are negative. In other words, the monotonicity is determined by the sign of slope of the tangent line. We conclude that on interval $(0,25)$, the derivative is positive and on $(25,50)$ it is negative. This analysis amounts to solving the following inequality: $$\frac{dA}{dW}>0\text{ for } W<25.$$ $\square$
How can we find out about any given function whether and where it has monotonicity intervals and its max/min points? The answer we have discovered is with the derivative but we will reach this goal in several stages. First, some background.
We understand increasing functions as ones with graphs rising and decreasing functions as one with graphs falling. We also visualize monotonicity of functions in terms of parts of the graph above or below other part. However, the precise definition must rely on comparing this location to two points at a time.
Recall the definition from Chapter 4.
Definition. Given a function $y=f(x)$ and in interval $I$ within its domain. Then $y=f(x)$ is called increasing on interval $I$ if, for all $a,b$ in $I$, we have: $$\text{if } a\le b \text{ then } f(a)\le f(b);$$ it is called decreasing on interval $I$ if, for all $a,b$ in $I$, we have: $$\text{if } a\le b \text{ then } f(a)\ge f(b).$$ The function is also called strictly increasing and strictly decreasing respectively if these pairs of values cannot be equal; i.e., we replace the non-strict inequality signs “$\le $” and “$\ge $” with strict “$<$” and “$>$”.
When a function is defined on the whole interval, the problem represents a significant challenge (considered in Chapter 4) because drawing such conclusions means comparing infinitely many points.
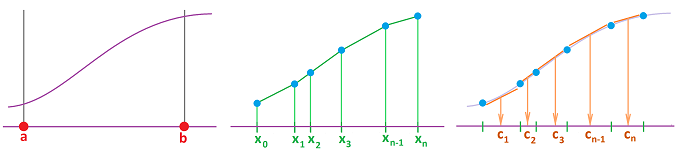
The starting point is, of course, the difference $\Delta f$ and the difference quotient $\frac{\Delta f}{\Delta x}$. Their signs determines whether the function goes up or down from node to node of the partition: $$\begin{array}{|c|}\hline\quad f(x_k) \le f(x_{k+1}) \ \Longleftrightarrow\ \Delta f(c_k) \ge 0 \ \Longleftrightarrow\ \frac{\Delta f}{\Delta x}(c_k) \ge 0. \\ \hline\end{array}$$ The discrete case is solved!
Theorem (Discrete Monotonicity). Suppose a function $f$ is defined at the nodes of a partition of a closed interval. Then,
- $f$ is (strictly) increasing if and only if its difference and the difference quotients are non-negative (positive);
- $f$ is (strictly) decreasing if and only if its difference and the difference quotients are non-positive (negative).
How does this help with the study of monotonicity of functions defined on intervals (the continuous case)? Taking the limit of the difference quotient -- with a particular sign -- will tell us about the sign of the derivative...
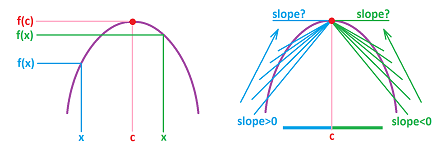
Next, even though we understand maximum and minimum of functions as those locations on the graphs above or below all others, the precise definition must rely, once again, on comparing this location to one point at a time.
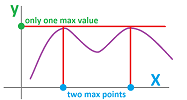
Definition. Given a function $y=f(x)$. Then $x=c$ is called a global maximum point of $f$ on interval $I$ if $f(c)$ is the maximum value of the range of $f$ on $I$, i.e., $$f(c)\ge f(x) \text{ for all } x \text{ in }I;$$ then $y=f(c)$ is called the global maximum value of $f$ on interval $I$. Furthermore, $x=c$ is called a global minimum point of $f$ on interval $I$ if $f(c)$ is the minimum value of the range of $f$ on $I$, i.e., $$f(c)\le f(x) \text{ for all } x \text{ in }I;$$ then $y=f(c)$ is called the global minimum value of $f$ on interval $I$. We call these global extreme points and values, or extrema.
As you see, there can be many max points (those are $x$'s) but only one max value (this is a $y$).
Example. Over the interval $I=(-\infty,+\infty)$, the function $f(x)=\sin x$ has only one global maximum value, $y=1$, but many global maximum points, $$x=\pi /2+2\pi k,\ k=0,\pm 1,\pm 2,...$$
Similarly, the function has only one global minimum value, $y=-1$, but many global minimum points, $$x=-\pi /2+2\pi k,\ k=0,\pm 1,\pm 2, ... $$ The function changes its monotonicity at its extreme points. $\square$
We will limit our attention to continuous functions in order to avoid the situation when these values -- the supremum and the infimum -- are never reached (Chapter 5):
Example (linear polynomials). This is what we know from Chapter 4 about a general linear function: $$\begin{aligned} f(x) &= mx + b, \\ f'(x) & = m. \end{aligned}$$ We derive its monotonicity from the sign of its derivative : $$\begin{array}{lll} m < 0 & \Longrightarrow & mu+b>mv+b \text{ if } u<v& \Longrightarrow &f \text{ strictly decreasing}; \\ m = 0 & \Longrightarrow & mu+b=mv+b \text{ if } u<v& \Longrightarrow &f \text{ constant};\\ m > 0 & \Longrightarrow & mu+b<mv+b \text{ if } u<v& \Longrightarrow &f \text{ strictly increasing}. \end{array}$$ $\square$
Example (quadratic polynomials). Things become much more complex if we need to analyze a quadratic function, $$f(x)=ax^2+bx+c,\ a\ne 0.$$ We recall that all quadratic functions are represented by parabolas (Chapters 3 and 4). They are all result of transformations of the parabola $y=x^2$. What matters especially, is the location of the vertex of the parabola: $$v=-\frac{b}{2a}.$$ The, we have:
- if $a>0$, then $f$ is strictly decreasing on $(-\infty, v)$ and strictly increasing on $(v,+\infty)$;
- if $a<0$, then $f$ is strictly increasing on $(-\infty, v)$ and strictly decreasing on $(v,+\infty)$;
For the first example, the vertex of the parabola is at $$ v = \frac{ 0 + 50 }{ 2 } = 25. $$ We then derive the dynamics of this situation:
- as we increase the width from $0$, the area also increases;
- as the width reaches $25$, the area reaches its maximum value of $625$;
- as we increase the width past $25$, the area starts to decrease.
$\square$
We will next learn how to use the derivative to find the intervals of monotonicity and the extreme points. However, the information about the function's behavior that the derivative (just as any other limit) encodes is local: no matter how small a piece of the graph around $(a,f(a))$ you keep, the derivative $f'(a)$ will remain the same.
We will take an indirect approach. The two definitions below are stepping stones toward the concepts of our main interest given in the two definitions above.
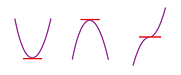
Definition. A function $f$ has an increasing point at $x = c$ if for all $x$ in some open interval $(a, b)$ that contains $c$, we have:
- $f(x) \le f(c)$ for all $x<c$, and
- $f(x) \ge f(c)$ for all $x>c$.
Furthermore, a function $f$ has a decreasing point at $x = c$ if for all $x$ in some open interval $(a, b)$ that contains $c$, we have:
- $f(x) \ge f(c)$ for all $x<c$, and
- $f(x) \le f(c)$ for all $x>c$.
We call these monotone points.
In other words, we have: $$\begin{array}{l|ccc} &x<&c&<x\\ \hline f\nearrow &f(x) \le & f(c) & \le f(x)\\ f\searrow &f(x) \ge & f(c) & \ge f(x)\\ \end{array}$$
Exercise. Does the definition mean that there is an open interval $I$ around $c$ such that $f$ is $f$, restricted to $I$, is increasing or decreasing, respectively?
Next, the extreme points.
Definition. A function $f$ has a local minimum point at $x = c$ if $f(c) \leq f(x)$ for all $x$ in some open interval $I$ that contains $c$. Furthermore, a function $f$ has a local maximum point at $x = c$ if $f(c) \geq f(x)$ for all $x$ in some interval $I$ that contains $c$. We call these local extreme points, or extrema.
In other words, there is an open interval $I$ around $c$ such that $c$ is the global maximum (or minimum) point when $f$ is restricted to $I$.
The connection of these two -- local -- concepts to the previous -- global -- concepts is as follows.
Theorem.
- If a function is increasing (or decreasing) on an open interval $I$, then all points in $I$ are increasing (or decreasing).
- If a function has a global maximum (or minimum) point at $x=c$, on an open interval $I$ then $x=c$ is also a local maximum (or minimum).
Then, the local behavior may reveal the global behavior of the function:
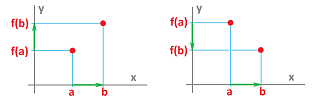
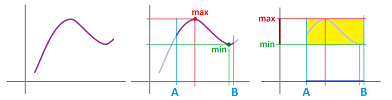
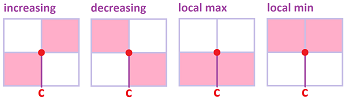
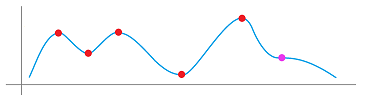
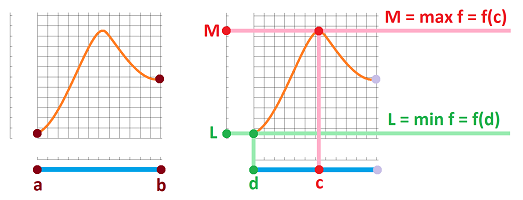
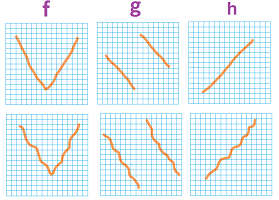
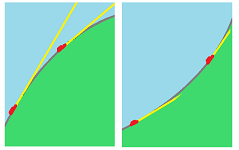
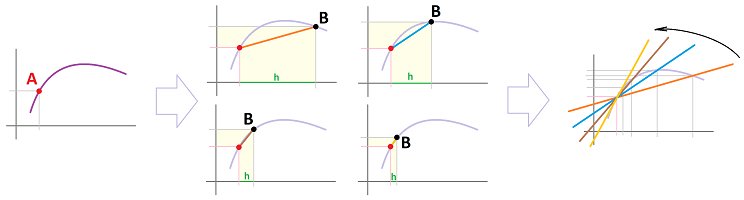
A summary of the two concepts defined above is illustrated below:
The point of interest on the graph is red while the rest of the graph is assumed to be located somewhere in the pink area.
Now, how do we find all these points?
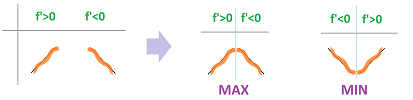
The picture suggests that
- an increasing point $c$ would have an increasing tangent line, i.e., $f'(c) \ge 0$; and
- an extreme point $c$ would have a horizontal tangent line, i.e., $f'(c) = 0$.
The reasoning for the latter is that otherwise we have either $f'(c) > 0$ or $f'(c) < 0$. If we zoom in, the graph merges into the tangent line and we realize there can be no max or min!
Theorem. Suppose a function $y=f(x)$ is differentiable at $x=c$.
- Local Monotonicity Theorem: If $x=c$ is an increasing or decreasing point of $y = f(x)$, then, respectively,
$$f'(c)\ge 0 \text{ or } f'(c)\le 0.$$
- Fermat’s Theorem: If $x=c$ is a local extreme point of $y = f(x)$, then
$$f'(c)=0.$$
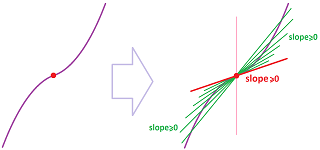
Proof. Let's suppose $c$ is an increasing point. Now, $f'(c)$ is the limit of the slopes of the secant lines through the point $(c,f(c))$.
Consider secant lines within the interval. Then the secant lines both to the left and to the right of $c$ have non-negative slopes: $$\text{slope } = \frac{\overbrace{f(c) - f(x)}^{\ge 0}}{\underbrace{c - x}_{\ge 0}} \ge 0.$$ Apply now the Comparison Theorem for limits: $$g(x) \geq 0\ \Longrightarrow\ \lim\limits_{x \to c} g(x)\geq 0.$$ It follows that $f'(c) \ge 0$.
Next, let's suppose $c$ is a local maximum: $f(c)\ge f(x)$ within some open interval that contains $c$. Again, $f'(c)$ is the limit of the slopes of the secant lines through the point $(c,f(c))$. The idea of the proof is applied but separately for the points to the left and to the right of $c$.
Consider secant lines within the interval. $$\begin{array}{r|c|l} x<&c&>x\\ \hline \text{slopes }\ge 0&&\text{slopes }\le 0\\ \text{therefore }&&\text{therefore}\\ f'(c) \ge 0&\texttt{AND}&f'(c) \le 0\\ 0 \le &f'( c )&\le 0\\ \text{therefore}&&\text{therefore}\\ 0 = &f'( c )&= 0\\ \end{array}$$
For completeness, we demonstrate algebraically that the slopes of these secants have these signs. First, take any (secant) line through $(x, f(x))$ and $(c,f(c))$ with $x < c$. Then $ f(x) \leq f(c)$ when $x$ is close enough to $c$. Why? Because $c$ is a local max (review the definition). Then we have: $$ \text{slope } = \frac{\overbrace{f(c) - f(x)}^{\ge 0}}{\underbrace{c - x}_{> 0}} \ge 0.$$ Second, take any (secant) line through $(x, f(x))$ and $(c,f(c))$ with $x > c$. Then $ f(x) \leq f(c)$ when $x$ is close enough to $c$, because $c$ is a local max. Then we have $$ \text{slope } = \frac{\overbrace{f(c) - f(x)}^{\ge 0}}{\underbrace{c - x}_{< 0}} \le 0.$$
The proof for a minimum is similar. Here is a summary:
$\blacksquare$
Now what about vice versa? Is the converse of Fermat's Theorem true:
- $f'(c) = 0$ then $c$ is a local extreme point of $f$?
It's not true as the example below shows.
Example (zero derivative of $x^3$). Consider $f(x) = x^{3}$ at $x = 0$.
We have: $$f'(x) = 3x^{2} \Longrightarrow f'(0) = 0,$$ but this is not an extreme point. Moreover, it is an increasing point! $\square$
Exercise. How about a “strict” Local Monotonicity Theorem: if $x=c$ is a strictly increasing or strictly decreasing point of $y = f(x)$, then, respectively, $$f'(c)> 0 \text{ or } f'(c)< 0.$$
An alternative terminology is to use
- “absolute” extreme points instead of “global”, and
- “relative” extreme points instead of “local”.
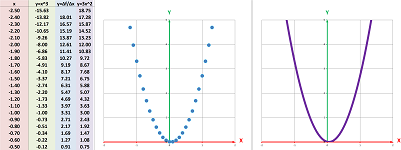
Example. Let's consider a different optimization problem: a square is to be cut from a $10\times 10$ piece of cardboard to create an open box of the largest possible volume.
Let's denote the side of the little square by $x$. Then $x$ becomes the height of the box with the width equal to $10-2x$. Then the volume of the box is $$V=x(10-2x)^2=4x^3-40x^2+100x.$$ The function is cubic! We need to find the largest possible value of this function (for $0\le x \le 5$), but, unfortunately, the completeness of information about parabolas isn't matched by what we know about these functions...
If we plot its graph, we see the highest point within this interval, but, without symmetry to rely on, we can't know its exact value. We know, however, from Fermat's Theorem that we can find this point as one with a zero derivative; i.e., this $x$ satisfies the equation: $$V'=(4x^3-40x^2+100x)'=12x^2-80x+100=4(3x^2-20x+25)=0.$$ Then, from the Quadratic Formula, we have: $$x=\frac{20\pm\sqrt{20^2-4\cdot 3\cdot 25}}{2\cdot 3}=\frac{20\pm 10}{6}=5,\frac{5}{3}.$$ There are no other candidates for this max point! Therefore, the latter one is the answer. We can also confirm that all point between the two are increasing according to the Local Monotonicity Theorem by solving this inequality: $$V'=4(3x^2-20x+25)>0.$$ Indeed, we have the two roots, $5$ and $\frac{5}{3}$, and between them $V'$ will remain negative. $\square$
This is how the monotonicity problem is solved so far: $$\begin{array}{|c|}\hline\quad f(x_k) \le f(x_{k+1}) \ \Longleftrightarrow\ \Delta f(c_k) \ge 0 \ \Longleftrightarrow\ \frac{\Delta f}{\Delta x}(c_k) \ge 0 \ \Longrightarrow\ \frac{df}{dx}\ge 0. \\ \hline\end{array}$$ The last arrow goes in one direction!
Optimization of functions
According to the Fermat's Theorem, the points with zero derivative include all local extrema as well as some other points. We add all of those to our list: the points with zero derivative are candidates for global extreme points.
Example. Let's modify our optimization problem: the corners are to be cut from a $10\times 20$ piece of cardboard to create a closed box of the largest possible volume.
Let $y$ be the width of the box; then $2x+2y=20$, or $y=10-x$. The volume of the box is then: $$V=x(10-2x)(10-x)=2x^3-40x^2+100x,$$ where $x$ is the side of the little square under the restriction $0\le x\le 5$. Plotting the graph (with a spreadsheet) suggests that there is indeed a local maximum.
What is its exact value? According Fermat's Theorem, since the function is differentiable, the point, $c$, has to satisfy $f'(c)=0$. Find the derivative: $$V'(x)=(2x^3-30x^2+100x)'=6x^2-60x+100.$$ Then solve the equation: $$V'(x)=6x^2-60x+100=0,$$ or $$3x^2-30x+50=0.$$ By the Quadratic Formula, we have $$c=\frac{30\pm\sqrt{30^2-4\cdot 3 \cdot 50}}{2\cdot 3}=\frac{30\pm 10\sqrt{3}}{6}.$$ The smaller answer, $c\approx 2.1$, is the maximum. $\square$
So far, our list of candidates for global extreme points of a function are the points where the value of its difference quotient is the closest to zero or, ideally, the points with zero derivative.
Example. Consider $f(x)=\cos x$. First, the difference quotient ($h>0$ is small): $$\frac{\Delta }{\Delta x}(\cos x)=-\frac{ \sin (h/2)}{h/2}\cdot\sin c=0?$$ Second, the derivative: $$\frac{d}{dx}(\cos x)=-\sin x=0?$$ Either equation produces the same list of candidates: $$x=k\pi,\ k=0,\pm 1,\pm 2, ...$$ Just from this fact alone, we can't tell which ones are maxima and which ones are minima. However, we know the following: $$\cos \left( k\pi \right)= \begin{cases} -1& \text{ if } k \text{ is odd},\\ 1& \text{ if } k \text{ is even}. \end{cases}$$ Therefore, the former are the minima and the latter are the maxima. This conclusion confirms what we know about this function:
$\square$
Can there be other candidates for global extrema? If the problem calls for limiting our attention to a closed interval, its end-points cannot be local extrema (and furthermore the derivative isn't defied) because the function is only defined on one side of such a point. We add the two to our list:
- the end-points of the interval are candidates for global extreme points.
The good news is that, we won't miss any extreme values. Indeed, according to the Extreme Value Theorem, a continuous function on a bounded closed interval has a global maximum and a global minimum.
Stripped of all the incidental detail of a word problem, this is what an optimization problem will look like.
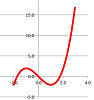
Example. Find global extreme points of $f(x) = x^{3} - 3x$ on $[-2, 3]$.
Step 1: Find the points with zero derivative. Compute: $$ f'(x) = 3x^{2} - 3. $$ Set it to $0$ and solve for $x$. $$\begin{array}{rll} 3x^{2} - 3 &= 0 \quad\Longrightarrow\\ x^{2} &= 1 \quad\Longrightarrow\\ x & = \pm 1. \end{array}$$
Step 2: Compare the values of $f$ at these points and the end-points of the interval, find the smallest and the largest: $$\begin{array}{l|c|lll|c|l} \text{ Candidates}&x&f(x) &= x^{3} - 3x &= x(x^{2} - 3)&y&\text{ classification}\\ \hline f'(x)=0&1&f(1)&= 1(1^{2} - 3)&=&-2& \text{ local and global min }\\ f'(x)=0&-1&f(1)&= -1((-1)^{2} - 3)&=&2& \text{ possibly local but not global max }\\ a&-2&f(-2)&= -2((-2)^{2} - 3)&=&-2 & \text{ global min }\\ b&3&f(3)&= 3(3^{2} - 3)&=&18 & \text{ global max } \end{array}$$
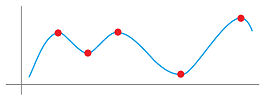
These points and how they are classified are visible on the graph:
$\square$
Are there other candidates? According to the Fermat's Theorem, there are none. The theorem, however, leaves an option of a non-differentiable function.
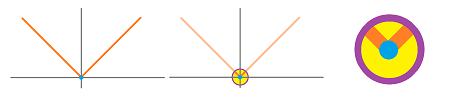
Example. The absolute value function $f(x)=|x|$ has its global minimum at $x=0$; however, it's not differentiable!
In fact, we have: $$f'(x)=\begin{cases} -1& \text{ if }x<0,\\ \text{undefined }& \text{ if }x=0,\\ 1& \text{ if }x>0. \end{cases}$$ Therefore, the global minimum on $[a,b]$ with $a<0<b$ is at $x=0$ and the global maximum at $a$ or $b$. $\square$
Exercise. Consider the derivative and the extreme points of this function:
We have to add those to our list too:
- the points with undefined derivative are candidates for global extreme points.
The points with either undefined or zero derivative are often called “critical points”.
Thus, our list of values of $x$ to be checked is comprised of just two types: the critical points and the end-points. Then, from this list,
- the $x$'s with the largest value of $y$ are the global maxima and
- the $x$'s with the smallest value of $y$ are the global minima.
Example. Analyze the function: $$f(x) = 2x^{3} - 3x^{2} - 12x + 1 $$ on $[-2,3]$.
Compute the derivative: $$f'(x) = 6x^{2} - 6x - 12. $$ Solve the equation: $$\begin{aligned} 6x^{2} - 6x - 12 &= 0 \quad\Longrightarrow\\ x^{2} -x - 2 &= 0 \quad\Longrightarrow\\ \text{QF:} \qquad x &= \frac{1 \pm \sqrt{1 - (-2)4}}{2} \\ &= \frac{1 \pm 3}{2} = 2,1. \end{aligned}$$ Compare: $$\begin{array}{l|c|l|c} \text{ Candidates}&x&f(x) = 6x^{2} - 6x - 12 &y\\ \hline f'(x)=0&2&2\cdot 2^{3} - 3 \cdot 2^{2} - 12 \cdot 2 + 1 = 16 - 12 - 24 + 1 = &-19\\ f'(x)=0&-1&2\cdot (-1)^{3} - 3 \cdot (-1)^{2} - 12 \cdot (-1) + 1 = -2 - 3 +12 + 1 = &8\\ a&-2&2\cdot (-2)^{3} - 3 \cdot (-2)^{2} - 12 \cdot (-2) + 1 = -16 - 12 + 24 + 1 =& -3\\ b&3&2\cdot 3^{3} - 3 \cdot 3^{2} - 12 \cdot 3 + 1 = 54 - 27 -36 + 1 =& -8 \end{array}$$
Answer:
- the global max value is $y = 8$ attained at $x = -1$, a global max point;
- the global min value is $y = -19$ attained at $x = 2$, a global min point.
$\square$
This is a summary of our method.
Theorem (Global extrema). Suppose $f$ is continuous on $[a,b]$ and $c\in [a,b]$ is a global extreme point. Then, one of the following must be satisfied:
- $f'(c)$ is undefined, or
- $f'(c)=0$, or
- $c=a$, or
- $c=b$.
What the derivative says about the difference quotient: The Mean Value Theorem
The Fermat's Theorem is an example of a theorem the converse of which isn't true. This is what it does and does not say about a function differentiable at $x=c$: $$x=c \text{ is }\quad \begin{array}{|l|ll} \text{a local}&\Longrightarrow\\ \text{max/min }&\not\Longleftarrow \end{array} \quad \begin{array}{|c|}\hline \quad f'(c)=0 \quad \\ \hline\end{array}.$$ The converse of the Local Monotonicity Theorem is true but hasn't been proved yet: $$x=c \text{ is }\quad \begin{array}{|l|ll} \text{an increasing}&\Longrightarrow\\ \text{point }&\Longleftarrow \end{array} \quad \begin{array}{|c|}\hline \quad f'(c)\ge 0 \quad \\ \hline\end{array}.$$
There are other statements in the converses of which we are interested:
- the derivative of a constant function is zero, but are the constants the only functions with this property?
- the derivative of a linear polynomial is constant, but are the linear polynomials the only functions with this property?
- the derivative of a quadratic polynomial is linear, but are the quadratic polynomials the only functions with this property?
The first question asks if we can build a curve -- other than a horizontal line -- with all tangent lines horizontal. Try it!
Answering Yes to the last two questions justifies our solution, $$y(t)=y_0+v_0t-\frac{1}{2}gt^2,$$ of the problem of free fall as presented in Chapter 8: $$\text{constant force}\ \Longrightarrow\ \text{constant acceleration}\ \Longrightarrow\ \text{linear velocity}\ \Longrightarrow\ \text{quadratic location}.$$
The main theorem of this section will help with these and other questions.
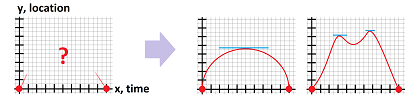
Example (driving). Let's interpret the conclusion of Fermat's Theorem in terms of motion:
- $x$ is time,
- $f(x)$ is the location at time $x$,
- $f'(x)$ is the velocity at time $x$.
First, we need to assume that the velocity always makes sense: there are no sudden changes of direction, bumps, or crushes (and no teleportation!). Then we conclude that
- $(\Rightarrow )$ whenever we are the farthest from home or any location, we stop, at least for an instant.
But not conversely:
- $(\not\Leftarrow )$ even if we stop, we can resume driving in the same direction.
Imagine that you:
- left home at $1$ pm,
- did some driving,
- came home at $2$ pm.
Question: What can one infer about your speed during this time? For simplicity, we assume that you drove on a straight road...
You may have driven slowly, then fast, but one thing is certain: you came back home. And to come back, you had to turn around. And to turn around, you had to stop. So, speed = $0$ at least once! $\square$
Let's make the observation in the last example purely mathematical and turn it into a theorem.
Theorem (Rolle's Theorem). Suppose
- 1. $f$ is continuous on $[a,b]$,
- 2. $f$ is differentiable on $(a,b)$,
- 3. $f(a) = f(b)$.
Then $f'(c) = 0$ for some $c$ in $[a,b]$.
We again assume that $x$ is time, limited to interval $[a,b]$. In the theorem, #1 means that you don't leap, #2 means that don't crash, #3 means that you've come back. We already know that this special point in time was when you were farthest away from home (in either direction); you weren't moving then.
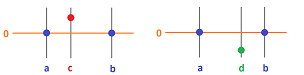
Proof. Suppose $f$ has on $[a,b]$:
- a global maximum at $x = c$ and
- a global minimum at $x = d$.
These assumptions are justified by the Extreme Value Theorem (that's why we need to assume continuity).
Case 1: either $c$ or $d$ is not an end-point, $a$ or $b$. We now use the Fermat's Theorem: every global extreme point has $0$ derivative when it's not an end-point. It follows that $f'(c) = 0$ or $f'(d) = 0$, and we are done.
Case 2: both $c$ and $d$ are end-points, $a$ or $b$. Then $$\left.\begin{aligned} f(c) & = f(a) \qquad \text{ or } \qquad f(c) = f(b) \\ f(d) & = f(a) \qquad \text{ or } \qquad f(d) = f(b) \end{aligned} \right\} \qquad \text{But these are equal!} $$ Therefore, $$f(c) = f(d).$$ But this means that $$\max f= \min f !$$ Therefore $f$ is constant on $[a,b]$, so $f'(x) = 0$ for all $x$ in $(a,b)$. $\blacksquare$
The condition of the theorem simply states that the difference quotient is zero, $$\frac{\Delta f}{\Delta x}=0,$$ where the partition of $[a,b]$ is trivial: $n=1,\ x_0=a,\ x_1=b$.
Thus, Rolle's Theorem says that if you passed the same location twice, you must have stopped at some moment during this time. The former condition, $$f(a)=f(b),$$ can be rewritten as: $$f(b)-f(a)=0.$$ Other interpretations of this are:
- the change of the function over the interval is zero, or
- the rise over the interval is zero, or
- the displacement over the time interval is zero.
Then the difference quotient is also zero: $$\frac{f(b)-f(a)}{b-a}=0.$$ Other interpretations of this are:
- the average rate of change over the interval is zero, or
- the slope of the secant line is zero, or
- the average velocity over the time interval is zero.
Thus, Rolle's Theorem says:
- the average rate of change is zero $\Longrightarrow$ the instantaneous rate of change is zero at some point; or
- the slope of the secant line is zero $\Longrightarrow$ the slope of the tangent line is zero at some point; or
- the average velocity is zero $\Longrightarrow$ the instantaneous velocity is zero at some point.
Now, do the hypothesis and the conclusion have to be about a zero velocity? Can it be $100$ m/h?
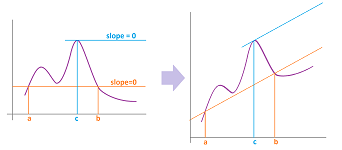
What happens if we rotate (or skew) the graph?
The picture suggests what happens to the entities we considered in Rolle's theorem:
- the tangents of those special points that used to be horizontal have become inclined;
- the secant line that connects the end-points that used to be horizontal has become inclined.
But these lines are still parallel!
So, we need to connect these two:
- the slopes of the tangents line on $(a,b)$ (that's the velocity) and
- the slope of the line between $(a,f(a))$ and $(b,f(b))$ (that's the average velocity on $[a,b]$).
Example. To illustrate the idea, let's revisit the issue of speeding.
A radar gun catches the instantaneous speed of the car. By law it shouldn't be above $70$ m/h. When the radar gun shows anything above, you're caught.
Now, suppose there is no radar gun. Imagine instead that a policeman observed you driving by (at a legal speed) and then, after $1$ hour, another policeman observed you driving by -- but $100$ miles away!
Then the average speed of yours was $100$ m/h. Did you violate the law? Considering that no-one can testify to have seen you drive above the speed limit, can the two policemen compare notes and prove that you did?
The analysis we pursue here allows them to infer that yes, your instantaneous velocity was $100$ m/h at some point. To make their case against you rock-solid, they'd use the theorem below. $\square$
Theorem (Mean Value Theorem). Suppose
- 1. $f$ is continuous on $[a,b]$,
- 2. $f$ is differentiable on $(a,b)$.
Then $$\frac{f(b) – f(a)}{b-a} = f'(c),$$ for some $c$ in $(a,b).$
What happens if in MVT, $f(a) = f(b)$? Then the left-hand side is $0$, hence $0 = f'( c)$. We have the conclusion of Rolle's Theorem. This means that MVT is more general than RT. In other words, the latter is an instance, a narrow case of MVT.
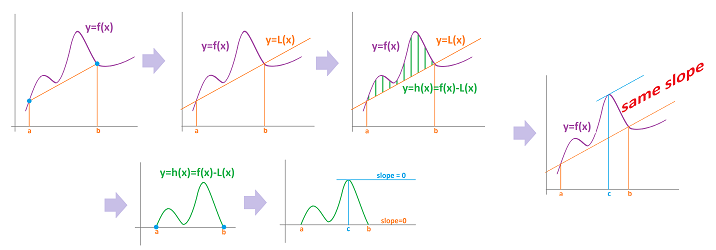
The proof of MVT however will rely on RT. The idea is to “skew” the graph of MVT back to RT. This is the outline of the proof:
Proof. Let's rename $f$ in Rolle's Theorem as $h$ to use it later. Then its conditions take this form:
- 1. $h$ continuous on $[a,b]$.
- 2. $h$ is differentiable on $[a,b]$.
- 3. $h(a) = h(b) $.
Suppose $y=L(x)$ is the linear function represented by the line between $(a,f(a))$ and $(b,f(b))$. Then, its derivative is simply its slope: $$L'(x)=\frac{f(b) – f(a)}{b-a}.$$
Now back to $f$. This is the key step; let $$h(x) = f(x) – L(x).$$ Let's verify the conditions above.
First, $h$ is continuous on $[a,b]$ as the difference of the two continuous functions (SR). Condition #1 above is satisfied!
Next, $h$ is differentiable on $(a,b)$ as the difference of the two differentiable functions (SR). Condition #2 above is satisfied! The derivative is simple: $$h'(x)=f'(x)-\frac{f(b) – f(a)}{b-a}.$$
We also have: $$f(a) = L(a), \ f(b) = L(b)\ \Longrightarrow\ h(a) = 0,\ h(b) = 0\ \Longrightarrow\ h(a) = h(b).$$ Condition #3 above is satisfied!
Thus, $h$ satisfies the conditions of RT. Therefore, the conclusion is satisfied too: $$h'(c)=0$$ for some $c$ in $(a,b)$. In other words, we have $$f'(c)-\frac{f(b) – f(a)}{b-a}=0.$$ $\blacksquare$
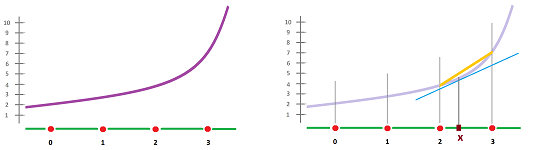
Geometrically, $c$ is found by shifting the secant line until it touches the graph:
In the following sections, we will use the Mean Value Theorem to derive facts about the function from the a priori facts about its derivative, especially the converses mentioned in the last section.
Monotonicity and the sign of the derivative
What a priori information about the derivative of a function tell us about its monotonicity?
Recall that the Local Monotonicity Theorem states that, for a function $y=f(x)$ differentiable at $x=c$, if $x=c$ is an increasing point of $y = f(x)$, then $f'(c)\ge 0$. Instead of proving the converse of this local result, we will use the Mean Value Theorem to prove a global result! We include the discrete case for completeness.
Theorem (Monotonicity Theorem). (A) Suppose $f$ is defined at the nodes of a partition on a closed interval $I$. Then,
- $\frac{\Delta f}{\Delta x}\ge 0$ on $I$ if and only if $f$ is increasing on $I$;
- $\frac{\Delta f}{\Delta x}\le 0$ on $I$ if and only if $f$ is decreasing on $I$.
(B) Suppose $f$ is differentiable on an open interval $I$. Then,
- $f' \ge 0$ on $I$ if and only if $f$ is increasing on $I$;
- $f' \le 0$ on $I$ if and only if $f$ is decreasing on $I$.
Proof. $(\Leftarrow)$ If $f$ is increasing on $I$, every point $c$ in $I$ is an increasing point of $f$. Therefore, by the Local Monotonicity Theorem, we have $f'(c)\ge 0$.
$(\Rightarrow)$ Suppose $a,b$ are in $I$ and $a<b$. We need to show that $f(a) \le f(b)$. By the Mean Value Theorem, we have: $$\frac{f(b)-f(a)}{b-a} = f'(c)$$ for some $c$ in $(a,b)$. No matter what $c$ is, by assumption of the theorem, the right-hand side is non-negative. Therefore, we have $$\frac{f(b) – f(a)}{b-a} \ge 0.$$ Now observe that in this fraction, the denominator is $b-a > 0$. Therefore, the numerator must be also positive: $f(b) – f(a) \ge 0$. Hence, $f(b) \ge f(a)$. $\blacksquare$
Example. We use the derivatives to analyze these functions: $$\begin{array}{llll} (1)&f(x)=3x^2+1\ &\Longrightarrow\ &f'(x)=6x+3\ &\Longrightarrow\ \\ &f'(x)<0 \text{ if } x < 0 &\text{ and }& f'(x)>0 \text{ if } x> 0 \ &\Longrightarrow\ \\ & f\searrow \text{ on } (-\infty,-0) &\text{ and }& f\nearrow \text{ on } (0,\infty);\\ \\ (2)&g(x)=\frac{1}{x}\ &\Longrightarrow\ &g'(x)=-\frac{1}{x^2}\ &\Longrightarrow\ \\ &g'(x)<0 \text{ if } x < 0 &\text{ and }& g'(x) <0 \text{ if } x> 0 \ &\Longrightarrow\ \\ & g\searrow \text{ on } (-\infty,0) &\text{ and }& g\searrow \text{ on } (0,\infty);\\ \\ (3)&h(x)=e^x\ &\Longrightarrow\ &h'(x)=e^x\ &\Longrightarrow \\ &h'(x)>0 \text{ for all } x \ &\Longrightarrow\ \\ & h\nearrow \text{ on } (-\infty,\infty). \end{array}$$ With just this data, we can sketch very rough graphs of these three functions:
Even though we have shown that the functions have no other extrema, the curves could possibly “wiggle”. This issue will be addressed shortly. $\square$
Example. Recall this example: $$f(x) = x^{3} - 3x, $$ on what intervals is it increasing and decreasing?
First, $$f'(x) = 3x^{2} - 3.$$ In order to use the Monotonicity Theorem, we need to find those $x$'s that produce $f'(x) > 0$ or $f'(x) < 0$. In other words, we need to solve these inequalities.
We start with the corresponding equation $f'(x) = 0$, done previously: $$\begin{aligned} 3x^{2} - 3 &= 0 \ \Longrightarrow\ \\ x^{2} - 1 &= 0\ \Longrightarrow\ \\ x^{2} &= 1\ \Longrightarrow\ \\ x & = \pm 1. \end{aligned}$$ We have three intervals
- 1. $(-\infty, -1),$
- 2. $(-1,1),$
- 3. $(1,\infty).$
We need to know the sign of the derivative on each.
Since $f'$ is continuous, the sign of $f'$ can only change at $-1$ or $1$. Therefore, we just need to sample one point within each interval to the sign of the derivative on the whole interval:
- 1. Pick $x = -2$, then $f'(-2) = 3 \cdot (-2)^{2} -3 = 9 > 0$. Then $f'(x) > 0$ for $x$ in $(-\infty, -1)$. Therefore, $f \nearrow$ on $(-\infty,-1)$.
- 2. Pick $x = 0$, then $f'(0) = -3 < 0$. Then $ f'(x) <0$ for $x$ in $(-1,1)$. Therefore, $f \searrow$ on $(-1,1)$.
- 3. Pick $x=2$, then $f'(2) = 3 \cdot 2^{2} - 3 = 9 > 0$. Then $f'(x) >0$ for $x$ in $(1,\infty)$. Therefore, $f \nearrow$ on $(1,\infty)$.
Let's put this data in a table: $$\begin{array}{cccc} x:&(-\infty,-1)&(-1,1)&(1,\infty)\\ f:& \nearrow&\searrow&\nearrow \end{array}$$ These arrows are close to forming a curve, especially after this modification: $$\begin{array}{cccc} &&\cdot&&\\ f:&\nearrow&&\searrow&&\nearrow\\ &&&&\cdot&\\ x:&&-1&&1&&1 \end{array}$$ Note that we have also -- automatically -- classified the extreme points!
We confirm the result by plotting:
$\square$
Example. Consider $f(x)=\sin x$ again. We already know that the difference quotient and the derivative are zero, $\cos x=0$, at these locations: $$x=\tfrac{\pi}{2}+k\pi,\ k=0,\pm 1,\pm 2, ...$$ These are the points where the difference quotient and the derivative could, potentially, change their sign! Since the two differ by a positive multiple: $$\frac{\Delta }{\Delta x}(\cos x)=-\frac{ \sin (h/2)}{h/2}\cdot\sin x=\frac{ \sin (h/2)}{h/2}\cdot\frac{d}{dx}(\cos x),$$ they change signs together. From what we know even more about cosine, the sign does change every time: $$\begin{array}{rccc} &&&\cdot&&&&\cdot&&&&\cdot&&\\ y=\sin x:&&\nearrow&&\searrow&&\nearrow&&\searrow&&\nearrow\\ &\cdot&&&&\cdot&&&&\cdot\\ x:&-\pi/2&&\pi /2&&3\pi/2&&5\pi/2&&7\pi/2&&9\pi/2\\ y=\cos x:&0&+&0&-&0&+&0&-&0&+&0&- \end{array}$$
This conclusion confirms what we know about this function:
$\square$
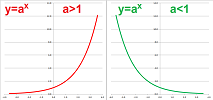
Example. Let's consider the exponential function $f(x)=a^x$ for all $a>0$. First the derivatives: $$f'(x)=\left( a^x \right)'=a^x \ln a.$$ Therefore, by the Monotonicity Theorem, for all $x$ we have:
- $a>1 \ \Longrightarrow\ f'(x)>0$;
- $0<a<1 \ \Longrightarrow\ f'(x)<0$.
It follows that the function is either all increasing or all decreasing:
Then, when $a>1$, we have the global minimum on interval $[a,b]$ at $x=a$ and the global maximum at $b$. $\square$
Example. Let's consider $f(x)=x^3$.
The derivative is $f'(x)=3x^2$. Therefore, by the Monotonicity Theorem, we have: $$\begin{array}{lll} \text{on }(-\infty,0)&f'>0&\Longrightarrow\ &f\nearrow,\\ \text{at }0&f'=0,&\\ \text{on }(0,+\infty)&f'>0&\Longrightarrow\ &f\nearrow. \end{array}$$ Are we done? The picture suggests that there is more here. We can see, and we demonstrated previously, that $f(x)=x^3$ is increasing throughout its domain! Thus, we have an example of a function with these properties:
- $f\nearrow$ on $(-\infty,+\infty)$, even though
- $f'(0)=0$.
$\square$
This is a modified version of our theorem.
Theorem (Strict Monotonicity). (A) Suppose $f$ is defined at the nodes of a partition on a closed interval $I$. Then,
- $\frac{\Delta f}{\Delta x}> 0$ on $I$ if and only if $f$ is increasing on $I$;
- $\frac{\Delta f}{\Delta x}< 0$ on $I$ if and only if $f$ is decreasing on $I$.
(B) Suppose $f$ is differentiable on an open interval $I$. Then,
- if $f' > 0$ on $I$ then $f$ is strictly increasing on $I$;
- if $f' < 0$ on $I$ then $f$ is strictly decreasing on $I$.
Proof. Just replace each “$\ge$” in the proof of the Monotonicity Theorem with “$>$”. $\blacksquare$
We demonstrated in the last example that the converse fails.
Exercise. Show that if the derivative of a function is zero, it is a constant function, in two ways: (a) by modifying the proof of the Monotonicity Theorem, (b) by applying the Monotonicity Theorem.
Corollary (One-to-one). Suppose $f$ is differentiable on an open interval $I$. Then, if $f' > 0$ on $I$ or $f' < 0$ on $I$ then $f$ is one-to-one on $I$.
Exercise. Prove the corollary. What about the converse?
Concavity and the sign of the second derivative
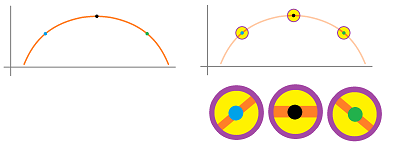
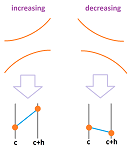
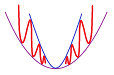
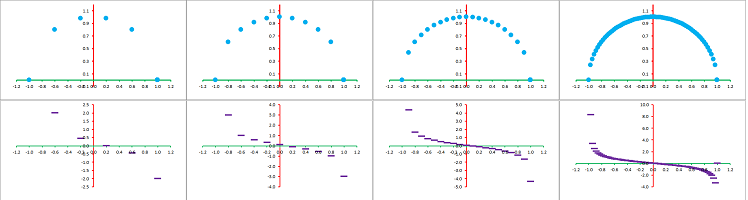
Recall how we saw the simple idea behind monotonicity by zooming in on the graph made of overlapping dots:
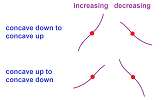
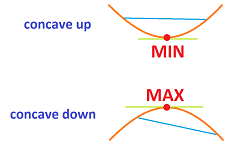
We will do the same for a subtler idea. The picture below informally reveals the meaning of upward and downward concavity:
When we guarantee the one or the other, we eliminate the possibility of “wiggly” curves! We will also be able to tell maxima from minima.
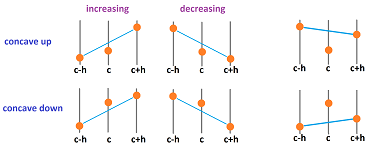
Let's zoom in. There are three points this time:
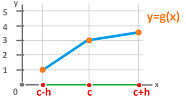
The pattern is clear: it is concave up when the middle point lies below the line connecting the other two and concave down when it is above.
Let's investigate the algebra. The two points on the $y$-axis are $f(c-h)$ and $f(c+h)$.
Therefore, the $y$-value of the mid-point is their average: $$\frac{f(c-h)+f(c+h)}{2}.$$ Then the concave up and concave down conditions take the form of these inequalities respectively: $$f(c) \le \frac{f(c-h)+f(c+h)}{2} \quad\text{ and }\quad f(c) \ge \frac{f(c-h)+f(c+h)}{2}.$$ What does this have to do with the derivatives? We re-arrange the terms of the former: $$f(c+h)-2f(c)+f(c-h) \ge 0,$$ and, furthermore, we see two differences: $$\big[ f(c+h)-f(c) \big] - \big[ f(c)-f(c-h) \big] \ge 0,$$ or, if we assume the mid-point secondary nodes, $$\Delta f(c+h/2)-\Delta f(c-h/2) \ge 0.$$ This is the difference of differences!
It only takes division by $h>0$, twice, $$\frac{ \frac{\Delta f(c+h/2)}{h}-\frac{\Delta f(c-h/2)}{h} }{h} \ge 0,$$ to arrive to the difference quotient of the difference quotient at $x=c$: $$\frac{\Delta^2 f}{\Delta x^2}(c) \ge 0.$$ This is the second difference quotient.
What if the points aren't equally spaced? We will use a stronger restriction.
Definition. Suppose three consecutive nodes $x_{i-1},x_i,x_{i+1}$ of a partition satisfy $$x_i=\alpha x_{i-1}+\beta x_{i+1},$$ and $$f(x_i) \le \alpha f(x_{i-1})+\beta f(x_{i+1}),$$ for some pair $\alpha\ge 0$ and $\beta\ge 0$ with $\alpha +\beta =1$. Then the function $f$ is called concave up at $x_i$. When the opposite inequality is satisfied the function $f$ is called concave down.
Theorem (Discrete concavity). Suppose a function $f$ is defined at the nodes of a partition of interval $[a,b]$. Then,
- (1) $f$ is concave up on $[a,b]$ if and only if $\frac{\Delta^2 f}{\Delta x^2} \ge 0$;
- (2) $f$ is concave down on $[a,b]$ if and only if $\frac{\Delta^2 f}{\Delta x^2} \le 0$.
Proof. The first equation indicates that $\alpha$ and $\beta$ give us the relative position of $x_i$ within the interval $[x_{i-1},x_{i+1}$]. Furthermore, $\alpha f(x_{i-1})+\beta f(x_{i+1})$ is at the same relative position within the interval between $f(x_{i-1})$ and $\beta f(x_{i+1})$. When $\Delta x_{i-1}=\Delta x_{i}$ and $\alpha=\beta=1/2$, the definition produces the above inequalities.
The sign of the difference quotient or the derivative will tell us the difference between increasing and decreasing behavior. We need to develop another calculus tool to evaluate the concavity.
Let's first find $\alpha$ and $\beta$. Consider the first equation of the definition re-written: $$x_i=\alpha (x_{i}-\Delta x_{i-1})+\beta (x_{i}+\Delta x_i).$$ Cancellation produces the following: $$0=\alpha (-\Delta x_{i-1})+\beta (\Delta x_i).$$ Therefore, $$\alpha=\frac{\Delta x_{i}}{\Delta x_{i-1}+\Delta x_{i}},\ \beta=\frac{\Delta x_{i-1}}{\Delta x_{i-1}+\Delta x_{i}}.$$
The concavity is determined by the sign of the following expression: $$\alpha f(x_{i-1})+\beta f(x_{i+1})-f(x_i) \ge 0.$$ What is its meaning? We substitute $\alpha$ and $\beta$ and our expression becomes: $$\frac{\Delta x_{i}}{\Delta x_{i-1}+\Delta x_{i}} f(x_{i-1})+\frac{\Delta x_{i-1}}{\Delta x_{i-1}+\Delta x_{i}} f(x_{i+1})-f(x_i) \ge 0.$$ Let's rearrange the terms: $$\Delta x_{i} f(x_{i-1})+\Delta x_{i-1} f(x_{i+1})-(\Delta x_{i-1}+\Delta x_{i})f(x_i) \ge 0,$$ and factor: $$\Delta x_{i-1}\big( f(x_{i+1})-f(x_i)\big)-\Delta x_{k}\big(f(x_i)-f(x_{i-1})\big) \ge 0.$$ In parentheses we see the two differences of $f$ evaluated at the two adjacent intervals $[x_{i-1},x_i],[x_i,x_{i+1}]$. To see the difference quotients, let's divide this by $\Delta x_{i-1}\Delta x_{i}$: $$\frac{ f(x_{i+1})-f(x_i)}{\Delta x_{i}}-\frac{f(x_i)-f(x_{i-1})}{\Delta x_{i-1}} \ge 0\ \text{ or }\ \frac{\Delta f}{\Delta x}(c_i)-\frac{\Delta f}{\Delta x}(c_{i-1}) \ge 0.$$ It only takes division by $\Delta c_i$ to arrive to the difference quotient of the difference quotient: $$\frac{\Delta^2 f}{\Delta x^2}(x_i) \ge 0.$$ $\blacksquare$
Example. This is how the second difference quotient is computed with a spreadsheet:
The transition from $f$ to $\frac{\Delta f}{\Delta x}$ and from $\frac{\Delta f}{\Delta x}$ to $\frac{\Delta^2 f}{\Delta x^2}$ are implemented with the same formula. $\square$
Now, to the continuous case. A function is concave when any of samplings is; i.e., the segments of the secant lines (“cords”) lie either above or below the graph.
Definition. If for each $x$ in $I$, each $k,h>0$, and any pair of positive $\alpha$ and $\beta$ with $\alpha +\beta =1$, we have $$f(x) \le \alpha f(x-k)+\beta f(x+h),$$ within the interval $I$, then the function $f$ is called concave up on interval $I$. When the opposite inequality is satisfied the function $f$ is called concave down on interval $I$. The function is strictly concave (up or down) if the inequality is strict.
Exercise. Is a linear function concave up or down?
We will use the notation:
- $\smile$ for concave up, and
- $\frown$ for concave down.
Theorem (Concavity Theorem). Suppose a function $f$ is twice differentiable on an open interval $I$. Then,
- (1) if $f' ' \ge 0$ on $I$, then $f$ is concave up on $I$;
- (2) if $f' ' \le 0$ on $I$, then $f$ concave down on $I$.
Proof. If $f' ' \ge 0$ on $I$, then by the Monotonicity Theorem, $f'$ is increasing. Therefore, $$f'(s) \le f'(t)$$ for all $s<t$ in $I$. Now by the Mean Value Theorem, we have: $$\frac{f(c)-f(c-h)}{h}=f'(s)$$ for some $s$ in $(c-h,c)$, and $$\frac{f(c+h)-f(c)}{h}=f'(t)$$ for some $t$ in $(c,c+h)$. Therefore, $$\big(f(c-h)+f(c+h\big)-2f(c) =h\left( \frac{f(c+h)-f(c)}{h}-\frac{f(c)-f(c-h)}{h}\right)=h(f'(t)-f'(s)) \ge 0.$$ $\blacksquare$
Exercise. Derive the theorem from the theorem about discrete concavity in this section.
Example. (1) $$\begin{array}{lll} f(x)&=3x^2+1\ \Longrightarrow\ \\ f'( x )&=6x\ \Longrightarrow\\ f' '(x)&=6.\\ f' '(x)>0\ & \Longrightarrow\ f \smile. \end{array}$$
(2) $$\begin{array}{lll}g(x)&=\frac{1}{x}\ \Longrightarrow\ \\ g'( x )&= -\frac{1}{x^2} \text{ for } x\ne 0\ \Longrightarrow\\ g' '(x)&=\frac{1}{2x^3} \text{ for } x\ne 0\ .\\ g' '(x)<0 \text{ for } x< 0 &\Longrightarrow\ g \frown \text{ on } (-\infty,0);\\ g' '(x)>0 \text{ for } x>0 &\Longrightarrow\ g \smile \text{ on } (0,\infty). \end{array}$$
(3) $$\begin{array}{lll} h(x)&=e^x\ \Longrightarrow\ \\ h'( x )&= e^x \Longrightarrow\ \\ h' '(x)&=e^x. \\ h' '(x)>0 &\Longrightarrow\ h \smile. \end{array}$$
Using this data combined with the increasing/decreasing behavior established earlier, we can sketch by hand the graphs of these three functions:
$\square$
Definition. The points where the function changes its concavity are called inflection points; i.e., these are such points $c$ that the function's concavity on some interval $(a,c)$ is opposite of the concavity on some interval $(c,b)$.
Warning: The value of the first derivative at inflection points can be arbitrary; it is $0$ for $f(x)=x^3$ at $0$ and non-zero for the trigonometric functions below.
Example. If we use the Trig Formulas: $$\begin{array}{lllll} (\sin x)'= \cos x,\\ (\cos x)'=-\sin x. \end{array}$$ twice, we have $$\begin{array}{lllll} (\sin x)' '= - \sin x,\\ (\cos x)' '= -\cos x. \end{array}$$ As we know, the two functions alternate -- periodically every $\pi$ -- between positive and negative values: $$\begin{array}{ccc} +&0&-&+&0&-&0&+&0- \end{array}$$ Therefore, the two functions alternate -- periodically every $\pi$ -- between concave up and concave down behavior: $$\begin{array}{ccc} &\cdot &&&&\cdot&&&&\cdot&&&&\ \\ \nearrow &\frown& \searrow &\smile&\nearrow&\frown& \searrow &\smile& \nearrow &\frown& \searrow &\smile&\\ &&&\cdot&&&&\cdot&&&&\cdot&&&& \end{array}$$ These are the inflection points of the function. $\square$
When using the Monotonicity Theorem, we compare
- the shapes of the patches of the graph of the function $f$, $\searrow$ or $\nearrow$, to the signs of the values of the first derivative $f'$, $+$ or $-$.
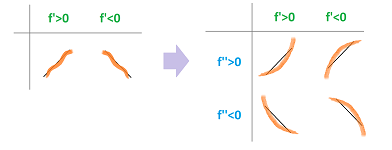
Meanwhile, when using the Concavity Theorem, we compare
- the shapes of the patches of the graph of the function $f$, $\smile$ or $\frown$, to the signs of the values of the second derivative $f' '$, $+$ or $-$.
One can see how we use a higher level of analysis in comparison to the first derivative (the wiggles are gone!):
Warning: as the second diagram indicate, monotonicity and concavity are two independent characteristics of a function; one should never try to figure out one from the other.
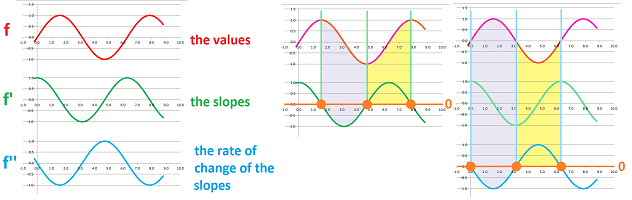
The conclusion of the Concavity Theorem is seen from the following. As the first derivative represents the slopes of the function, the second derivative represents the rate of change of these slopes. As you can see, the slopes increase when the lines are rotated in the counter-clockwise direction:
Therefore, the tangent lines rotate as follows:
- decreasing slopes $\Longrightarrow$ tangent lines rotate clockwise;
- increasing slopes $\Longrightarrow$ tangent lines rotate counter-clockwise.
We can see this if we imagine how we drive on this road:
Even though we are climbing in either case, what happens to the beams is different:
- when the road is concave down, the headlights point up above the road and, therefore, the beams are turning clockwise; while
- when the road is concave up, the headlights point down into the road and, therefore, the beams are turning counter-clockwise.
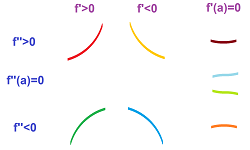
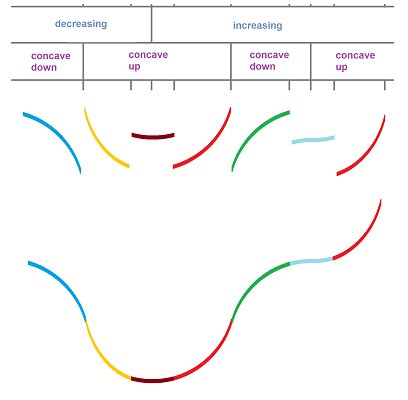
All graphs are made of the following eight pieces classified according to the sign of the derivative and the second derivative:
Example. Below, we start with the information about monotonicity and concavity of a function on several intervals, then pick appropriate pieces from the above table, and then glue them together to form a continuous curve:
$\square$
Here is yet another way to interpret the terminology and the notation: $$\begin{array}{c|c} \text{ “feeling up” }& \text{ “feeling down” } \\ \ddot{\smile} & \ddot{\frown} \end{array}$$
Derivatives and extrema
Recall what the Fermat's Theorem does and does not say about a function differentiable at $x=c$: $$x=c \text{ is }\quad \begin{array}{|l|ll} \text{a local}&\Longrightarrow\\ \text{max/min }&\not\Longleftarrow \end{array} \quad \begin{array}{|c|}\hline \quad f'(c)=0 \quad \\ \hline\end{array}.$$ When can we reverse the arrow? These are the three possibilities:
It is impossible to tell one from the other without looking at the derivative in the vicinity of the point!
Example. Consider again: $$f(x) = x^3 - 3x. $$ We know that $f'(x) = 0$ for $x = \pm 1$ and none others. The derivative is $0$, so these may be extreme points. How do we know? We look at the signs of the derivative:
- $f' > 0$ and $f\nearrow$ to the left of $-1$,
- $f' < 0$ and $f\searrow$ to the right of $-1$.
This can only happen when $x=-1$ is a local max. The opposite for $x = 1$. Indeed:
$\square$
The general result is the following.
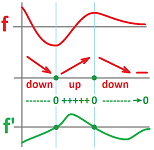
Theorem (First Derivative Test). If the derivative changes its sign at a point, the point is an extremum. Suppose $f$ is differentiable on an open interval $I$ that contains point $x=c$. Then,
- if $f'(x)\ge 0$ for all $x<c$ and $f'(x)\le 0$ for all $x>c$ within $I$, then $c$ is a local maximum point;
- if $f'(x)\le 0$ for all $x<c$ and $f'(x)\ge 0$ for all $x>c$ within $I$, then $c$ is a local minimum point.
Proof. Suppose $I=(a,b)$. If $f'(x)\ge 0$ for all $a<x<c$, then by the Monotonicity Theorem, $f(x)\le f(c)$ for all $a<x<c$. If $f'(x)\le 0$ for all $c<x<b$, then by the Monotonicity Theorem, $f(x)\le f(c)$ for all $c<x<b$. Thus, $f(x)\le f(c)$ for all $a<x<b,\ x\ne c$. Then, $c$ is a local maximum. $\blacksquare$
In other words,
- if $f'(x)$ changes its sign at $x=c$ from $+$ to $-$, then $c$ is a local maximum point;
- if $f'(x)$ changes its sign at $x=c$ from $–$ to $+$, then $c$ is a local minimum point.
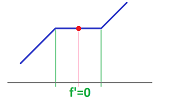
Example. The converse fails as the following example shows:
$\square$
Exercise. Devise a formula for the above function and show that the converse of the theorem fails.
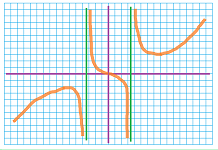
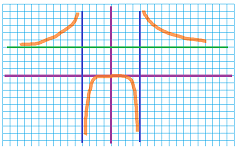
Example. Let's analyze this function: $$f(x)=\frac{x^3}{x^2-3}.$$
First, the domain is all $x$ except $\pm\sqrt{3}$.
Next, we differentiate: $$\begin{array}{llll} f'(x)&=\left( \frac{x^3}{x^2-3} \right)'\\ &=\frac{3x^2(x^2-3)-x^3 2x}{(x^2-3)^2}\\ &=\frac{x^4-9x^2}{(x^2-3)^2}&\text{ ...we need to factor it! }\\ &=\frac{x^2(x-3)(x+3)}{(x-\sqrt{3})^2(x+\sqrt{3})^2}. \end{array}$$ Then the critical points are the ones where either the derivative is zero, i.e., the numerator is zero: $$x=0,\ 3,\ -3;$$ or undefined, i.e., the denominator is zero: $$x=-\sqrt{3},\ \sqrt{3}.$$ At these points and at these points only the derivative may change its sign.
We now list all the factors. They are simple enough for us to determine where and whether they change their signs: $$\begin{array}{l|ccc} \text{factors }& \text{ signs }\\ \hline x^2&+&+&+&+&+&0&+&+&+&+&+\\ x-3&-&-&-&-&-&-&-&-&-&0&+\\ x+3&-&0&+&+&+&+&+&+&+&+&+\\ (x-\sqrt{3})^2&+&+&+&+&+&+&+&0&+&+&+\\ (x+\sqrt{3})^2&+&+&+&0&+&+&+&+&+&+&+\\ \text{domain }&\cdots&\bullet&\cdots&\circ&\cdots&\bullet&\cdots&\circ&\cdots&\bullet&\cdots&\to x\\ x=&&-3&&-\sqrt{3}&&0&&\sqrt{3}&&3\\ f'&+&0&-&\vdots&-&0&-&\vdots&-&0&+\\ &&\cdot&&\vdots&\searrow& &&\vdots&&&\\ f&\nearrow&&\searrow&\vdots&&\cdot&&\vdots&\searrow&&\nearrow\\ &&&&\vdots&&&\searrow&\vdots&&\cdot& \end{array}$$ Then we go vertically and determine the sign of the derivative using: $+\cdot-=-$, etc. The increasing and decreasing behavior of $f$ is then derived. The extrema are visually classified. We also detect the two vertical asymptotes.
This data is sufficient for us to plot by hand a rough sketch of the graph:
We just can't guarantee this concavity... $\square$
We can classify extreme points with the help of just the second derivative at that point.
Theorem (Second Derivative Test). Suppose $f$ is twice differentiable at $x=c$ and suppose $f'(c) = 0$. Then,
- if $f' '(c) \le 0$, then $c$ is a local max point;
- if $f' '(c) \ge 0$, then $c$ is a local min point.
Warning: If $f' '(c) = 0$, then test fails.
Example. Some possibilities:
- max/min: $ f(x) = x^{4}\ \Longrightarrow\ f' '(0) = 0. $
- neither: $ f(x) = x^{3}\ \Longrightarrow\ f' '(x) = 6x. $
$\square$
Example. Let $$f(x) = \frac{x^{2}}{x^{2} - 1}.$$
- Domain is all reals except $x = \pm 1 $.
- Vertical asymptotes: $ x = 1,\ x = -1$.
- Horizontal asymptote: $ y= 1$.
Now compute the derivatives. $$\begin{aligned} f'(x) &= \frac{2x(x^{2} - 1) - x^{2}\cdot 2x}{(x^{2} - 1)^{2}} \\ &= \frac{2x^{3} - 2x - 2x^{3}}{(x^{2} - 1)^{2}} \\ &= - \frac{2x}{(x^{2} - 1)^{2}}. \end{aligned}$$ We had to simplify in order to differentiate again. $$\begin{aligned} f' '(x) &= -\frac{2(x^{2} - 1)^{2} - 2x \cdot 2(x^{2} - 1) 2x}{(x^{2} - 1)^{4}} \\ & = - \frac{2(x^{2} - 1)(x^{2} - 1 - 4x^{2})}{(x^{2} - 1)^{4}} \\ & = \frac{2(x-1)(x+1)(3x^{2} + 1)}{(x^{2} - 1)^{4}}. \end{aligned}$$ We had to simplify in order to factor.
We now need find the signs of the factors and then the signs of the derivatives. We take note of the domain and only list the factors that may change sign. $$\begin{array}{l|ccc} \text{factors }& \text{ signs }\\ \hline -x&+&\vdots&+&0&-&\vdots&-\\ f'&+&\vdots&+&0&-&\vdots&-\\ f&\nearrow&\vdots&\nearrow&&\searrow&\vdots&\searrow\\ \hline x-1 &-&-&-&-&-&0&+\\ x+1 &-&0&+&+&+&+&+\\ f' '&+&\vdots &-&-&-&\vdots &+\\ f&\smile&\vdots&\frown&\frown&\frown&\vdots&\smile\\ \hline \text{domain }&\cdots&\circ&\cdots&\bullet&\cdots&\circ&\cdots&\to x\\ x=&&-1&&0&&1&&\\ \hline &\nearrow&\vdots&&&&\vdots&\searrow\\ f&&\vdots&&\cdot&&\vdots&\\ &&\vdots&\nearrow&\frown&\searrow&\vdots& \end{array}$$
This data is sufficient for us to plot by hand a rough sketch of the graph:
$\square$
Exercise. Solve a reversed problem: sketch the graph of $f$ with the following properties:
- $f' > 0$ on $(-\infty,0)$ and $(1,2)$.
- $f' < 0$ on $(0,1)$ and $(2,\infty)$.
- $f' ' > 0$ on $(-\infty,-1)$ and $(2,\infty)$.
- $f' ' < 0$ on $(-1,2)$.
Anti-differentiation: the derivative of what function?
Before the Mean Value Theorem, we have only been able to find facts about the derivative from the facts about the function. This is a short list of familiar facts: $$\begin{array}{l|l|ll} \text{info about }f &&\text{ info about }f'\\ \hline f\text{ is constant }&\Longrightarrow &f' \text{ is zero}\\ &\overset{?}{\Longleftarrow}&\\ \hline f\text{ is linear}&\Longrightarrow &f' \text{ is constant}\\ &\overset{?}{\Longleftarrow}&\\ \hline f\text{ is quadratic}&\Longrightarrow &f' \text{ is linear}\\ &\overset{?}{\Longleftarrow}&\\ \hline \end{array}$$ Are these arrows reversible? If the derivative of the function is zero, does it mean that the function is constant? This time, we have a tool to prove this fact. The Mean Value Theorem says that if $f$ is continuous on $[a,b]$ and differentiable on $(a,b)$, then $$\frac{f(b) – f(a)}{b-a} = f'(c),$$ for some $c$ in $(a,b).$
The theorem will help us with facts about the function derived from the facts about its derivative.
Consider this obvious statement about motion:
- “if my speed is zero, I am standing still (and vice versa)”.
If a function $y=f(x)$ represent the position, we can restate this mathematically. Proving the mathematical version of this statement will confirm that our theory matches the reality and the common sense.
Theorem (Constant). (A) A function defined at the nodes of a partition of interval $[a,b]$ has a zero difference and difference quotient for all secondary nodes in the partition if and only if this function is constant over the nodes of $[a,b]$; i.e., $$\frac{\Delta f}{\Delta x} = 0\ \Longleftrightarrow\ \Delta f=0 \ \Longleftrightarrow\ f=\text{ constant }.$$ (B) A differentiable on open interval $I$ function has a zero derivative for all $x$ in $I$ if and only if this function is constant on $I$; i.e., $$f'=0 \ \Longleftrightarrow\ f=\text{ constant }.$$
Proof. (A) $$\frac{\Delta f}{\Delta x}(c_i) = 0 \ \Longrightarrow\ f(x_{i})-f(x_{i-1})=0\ \Longrightarrow\ f(x_{i})=f(x_{i-1}).$$ (B) To prove that $f$ is constant, it suffices to show that $$f(a) = f(b),$$ for all $a,b$ in $I$. Assume $a < b$ and use the Mean Value Theorem with interval $(a,b)$ inside the interval $I$: $$\frac{f(b) – f(a)}{b-a} =f'(c),$$ for some $c$ $(a,b)$. This is $0$ by assumption. Therefore, we have: $$\frac{f(b) - f(a)}{b-a} = 0,$$ for all pairs $a,b$. Hence $$f(b) – f(a) = 0,$$ or $$f(a) = f(b).$$ $\blacksquare$
The converse was proven in Chapter 8.
Note that the proof of the Monotonicity Theorem is identical to the one above with each “$=$” replaced with “$>$”.
Exercise. What if $f'=0$ on a union of two intervals?
Suppose now that there are two runners running with the same speed; what can we say about their mutual locations? They are not, of course, standing still, but they are still relative to each other! We have a slightly less obvious fact about motion:
- “if two runners run with the same speed, the distance between them isn't changing (and vice versa)”.
It's as if they are holding the two ends of a pole without pulling or pushing.
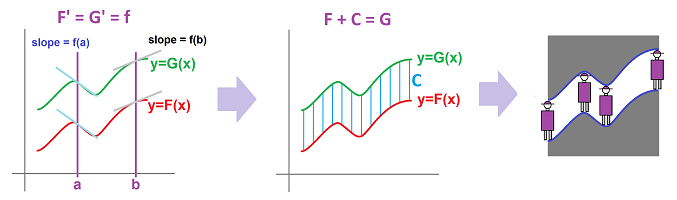
The fact remains valid even if they speed up and slow down all the time. Once again, for functions $y=F(x)$ and $y=G(x)$ representing their position, we can restate this idea mathematically in order to confirm that our theory makes sense.
Theorem (Anti-differentiation). (A) Two functions defined at the nodes of a partition of interval $[a,b]$ have the same difference quotient if and only if differ by a constant; i.e., $$\frac{\Delta F}{\Delta x}(c) = \frac{\Delta G}{\Delta x}(c) \ \Longleftrightarrow\ \Delta F(c) = \Delta G(c) \ \Longleftrightarrow\ F(x) – G(x)=\text{ constant }.$$ (B) Two differentiable on open interval $I$ functions have the same derivative if and only if differ by a constant; i.e., $$F'(x) = G'(x) \ \Longleftrightarrow\ F(x) – G(x)=\text{ constant }.$$
Proof. Define $$h(x) = F(x) – G(x).$$ Then, by SR, we have: $$h'(x) = \left( F(x)–G(x) \right)'=F'(x)–G'(x) =0,$$ for all $x$. Then $h$ is constant, by the Constant Theorem. $\blacksquare$
The converse was proven in Chapter 8.
Geometrically, the theorem says:
- if the graphs of $y=F(x)$ and $y=G(x)$ have parallel tangent lines for every value of $x$, then the graph of $F$ is a vertical shift of the graph of $G$ (and vice versa).
We can understand this idea if we imagine a tunnel with the slope of its top equal to the slope of the bottom at every location. Then the height of the tunnel remains the same throughout its length.
In fact, we have infinitely many -- one for each $C$ -- solutions to the problem $F'=f$:
So, even if we can recover the function $F$ from it derivative $F'$, there many others with the same derivative, such as $G=F+C$ for any constant real number $C$. Are there others? No, according to the theorem.
Warning: it's only true when the domain is an interval.
Based on the theorem, we can now update this list of simple but important facts: $$\begin{array}{l|l|ll} \text{info about }f &&\text{ info about }f'\\ \hline f\text{ is constant }&\Longleftrightarrow &f' \text{ is zero}\\ f\text{ is linear}&\Longleftrightarrow &f' \text{ is constant}\\ f\text{ is quadratic}&\Longleftrightarrow &f' \text{ is linear}\\ \hline \end{array}$$ In fact, $f$ is a polynomial of degree $n$ is and only if $f'$ is a polynomial of degree $n-1$.
Antiderivatives
Definition. (A) Suppose a function $f$ is defined on the secondary nodes of a partition of a closed interval $I$. Then a function $F$ defined on the nodes of the partition that satisfies $\frac{\Delta F}{\Delta x}(c) = f(c)$ for all $c$ is called an antiderivative of $f$. (B) Suppose a function $f$ is defined on an open interval $I$. Then a function $F$ defined on $I$ that satisfies $\frac{dF}{dx}(x) = f(x)$ for all $x$ is called an antiderivative of $f$.
We use “an” because there are many antiderivatives for each function. As we know from the Anti-differentiation Theorem, if $F$ is an antiderivative of $f$ then so is $F+C$, where $C$ is any constant, while the converse is only for functions defined on intervals.
We can think of the definition as an equation, an equation for functions: $$\begin{array}{|l|}\hline\quad \text{Given } f, \text{ solve for } F:\\ \frac{\Delta F}{\Delta x} = f, \text{ or } \frac{dF}{dx}=f.\quad \\ \hline\end{array}$$ For example, the task may be: find all $F$ that satisfy the equation: $$F'=x^2.$$ It's not surprising that an equation has many solutions (just like $x^2=1$). We can restate the Anti-differentiation Theorem as follows.
Corollary. Suppose a function $f$ is defined on an open interval $I$ and $F$ is one of its antiderivatives. Then the set of all antiderivatives is $$\{F+C:\ C \text{ real }\}.$$
It is the solution set of the equation and it may be called the antiderivative.
Exercise. Suppose a function $f$ is defined on an open interval $I$. Prove that (a) the graphs of two different antiderivative of $f$ never intersect; (b) for every point $(x,y)$ with $x$ within $I$, there is an antiderivative of $f$ the graph of which passes through it.
The problem then becomes the one of finding a single function $F$, either
- from its difference quotient $\frac{\Delta F}{\Delta x}$, or
- from its derivative $\frac{dF}{dx}$.
In other words, we reconstruct the function from a “field of slopes”:
One can imagine a flow of liquid with the direction known at every location. How do we find the path of a particular particle? The process of reconstructing a function, $F$, from its derivative, $f$, is called anti-differentiation.
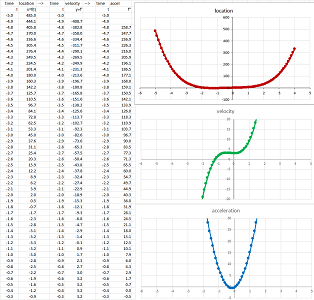
The anti-differentiation problem has been solved on several occasions for the former, discrete case -- velocity from acceleration and location from velocity -- via these recursive formulas (a series): $$F(x_{n+1})=F(x_n)+f(c_n)\Delta x_n.$$ For each location, we look up the velocity, find the next location, and repeat:
If the nodes of the partition are close enough to each other, these points form curves:
For the latter, continuous case, this is a challenging problem: how does one plot a curve that follows these -- infinitely many -- tangents?
To begin with, we just try to reverse differentiation. We will try to construct a theory of anti-differentiation that matches -- as much as possible -- that of differentiation.
Here is a short list of derivatives of functions (for all $x$ for which the function is differentiable): $$\begin{array}{|rcll|} \hline \text{function} & \longrightarrow & \text{derivative} \\ \hline x^{r} & & rx^{r-1} \\ \ln x & & \frac{1}{x} \\ e^{x} & & e^{x} \\ \sin x & & \cos x \\ \cos x & & -\sin x\\ \hline \text{antiderivative} & \longleftarrow & \text{function}\\ \hline \end{array}$$ To find antiderivatives, reverse the order: read each line from right to left!
It is that simple! We just may need some tweaking to make the formulas as easy to apply as the original.
For example, let's find antiderivatives of $x^{n}$. Use the Power Formula for differentiation (the first row), divide by $r$, and apply CMR: $$(x^{r})' = rx^{r-1}\ \Longrightarrow\ \frac{1}{r}(x^{r})' = x^{r-1}\ \Longrightarrow\ \left(\frac{1}{r} x^{r}\right)' = x^{r-1}. $$ We then simplify the right-hand side by setting $r-1 = s$: $$\left( \frac{1}{s + 1}x^{s + 1} \right)' = x^{s}. $$ The right-hand side become the left-hand side and we have the Power Formula for anti-differentiation:
- an antiderivative of $x^{s}$ is $\frac{1}{s + 1}x^{s + 1}$, provided $s \neq -1$.
What if $s = -1$? Then we read the answer from the next line in the table:
- an antiderivative of $x^{-1}$ is $\ln |x|$.
Note that the rule “the derivative of the power function is a power function of degree $1$ lower” has an exception, the $0$-power, and the rule “the antiderivative of the power function is a power function of degree $1$ higher” has an exception too.
Taking the rest of these rows, we have a list of antiderivatives of functions, on open intervals: $$\begin{array}{|rcll|} \hline \text{function} & \longrightarrow & \text{antiderivative} \\ \hline x^{s}&& \frac{1}{s + 1} x^{s + 1}, \quad s \neq -1 \\ \frac{1}{x}&& \ln |x|\\ e^{x} && e^{x}\\ \sin x && -\cos x \\ \cos x &&\sin x\\ \hline \text{derivative} & \longleftarrow & \text{function}\\ \hline \end{array}$$
Warning: each formula is only valid on open interval on which the antiderivative is defined, but the only item that matters though is this:
- $\ln (x)$ is an antiderivative of $\frac{1}{x}$ on the interval $(0,+\infty)$, and
- $\ln (-x)$ is an antiderivative of $\frac{1}{x}$ on the interval $(-\infty,0)$.
Next, we will need the rules of anti-differentiation.
First, consider Sum Rule for derivatives: $$(f + g)' = f' + g'.$$ Let's read it from right to left.
Theorem (Sum Rule). An anti-derivative of the sum is the sum of antiderivatives; i.e., if
- $F$ is an antiderivative of $f$ and
- $G$ is an antiderivative of $g$,
then
- $F+G$ is an antiderivative of $f+g$.
Proof. We apply SR: $$\left( F(x)+G(x) \right)'= F'(x)+G'(x)=f(x)+g(x).$$ $\blacksquare$
Exercise. What about the converse?
Similarly, we acquire the following.
Theorem (Constant Multiple Rule). An anti-derivative of a multiple is the multiple of an antiderivative; i.e., if
- $F$ is and antiderivative of $f$ and
- $c$ is a constant,
then
- $cF$ is an antiderivative of $cf$.
Proof. We apply CMR: $$\left( cF(x) \right)'= cF'(x)=cf(x).$$ $\blacksquare$
Exercise. What about the converse?
Example. With these rules, anti-differentiation is very similar to differentiation. Find an antiderivative of $$3x^{2} + 5e^{2} + \cos x.$$ We simply find antiderivatives of each term: $$ 3\cdot \frac{x^{3}}{3} + 5e^{x} + \sin x. $$ Just as when solving equations, we can easily confirm that our computations were correct, by substitution. In this case, we differentiate the antiderivative: $$\begin{aligned} (x^{3} + 5e^{x} + \sin x)' &= (x^{3})' + 5(e^{x})' + (\sin x)' \\ &= 3x^{2} + 5e^{x} + \cos x. \end{aligned}$$ This is the original function! The answer checks out. $\square$
We can handle compositions just as easily but only when one of the function is linear.
Theorem (Linear Composition Rule). If
- $F$ is an antiderivative of $f$ and
- $a\ne 0,\ b$ are constants,
then
- $\tfrac{1}{a}F(ax+b)$ is an antiderivative of $f(ax+b)$.
Proof. We apply CMR and CR: $$\left( \tfrac{1}{a}F(ax+b) \right)'=\tfrac{1}{a} \left( F(ax+b) \right)'=\tfrac{1}{a} a F'(ax+b)=F'(ax+b)=f(ax+b).$$ $\blacksquare$
Below is the standard notation for the antiderivative of a function $f$: $$\int f\, dx.$$ Here $\int$ is called the integral sign. It looks like a stretched letter “S”, which stands for “summation”:
This is how the notation is deconstructed: $$\begin{array}{lrrrl} \text{a specific function}&&&\text{a specific function}\\ \qquad\downarrow&&&\downarrow\qquad\qquad\\ \int \big(\quad 3x^{2} & + \cos x \quad\big)dx &=&x^{3} + \sin x+C\\ \uparrow&\uparrow&&\uparrow\\ \text{left and}&\text{right parentheses}&&\text{ indicates that there are others} \end{array}$$ This is how we re-write the above list: $$\begin{array}{rll} \int x^{s}\, dx&= \frac{1}{s + 1} x^{s + 1}+C, \quad \text{ for }s \neq -1;\\ \int \frac{1}{x}\, dx&= \ln x+C, \ x > 0 \text{ or } x<0;\\ \int e^{x}\, dx&= e^{x}+C;\\ \int \sin x\, dx&= -\cos x +C;\\ \int \cos x\, dx&=\sin x+C. \end{array}$$
We restate the rules too.
Sum Rule: $$\int (f+g)dx=\int f\, dx+\int g\, dx.$$
Constant Multiple Rule: $$\int (cf)dx=c\int f\, dx.$$
Linear Composition Rule: $$\int f(mx+b)dx=\tfrac{1}{m}\int f(t)\, dt\Big|_{t=mx+b}.$$
Below, we have these two diagrams to illustrate the interaction of antiderivatives with algebra: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{ccc} f,g&\la{\int}&f',g'\\ \ \da{+}& &\ \da{+}\\ f+g & \la{\int}&f'+g' \end{array}\qquad \begin{array}{ccc} f&\la{\int}&f'\\ \ \da{\cdot c}& &\ \da{\cdot c}\\ cf & \la{\int}&cf' \end{array}$$ The arrows of differentiation are reversed! We start with a pair of functions at top right, then we proceed in two ways:
- left: anti-differentiate them, then down: add the results; or
- down: add them, then left: anti-differentiate the results.
The result is the same!
So far, this is very similar to differentiation. Unfortunately, there is no easy way to express an antiderivative of a product of two functions in terms of their antiderivatives! There is no Product Rule for anti-differentiation, nor Quotient Rule, nor Chain Rule. Most of the time, this is best we can do:
- Problem: Find an antiderivative of $x\cdot e^{x}$. No rule...
- Problem: Find an antiderivative of $2x\cdot e^{x^{2}}$. From our prior experience, we simply recognize this as an outcome of differentiation:
$$ (e^{x^{2}})' = 2x\cdot e^{x^{2}}. $$
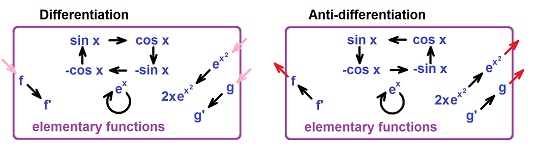
This difference has profound consequences. We can start with just these three functions: $$x^s,\ \sin x, e^x.$$ Then -- by applying the four algebraic operations, composition, and inverting -- we can construct a great variety of functions. Let's call them “elementary functions”. Because of the way they are constructed, all of them can be easily differentiated with the rules of differentiation. Contrary to what the above list might suggest, anti-differentiation will often take us outside of the realm of elementary functions. For example, a new function, called the Gauss error function, must be created for this important antiderivative: $$\operatorname{erf}(x)=\frac{2}{\sqrt{\pi}}\int e^{-x^2}\, dx.$$
The result will be the same if we exclude from the “elementary functions” either the trigonometric functions or the exponent. It is also a known fact that adding more functions to the list won't resolve the issue.
With the help of the Anti-differentiation Theorem, we can claim that we have found all antiderivatives of these functions on our list, over open intervals within the domains of antiderivatives, i.e., the antiderivative of the corresponding function.
Definition. For a given function $f$, the general antiderivative of $f$ over open interval $I$ is defined by: $$\int f \, dx=F(x) +C,$$ where $F$ is any antiderivative of $f$ on $I$, i.e., $F'=f$, understood as a collection of all such functions over all possible real numbers $C$. This collection is also called the indefinite integral of $f$.
These diagrams illustrate how differentiation and anti-differentiation undo each other: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccc} f & \mapsto & \begin{array}{|c|}\hline\quad \int\square\, dx \quad \\ \hline\end{array} & \mapsto & F & \mapsto &\begin{array}{|c|}\hline\quad \tfrac{d}{dx}\square \quad \\ \hline\end{array} & \mapsto & f;\\ F & \mapsto & \begin{array}{|c|}\hline\quad \tfrac{d}{dx}\square \quad \\ \hline\end{array} & \mapsto & f & \mapsto &\begin{array}{|c|}\hline\quad \int\square\, dx \quad \\ \hline\end{array} & \mapsto & F+C. \end{array}$$ In the second row, we see that $\tfrac{d}{dx}$ isn't invertible.
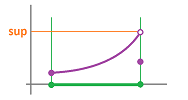
Example. There are infinitely many antiderivatives but there is more to it. Let's take a more careful look at one line on the list: $$\int \frac{1}{x}\, dx \overset{?}{=} \ln |x|+C, \quad x \neq 0.$$ This formula is intended to mean that
- 1. we have captured infinitely many -- one for each real number $C$ -- antiderivatives, and
- 2. we have captured all of them.
However, the Anti-differentiation Theorem applies only to one interval at a time. Meanwhile, the domain of $1/x$ consists of two rays $(-\infty, 0)$ and $(0, +\infty)$. As a result, we solve this problem separately on either of the two intervals. Then the antiderivatives of $1/x$ are:
- $\ln(-x)+C$ on $(-\infty, 0)$, and
- $\ln(x)+C$ on $(0, +\infty)$.
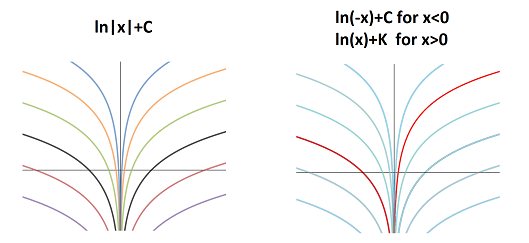
But if now we were to combine each of these pairs of functions into one, $F$, defined on $(-\infty, 0)\cup (0, +\infty)$, we would realize that, every time, the two constants might be different: after all, they have nothing to do with each other! We illustrate the wrong (incomplete) answer on the left and the right one on the right:
The image on the left, as well as the formula we started with, might suggest that all of the function's antiderivatives are even functions. The image on the right shows a single antiderivative (in red) but its two branches don't have to match! Algebraically, the antiderivative of $\frac{1}{x}$ -- on the whole domain -- is given by this piece-wise defined function: $$F(x)= \begin{cases} \ln(-x)+C & \text{ for } x \in (-\infty, 0), \\ \ln(x)+K & \text{ for } x \in (0, +\infty). \end{cases}$$ It has two parameters instead of the usual one. $\square$
Exercise. Verify that this is an antiderivative of $1/x$.
Exercise. In a similar fashion, examine the Power Formula above for $s<-1$.
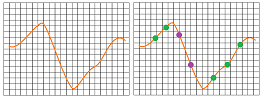
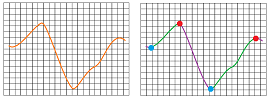
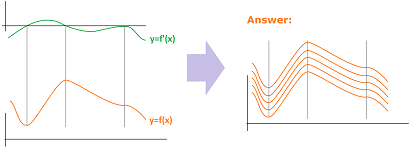
Example. The antiderivatives on our list were discovered by reading the results of differentiation backwards. We can do the same for graphs. Below, the derivative's graph (green) was found from the graph of the function (red) by looking at the monotonic behavior of $f$: either $f'>0$ or $f'<0$ and local extreme points: $f'=0$.
In reverse, we may see how things are discovered by reading the diagram upward: from green to red. We look at the intervals where $f'$ keeps the same sign and discover the intervals where $f\searrow$ or $f\nearrow$, as well as the intervals where $f'$ changes its sign and discover the max or min of $f$. Here is another example how the graph of $f$ is found from the graph of its derivative:
An additional feature here is an inflection point. We also make sure that a multitude of antiderivatives is shown. $\square$
This study continues in Chapter 11.
The limit of the difference quotient is the derivative
This section can be omitted on the first reading.
The derivative is defined as the limit of the difference quotient; now we also have a back link. Indeed, what if we take the partition of $[a,b]$ to trivial: $n=1,\ x_0=a,\ x_1=b$? The Mean Value Theorem simply states that the two are equal, provided we choose the right point where to sample the derivative. For an arbitrary partition, we carry out the construction for each interval of the partition, as follows.
Corollary. Suppose
- 1. $f$ is continuous on $[a,b]$,
- 2. $f$ is differentiable on $(a,b)$.
Then for any partition of the interval $[a,b]$, there are such secondary nodes $c_1,...,c_n$ that $$\frac{\Delta f}{\Delta x}(c_k)=f'(c_k), \ k=1,2,...,n.$$
In other words, the slopes of the lines connecting the points of the graph of $f$ at the nodes of the partition are equal to the values of the derivative at the secondary nodes between them:
Therefore, the difference quotient provides a sampling of the derivative. With finer and finer partitions, we will have denser and denser samplings of the derivative. That is why the graph of the derivative is approximated so well by the graph -- nothing but disconnected dots -- of the difference quotient:
We defined the derivative as the limit of the difference quotient -- but only one point a time!
By definition, we have: $$f'(c) =\lim_{h\to 0} \frac{f(c+h)-f(c)}{h}.$$ In other words, for every $\varepsilon >0$ there is a $\delta >0$ such that for any positive $h$ with $h<\delta$, we have : $$\left| f'(c) - \frac{f(c+h)-f(c)}{h} \right|<\varepsilon.$$ We discover, in fact, that the whole difference quotient, a function, converges to the derivative!
Theorem. Suppose $f$ is continuously differentiable on an open interval containing $[a,b]$. Then, for every $\varepsilon >0$ there is a $\delta >0$ such that for any partition of $[a,b]$ with $\Delta x_i<\delta$ for all $i$, we have at any secondary node $c_k$: $$\left| f'(c_k) - \frac{\Delta f}{\Delta x_k}(c_k) \right|<\varepsilon.$$
Proof. The Mean Value Theorem allows us to choose $c_k$ and the definition of the derivative stated above guarantees that there is $\delta$ for each $\varepsilon$. But why is this the same $\delta$ for all $k$? We will provide the proof later.
$\blacksquare$
Exercise. Describe how the theorem applies to the picture that precedes it.
We also use the Mean Value Theorem to provide a new version of the theorem: halfway between discrete and continuous.
Theorem (Chain Rule). The difference quotient of the composition of two functions is found as the product of the difference quotient and the derivative. (AB) For any function $x=f(t)$ defined at two adjacent nodes $t$ and $t+\Delta t$ of a partition and any function $y=g(x)$ differentiable on an open interval containing $f(t)$ and $f(t+\Delta t)$, there is such a $q$ between $x$ and $u$ that we have the difference quotients (defined at a secondary node $c$ in $[t,t+\Delta t]$) and the derivative (defined at $q$) satisfy: $$\frac{\Delta (g\circ f)}{\Delta t}(c)= \frac{dg}{dx}(q) \cdot \frac{\Delta f}{\Delta t}(c).$$ Furthermore, if $f$ is defined and continuous on the interval $[t,t+\Delta t]$, the value of $c$ can be chosen in such a way that $f(c)=q$. (BA) For any function $x=f(t)$ differentiable inside an interval $[t,t+\Delta t]$ with $\Delta t\ne 0$ and continuous on the whole interval and for any function $y=g(x)$ defined at two adjacent nodes $x=f(t)$ and $x+\Delta x=f(t+\Delta t)$ of a partition, there is such a choice of a secondary node $c$ in the interval $[t,t+\Delta t]$ that we have the derivative (defined at $c$) and the difference quotients (defined at $c$ and $q$) satisfy: $$\frac{\Delta (g\circ f)}{\Delta t}(c)= \frac{\Delta g}{\Delta x}(q)\cdot\frac{df}{dt}(c).$$
Proof. (AB) Let $$x=f(t) \text{ and } u=f(t+\Delta t).$$ In the proof presented in Chapter 8 we assumed that $x \ne u$. Not anymore! Indeed, if $x=u$, we have: $$\frac{\Delta f}{\Delta t}(c)=\frac{f(t+\Delta t)-f(t)}{\Delta t}=\frac{0}{\Delta t}=0,$$ so, the right-hand side of the identity is $0$. Similarly, in the left-hand-side, we have: $$\frac{\Delta (g\circ f)}{\Delta t}(c)=\frac{(g\circ f)(t+\Delta t)-(g\circ f)(t)}{\Delta t}=\frac{g( f(t+\Delta t)-g(f(t))}{\Delta t}=\frac{0}{\Delta t}=0,$$ and the identity holds. When $x\ne u$, we, just as before, apply the Mean Value Theorem. There is $q$ between $x$ and $u$ such that: $$\frac{g(u)-g(x)}{u-x}=g'(q).$$ Then: $$\begin{array}{lll} \frac{\Delta (g\circ f)}{\Delta t}(c)&=\frac{(g\circ f)(t+\Delta t)-(g\circ f)(t)}{\Delta t}\\ &=\frac{g(f(t+\Delta t))-g(f(t))}{f(t+\Delta t)-f(t)}\cdot \frac{f(t+\Delta t)-f(t)}{\Delta t}\\ &=\frac{g(u)-g(x)}{u-x}\cdot \frac{f(t+\Delta t)-f(t)}{\Delta t}\\ &=g'(q) \cdot \frac{\Delta f}{\Delta t}(c). \end{array}$$ Finally, if $f$ is defined and continuous on the interval $[t,t+\Delta t]$, the value of $c$ can be chosen in such a way that $f(c)=q$, by the Intermediate Value Theorem.
(BA) First, by the Mean Value Theorem there is $c$ in the interval $[t,t+\Delta t]$ such that: $$\frac{f(t+\Delta t)-f(t)}{\Delta t}=f'(c).$$ Then: $$\begin{array}{lll} \frac{\Delta (g\circ f)}{\Delta t}(c)&=\frac{(g\circ f)(t+\Delta t)-(g\circ f)(t)}{\Delta t}\\ &=\frac{g(f(t+\Delta t))-g(f(t))}{f(t+\Delta t)-f(t)}\cdot \frac{f(t+\Delta t)-f(t)}{\Delta t}\\ &=\frac{g(x+\Delta x)-g(x)}{\Delta x}\cdot \frac{f(t+\Delta t)-f(t)}{\Delta t}\\ &=\frac{\Delta g}{\Delta x}(q)\cdot f'(c). \end{array}$$ $\blacksquare$
The continuous version of the Chain Rule, $$\frac{d(g\circ f)}{dt}(c)= \frac{dg}{dx}(f(c))\cdot\frac{df}{dt}(c).$$ follows from the two last theorems (under the condition of continuous differentiability on an open interval).
The concepts will continue to develop following this idea: $$\lim_{\Delta x\to 0}\left( \begin{array}{cc}\text{ discrete }\\ \text{ calculus }\end{array} \right)= \text{ calculus }.$$