Calculus I -- Fall 2016 -- final

MATH 229 -- Fall 2016 -- final exam

Name:_________________________ $\qquad$ 10 problems, 100 points total

• Write the problems in the given order, each problem on a separate page.
• Show enough work to justify your answers.

$\bullet$ 1. Find the domains of the functions: (a) $\frac{x+1}{\sqrt{x^2-1}}$; (b) $\sqrt[4]{x+1}$.

$\bullet$ 2. Sketch the graph of the function $f(x)=x^{4}-x^2$. Provide justification for each feature of the graph.

$\bullet$ 3. Calculate the derivative of $f(x) = x^{\pi} + \pi^{x} + x + \pi$ indicating the rules you use.

$\bullet$ 4. Suppose $f'(1)=2$, $g'(2)=3$, and $h'(1)=6$, where $h=g\circ f$. What is $f(1)$?

$\bullet$ 5. Find an equation of the line tangent to the curve $x^{2}+y^{2}=x$ passing through the point $(0,0)$.

$\bullet$ 6. Set up but do not solve the optimization problem for the following situation: “Among all right triangles with area $10$, find the one with the smallest perimeter”.

$\bullet$ 7. Find the point on the line $y=\pi$ that is closest to the origin.

$\bullet$ 8. (a) State the Fundamental Theorem of Calculus. (b) Use part (a) to evaluate $\int_{0}^1 \sin \frac{x}{3} \, dx$.

$\bullet$ 9. Evaluate (a) $\int (3x)^2\, dx$; (b) $\int e^{x^2}2x\, dx$.

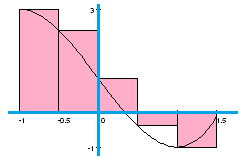
$\bullet$ 10. Evaluate the Riemann sum of $f$ below on the interval $[-1,1.5]$ with $n=5$. What are its sample points? What does it estimate?