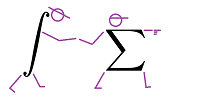This site is being phased out.
The integral
Contents
- 1 The Area Problem
- 2 The total value of a function: the Riemann sum
- 3 The Fundamental Theorem of Calculus
- 4 How to approximate areas and displacements
- 5 The limit of the Riemann sums: the Riemann integral
- 6 Properties of the Riemann sums and the Riemann integrals
- 7 The Fundamental Theorem of Calculus, continued
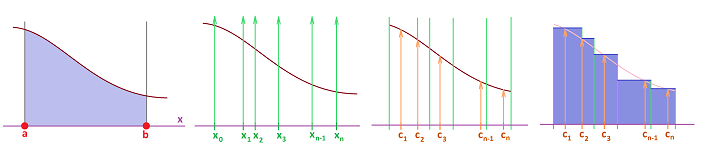
The Area Problem
We know that the area of a circle of radius $r$ is supposed to be $A = \pi r^{2}$.
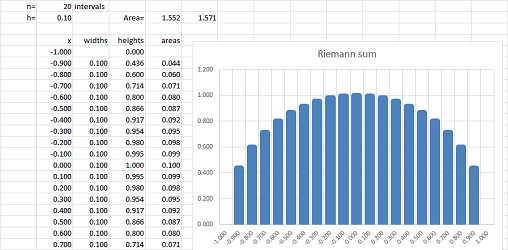
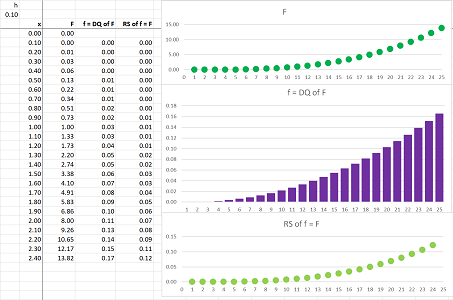
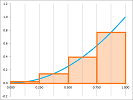
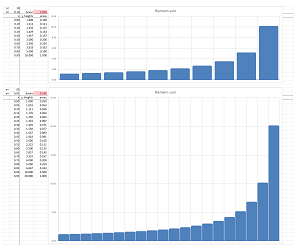
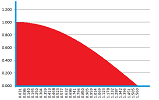
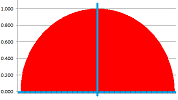
Example. Let's review what we accomplished in Chapter 1. We confirm the formula with nothing but a spreadsheet. We plot the graph of the function: $$f(x)=\sqrt{1-x^2},\ -1\le x\le 1,$$ and then cover this half-circle with vertical bars based on the interval $[-1,1]$:
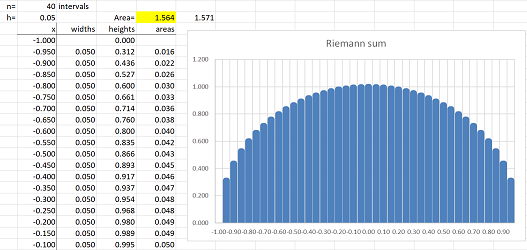
Then the area of the circle is approximated by the sum of the areas of the bars! In the spreadsheet, a column of the widths of the bars are multiplied by the heights and then the result is placed in the last column. Finally, we add all entries in this column. The result is $$\text{Approximate area of the semicircle}= 1.552.$$ It is close to the theoretical result obtained later in this chapter: $$\text{Exact area of the semicircle}= \pi/2=1.571.$$ What is new? Following the approach presented in Chapter 7, we improve our approximation by making the intervals smaller and smaller. Redoing the computation with $40$ intervals gives a better approximation, $1.564$:
Nothing stops us from improving this approximation further and further! $\square$
Exercise. Approximate the area of the circle of radius $1$ within $.0001$.
We have showed that indeed the area of the circle is close to what's expected. But the real question is: what is the area? Do we even understand what it is?
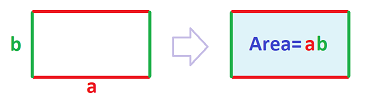
One thing we do know. The area of a rectangle $a \times b$ is $a b$.
Furthermore, any right triangle is simply a half of a diagonally cut rectangle:
We can also cut any triangle into a pair of right triangles:
Finally, any polygon can be cut into triangles:
So, we can find -- and we understand -- the areas of all polygons. They are geometric objects with straight edges.
But what are the areas of curved objects?
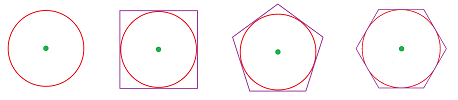
Example (circle). Let's review the ancient Greek's approach to understanding and computing the area (and the length) of a circle. They approximated the circle with regular polygons: equal sides and angles. We put such polygons around the circle so that it touches them from the inside (“circumscribing” polygons):
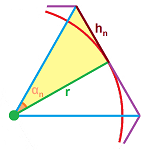
For each $n=3,4,5,...$, the following is carried out. We split each such polygon with $n$ sides into $2n$ right triangles and compute their dimensions:
Each of them has the angle at the center that is one $2n$th of the whole: $$\alpha_n=\frac{2\pi}{2n}=\frac{\pi}{n}.$$ The side that touches the circle is its radius and the opposite side is $r\tan \tfrac{\pi}{n}$. Therefore, the area of the triangle is $$a_n=\frac{1}{2}\cdot r \cdot r\tan \tfrac{\pi}{n}=\frac{r^2}{2}\tan \tfrac{\pi}{n}.$$ We know now the area of the whole polygon, $$A_n=a_n\cdot 2n=\frac{r^2}{2}\tan \tfrac{\pi}{n}\cdot 2n,$$ and can examine the data: $$\begin{array}{l|ll} n&3 &4 &5 &6 &7 &8 &9 &10 &11 &12 &13 &14 &15\\ \hline A_n&5.196 &4.000 &3.633 &3.464 &3.371 &3.314 &3.276 &3.249 &3.230 &3.215 &3.204 &3.195 &3.188 \end{array}$$ This confirms the answer one more time... On to the next level, let's compute the limit of these areas: $$\begin{array}{lll} A_n&=\frac{r^2}{2}\tan \tfrac{\pi}{n}\cdot 2n &\text{ ...we rearrange the terms in order to use...}\\ &=\pi r^2\cdot\frac{\sin \frac{\pi}{n}}{\tfrac{\pi}{n}}\cdot\frac{1}{\cos\tfrac{\pi}{n}}&\text{...one of the famous limits from Chapter 5,}\\ &\to \pi r^2 & \text{ as }n\to\infty.\end{array}$$ In order to fully justify the result, the Greeks also put such polygons around the circle so that it touches them from the outside (“inscribing” polygons). $\square$
Exercise. Carry out this construction for the inscribed polygons.
Let's compare these two seemingly unrelated problems and how they are solved: $$\begin{array}{r|l} \text{The Tangent Problem }&\text{The Area Problem}\quad\quad\\ \hline \quad \end{array}$$
Geometry. For a given curve, find the following: $$\begin{array}{r|l} \quad\\ \text{the line touching the curve at a point }&\text{ the area enclosed by the curve }\ \ \quad\quad\\ \quad \end{array}$$ The problems are easy when the curves aren't curved and, furthermore, we have solved these problems for a specific curve: the circle... The further progress depends on the development of algebra, the Cartesian coordinate system, and the idea of function (Chapters 2, 3, and 4).
Motion. The two problems are interpreted as follows: $$\begin{array}{l|r} \quad\\ \text{The slope of the tangent }&\text{ The area under the graph}\ \quad\quad\\ \text{to the position function }&\text{ of the velocity function}\ \quad\quad\\ \text{is the velocity at that moment. }&\text{ is the displacement.}\ \quad\quad\\ \quad \end{array}$$
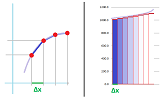
The further development utilizes dividing the domain of the function into smaller pieces, $\Delta x$ long, sampling the function, and approximating the function by means of straight lines.
Calculus. The limits of these approximations, as $\Delta x \to 0$, are the following: $$\begin{array}{r|l} \quad\\ \text{the derivative }&\text{ the integral}\quad\\ \hline \end{array}$$
We will now pursue the plan for the latter problem outlines in the right column.
The total value of a function: the Riemann sum
Example. Consider again the example of a broken odometer from the introduction. We plot the speed as a function of time:
Then we use the same formula: $$\text{ displacement }=\text{ velocity }\cdot \text{ time },$$ for each time period. Then, we add these numbers one by one to get the estimated total displacement $D$ at each moment of time. Geometrically, this means stacking these rectangles on top of each other:
$\square$
Warning: even though we often say that each such term is the “area” of the rectangle, this quantity is truly the area only if the unit of both the $x$- and the $y$-axes is that of length.
In general, we consider functions with values spread over intervals of variable lengths.
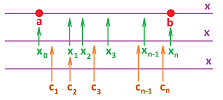
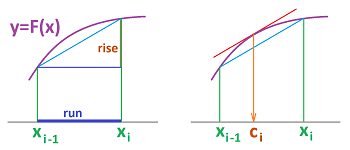
Suppose we have an augmented partition $P$ of an interval $[a,b]$ (introduced in Chapter 7).
First, we have a partition of $[a,b]$ into $n$ intervals of possibly different lengths: $$ [x_{0},x_{1}],\ [x_{1},x_{2}],\ ... ,\ [x_{n-1},x_{n}],$$ with $x_0=a,\ x_n=b$. The points $$x_{0},\ x_{1},\ x_{2},\ ... ,\ x_{n-1},\ x_{n},$$ are the primary nodes, or simply the nodes, of the partition. The lengths of the intervals are: $$\Delta x_i = x_i-x_{i-1},\ i=1,2,...,n.$$ We are also given the secondary nodes, or sample points, of $P$: $$ c_{1} \text{ in } [x_{0},x_{1}], \ c_{2} \text{ in } [x_{1},x_{2}],\ ... ,\ c_{n} \text{ in } [x_{n-1},x_{n}].$$
Definition. The Riemann sum of a function $f$ defined at the secondary nodes of an augmented partition $P$ of an interval $[a,b]$ is defined to be the following sum: $$f(c_{1})\, \Delta x_1 + f(c_{2}) \, \Delta x_2 + ... + f(c_{n})\, \Delta x_n. $$
Thus, the Riemann sum is the total “area” of the rectangles, $i=1,2,...,n$, with
- bases $[x_i,x_{i+1}]$; and
- heights $[0,f(c_i)]$.
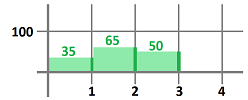
Let's consider some specific examples of Riemann sums. We assume that the lengths of the intervals are equal: $\Delta x_i=\Delta x=(b-a)/n$.
Example. Let $f(x)=x^2$ over the interval $[0,1]$ with $n=4$. Then $\Delta x =1/4$ and the interval is subdivided as before and we have five values of the function to work with: $$\begin{array}{r|cccccc} &\bullet&--&|&--&|&--&|&--&\bullet\\ x&0&&1/4&&1/2&&3/4&&1\\ x^2&0&&1/16&&1/4&&9/16&&1\\ \hline \text{left-end:}&0\cdot 1/4&+&1/16\cdot 1/4&+&1/4\cdot 1/4&+&9/16\cdot 1/4&& &\approx 0.22\\ \text{right-end:}&&&1/16\cdot 1/4&+&1/4\cdot 1/4&+&9/16\cdot 1/4&+&1\cdot 1/4&\approx 0.47. \end{array}$$ The simplest choices for the secondary nodes are the left-end or the right-end points of the intervals. We have two different Riemann sums:
$\square$
The table shows the $n$th left-end Riemann sum and the $n$th right-end Riemann sum of a function $f$ on $[a,b]$: $$\begin{array}{r|lcccccccr|} i&0&&1&&...&&n-1&&n\\ \hline [x_i,x_{i+1}]&|&--&|&-&...&-&|&--&|\\ x_i&a&&a+\, \Delta x &&...&&a+(n-1)\, \Delta x &&b\\ f(x)&f(x_0)&&f(x_1)&&...&&f(x_{n-1})&&f(x_n)\\ \text{ left-end }&f(x_0)\cdot \, \Delta x &+&f(x_1)\cdot \, \Delta x &+&...&+&f(x_{n-1}) \cdot \, \Delta x && &&\\ \text{ right-end }&&&f(x_1)\cdot \, \Delta x &+&...&+&f(x_{n-1})\cdot \, \Delta x &+&f(x_{n})\cdot \, \Delta x && \end{array}$$ The formula for such a sequence of secondary nodes is the same for both: $$c_i=a+i\, \Delta x ,$$ but the indices run over different sets:
- $i=0,1,2,...,n-1$ for the left-end points;
- $i=1,2,...,n$ for the right-end points.
The secondary nodes can also be chosen to be the mid-points of the intervals: $$\begin{array}{r|lcccccccccccr|} i&0&&1&&2&&...&&&n-1&&n\\ \hline [x_i,x_{i+1}]&|&-\cdot -&|&-\cdot -&|&-&...&&-&|&-\cdot -&|\\ c_i&&a+\tfrac{1}{2}\, \Delta x &&a+\tfrac{3}{2}\, \Delta x &&&...&&&&a+\tfrac{2n-1}{2}\, \Delta x &\\ f(x)&&f(c_0)&&f(c_1)&&&...&&&&f(c_n)\\ \text{ mid-point }&&f(c_1)\cdot \, \Delta x &+&f(c_2)\cdot \, \Delta x &+&&...&&&+&f(c_{n})\cdot \, \Delta x \end{array}$$ The table shows the $n$th mid-point Riemann sum of $f$ on $[a,b]$.
The single formula representation of the mid-points is $$c_i=a+\left(i+\tfrac{1}{2}\right)\, \Delta x ,\ i=0,1,2,...,n-1.$$
Recall the sigma notation introduced in Chapter 1. The sum of a segment -- from $m$ to $n$ -- of a sequence $a_i$ is denoted by: $$a_m+a_{m+1}+...+a_n =\sum_{i=m}^{n}a_i.$$ Therefore, we have the following for the Riemann sum: $$f(c_{1})\, \Delta x_1 + f(c_{2}) \, \Delta x_2 + ... + f(c_{n})\, \Delta x_n= \sum_{i=1}^n f(c_i)\, \Delta x_i.$$ Taking into account the interval, this can also be seen as: $$\sum_{a\le c_i\le b} f(c_i)\, \Delta x_i.$$ Furthermore, a version of the sigma notation designed specifically for the Riemann sums is as follows: $$\sum_{[a,b]} f\, \Delta x,$$ with omitted subscripts.
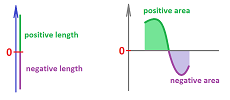
Example. When the region lies within the Euclidean plane, the $i$th term in all three Riemann sums is: $$\text{the area of }i\text{th rectangle} = \underbrace{f(c_{i})}_{\text{height of rectangle}} \cdot \overbrace{ \Delta x_i }^{\text{width of rectangle}}, $$ and the Riemann sum is total area of the rectangles. But what if the values of $f$ are negative, $$f(c_i)<0?$$ What is the meaning of each term $f(c_{i})\, \Delta x$ then? Just imagine again that $f$ is the velocity. Then $f(c_{i})\, \Delta x $ is still distance “covered” but with the negative speed, you are moving in the opposite direction! Then your displacement is negative. As for the area metaphor, since $\Delta x >0$, the meaning is determined by the meaning of $f(c_i)$:
$\square$
Now, even if the person didn't spend any time driving, the displacement still makes sense. It's zero! We extend then the meaning of the Riemann sum to include intervals of zero length.
Definition. The Riemann sum of a function $f$ over an augmented partition $P$ of a “zero-length” interval $[a,a]$, is defined to be zero: $$\sum_{[a,a]} f\, \Delta x =0.$$
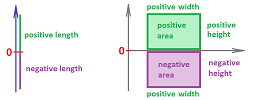
To capitalize on this idea even further, we extend the meaning of the integral to all oriented segments (as well as oriented rectangles, as defined in Chapter 4):
- $[a,b]$ is positively oriented when $a<b$ and
- $[a,b]$ is negatively oriented when $a>b$.
In the latter case, the length of the interval is the distance from $a$ to $b$, i.e., $b-a$, which is negative!
Definition. The Riemann sum of a function $f$ over a negatively oriented interval $[b,a], \ a\le b$, over an augmented partition $P$ of $[a,b]$, is defined to be the negative of the Riemann sum over $P$: $$\sum_{[b,a]} f\, \Delta x =-\sum_{[a,b]} f\, \Delta x.$$
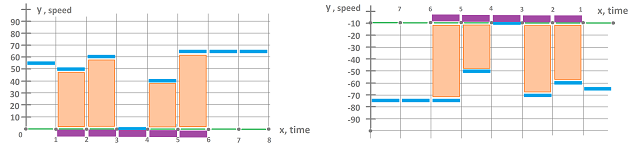
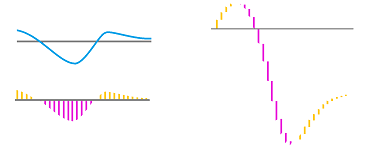
Example. When the region lies within the Euclidean plane, the width of the corresponding rectangle in the Riemann sum is also negative and so is its area when the function is positive:
The notion of a negative area is justified by the fact that the rectangle is negatively oriented... The motion metaphor might explain better though. It is as if time is reversed (or a videotape goes backward), so that the direction of motion is opposite, and all gains are reversed:
$\square$
We can also think of flipping an interval as multiplication by $-1$. If $I$ stands for such an interval, we have: $$\sum_{-I} f\, \Delta x =-\sum_{I} f\, \Delta x.$$
We next consider the simplest case of a Riemann sum.
Theorem (Constant Function Rule). Suppose $f$ is constant at the secondary nodes of a partition of $[a,b]$, i.e., $f(c_i) = p$ for all $i=1,2,...,n$ and some real number $p$. Then $$\sum_{[a,b]} f\, \Delta x = p ( b-a ). $$
Proof. Since $f(c_{i}) = p$ for all $i$, the Riemann sum is equal to: $$\begin{aligned} \sum_{[a,b]} f\, \Delta x &=f(c_{1})\, \Delta x_1+ f(c_{2}) \, \Delta x_2+...+f(c_{n}) \, \Delta x_n\\ &= p \, \Delta x_1+ p \, \Delta x_2+...+p \, \Delta x_n \\ &= p \big[ \Delta x_1+ \Delta x_2+...+\Delta x_n \big] \\ &=p \big[ (x_1-x_{0})+(x_2-x_{1})+ (x_3-x_{2})+...+(x_n-x_{n-1}) \big]\\ &= p(b-a). \end{aligned}$$ $\blacksquare$
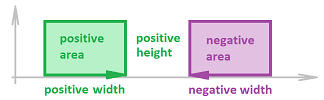
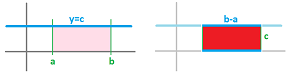
Once we zoomed out, we recognize that the Riemann sum represents the rectangle with width $b-a$ and height $p$:
Except, it is negative when $p$ is negative.
The Fundamental Theorem of Calculus
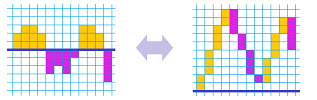
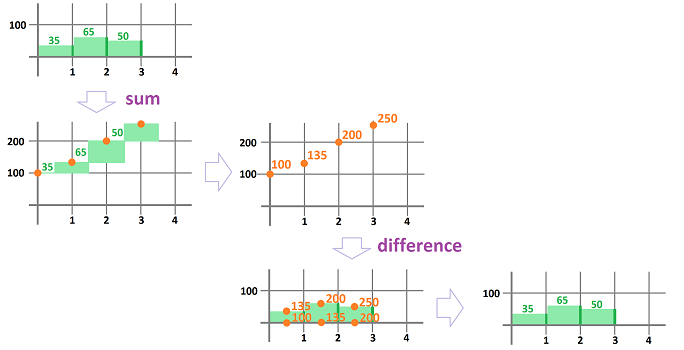
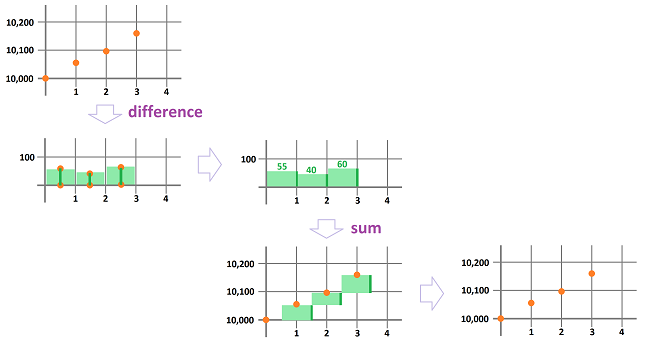
In Chapter 1 we noticed that the sum and the difference -- as operations on sequences -- cancel each other. We illustrate this idea with the following:
As you can see, the sum stacks up the terms of the sequence on top of each other while the difference takes this back down.
What the sum and the difference have to do with the Riemann sums and the difference quotients? Just plug in $\Delta x_k=1$ and you get the former from the latter, respectively. The relation between Riemann sums and difference quotients is fundamental.
Example. We know how to get velocity from the location -- and the location from the velocity. Of course, executing these two operations consecutively should bring us back where we started.
We now take another look at the two computations about motion -- a broken odometer and a broken speedometer -- presented earlier.
First, this is how we use the velocity function to acquire the displacement; but each of the values of the latter is the Riemann sum of the former:
Second, this is how we use the location function to acquire the velocity:
But each of the values of the latter is a difference quotient of the former! $\square$
Suppose once again that we have an augmented partition $P$ of an interval $[a,b]$ with $n$ intervals and
- the primary nodes: $x_k,\ k=0,1,...,n$;
- the lengths: $\Delta x_k=x_k-x_{k-1},\ i=1,2,...,n$; and
- the secondary nodes: $c_k,\ i=1,2,...,n$ in $[x_{k-1},x_k]$.
Suppose we have a function $g$ defined at the secondary nodes $c_k$. We compute its Riemann sum just as before but with a variable right end, $x_k$: $$\sum_{[a,x_k]} g\, \Delta x,\ k=1,2,..., n.$$ We assign these values to these primary nodes. This defines a new function, $G$, defined on the primary nodes. The new function can be written explicitly: $$G(x_{k})=\sum_{[a,x_k]} g\, \Delta x=g(c_{1})\, \Delta x_1 + g(c_{2}) \, \Delta x_2 + ... + g(c_{k})\, \Delta x_k,$$ or computed recursively: $$G(x_{k})=G(x_{k-1})+g(c_k)\, \Delta x_k.$$
Suppose we have a function $F$ defined at the primary nodes of the partition. Just as always, its difference quotient is computed over each interval $[x_{k-1},x_{k}]$ of the partition, as follows: $$\frac{F(x_{k})-F(x_{k-1})}{\Delta x_k},\ k=1,2...,n.$$ We then have a number -- representing a certain slope -- for each $k$. This defines a new function, $f$, on the secondary nodes. The new function is computed by an explicit formula: $$f(c_{k})=\frac{F(x_{k})-F(x_{k-1})}{\Delta x_k}.$$
The first question we would like to answer is, what is the difference quotient of the Riemann sum?
We have $g$ defined at the secondary nodes of the partition and its (variable-end) Riemann sum $G$ defined recursively at the primary nodes: $$G(x_{k})=G(x_{k-1})+g(c_{k})\, \Delta x_k.$$ Also, the difference quotient $f$ of $G$ is defined at the secondary nodes by: $$f(c_{k})=\frac{G(x_{k})-G(x_{k-1})}{\Delta x_k}.$$ We substitute the latter into the former: $$\begin{array}{lll} f(c_{k})&=\frac{G(x_{k})-G(x_{k-1})}{\Delta x_k}\\ &=\frac{g(c_k)\, \Delta x_k}{\Delta x_k}\\ &=g(c_k). \end{array}$$ So, the answer is, the original function.
Theorem (Fundamental Theorem of Discrete Calculus I). The difference quotient of the Riemann sum of $g$ is $g$: $$\frac{\Delta \left(\displaystyle\sum_{[a,x]} g\, \Delta x\right) }{\Delta x}=g.$$
The two operations cancel each other!
The second question we would like to answer is, what is the Riemann sum of the difference quotient?
We have $F$ defined at the primary nodes of the partition and its difference quotient $f$ defined at the secondary nodes: $$f(c_{k})=\frac{F(x_{k})-F(x_{k-1})}{\Delta x_k}.$$ Also, the Riemann sum $G$ of $f$ is defined at the primary nodes by: $$G(x_{k})=G(x_{k-1})+f(c_k)\, \Delta x_k.$$ We substitute the former into the latter: $$\begin{array}{lll} G(x_{k})-G(x_{k-1})&=f(c_k)\, \Delta x_k\\ &=\frac{F(x_{k})-F(x_{k-1})}{\Delta x_k}\, \Delta x_k\\ &=F(x_{k})-F(x_{k-1}). \end{array}$$ Furthermore, $$\begin{array}{lll} G(x_{k})-G(x_{0})&=\big[G(x_{k})-G(x_{k-1})\big]+\big[G(x_{k-1})-G(x_{k-2})\big]+...+\big[G(x_{1})-G(x_{0})\big]\\ &=\big[F(x_{k})-F(x_{k-1})\big]+\big[F(x_{k-1})-F(x_{k-2})\big]+...+\big[F(x_{1})-F(x_{0})\big]\\ &=F(x_{k})-F(x_{0}). \end{array}$$
So, the answer is, the original function plus a constant.
Theorem (Fundamental Theorem of Discrete Calculus II). The Riemann sum of the difference quotient of $F$ is $F+C$, where $C$ is a constant: $$\sum_{[a,x]}\left( \frac{\Delta F}{\Delta x} \right) \, \Delta x =F+C.$$
The two operations -- almost -- cancel each other, again!
The result shouldn't be surprising considering the operations involved: $$\left. \begin{array} {rccc} \text{difference quotient, } \frac{\Delta f}{\Delta x} :& \text{ subtraction } &\to & \text{ division } \\ & && &&\text{opposite!}\\ \text{Riemann sums, } \sum_{[a,x]} f\cdot \Delta x :& \text{ addition } &\gets & \text{ multiplication } \end{array} \right. $$
Warning: to the fact known from Chapter 1 -- sum and difference cancel each other -- we add multiplication and division by $\Delta x$.
Example. For complex data, we use a spreadsheet with the formulas presented in Chapters 6 and 7. From a function to its Riemann sum: $$\texttt{ =R[-1]C+RC[-1]*R1C2}\ .$$ From a function to its difference quotient: $$\texttt{ =(RC[-1]-R[-1]C[-1])/R1C2}\ .$$ What if we combine the two consecutively? In this order first, from a function to its Riemann sum to the difference quotient of the latter:
It's the same function! Now in the opposite order, from a function to its Riemann sum to the difference quotient of the latter:
It's the same function! $\square$
How to approximate areas and displacements
Example (triangle). Let's test the Riemann sum approach to computing areas to another familiar region, a triangle. Suppose $$f(x)=x.$$ What is the area under its graph from $x=0$ to $x=1$?
We plot this chart for different number values of $n$ let the spreadsheet to find the total area: $$\begin{array}{l|ll} n& 2&4 &8&16&80\\ \hline \Delta x & 1/2&1/4 &1/8&1/16&1/80\\ \hline D_n&0.250&0.375&0.438&0.469&0.494 \end{array}$$ For an arbitrary $n$, the total area is: $$\begin{array}{ccc} D_n &=& f(x_1)\cdot \Delta x &+& f(x_2)\cdot \Delta x &+&...&+&f(x_n)\cdot \Delta x \\ &=&\frac{1}{n}\cdot \frac{1}{n} &+&\frac{2}{n}\cdot \frac{1}{n} &+&...&+& \frac{n-1}{n}\cdot \frac{1}{n}&\text{ … factor...}\\ &=\bigg(& 1&+&2&+&...&+&(n-1) & \bigg)\cdot \frac{1}{n^2}. \end{array}$$ The formula for the expression in parentheses is known from Chapter 1: $$1+2+...+(n-1)=\frac{n(n-1)}{2}.$$ Therefore, the total area of the bars is the following limit: $$D_n=\frac{n(n-1)}{2}\frac{1}{n^2}=\frac{1}{2}\frac{n^2-n}{n^2}\to \frac{1}{2}\ \text{ as }n\to \infty,$$ according to Theorem Limits of Rational Functions (Chapter 5). The result matches what we know from geometry. $\square$
Note that we wouldn't be able to apply the rules and methods of computing limits without this simplification step. Unlike most sequences we saw in Chapter 5, the expression for the Riemann sum has $n$ terms. This means that we do not have a direct, or explicit, formula for the $n$th term of this sequence. Converting the former into the latter requires some challenging algebra. A few such formulas are known.
Theorem. The sums of $m$ consecutive numbers, their squares, and their cubes are the following: $$\begin{array}{ll} \sum_{k=1}^m k&=\frac{m(m+1)}{2},\\ \sum_{k=1}^m k^2&=\frac{m(m+1)(2m+1)}{6}&=\frac{m^3}{3}+\frac{m^2}{2}+\frac{m}{6},\\ \sum_{k=1}^m k^3&=\left(\frac{m(m+1)}{2}\right)^2&=\frac{m^4}{4}+\frac{m^3}{2}+\frac{m^2}{4}. \end{array}$$
Proof. The first one is proven in Chapter 1. $\square$
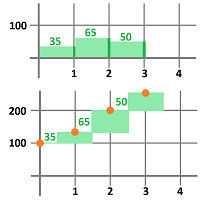
Example (squares). Problem: Suppose we are following a landing module in its trip to the moon. The very last part of the trip is very close to the surface and it is supposed to cover $2/3$ of a mile in one minute. Considering that there is no way to measure altitude above the surface, how would we know that it has landed?
This is what we do know: The velocity, at all times:
Solution: We approach the problem by predicting the displacement every:
- $1$ minute, or
- $1/2$ minute, or
- $1/4$ minute, or
- etc.,
by using the speed recorded at the beginning of each of these intervals: $$\text{projected displacement}= \text{initial velocity} \cdot \text{time passed}. $$
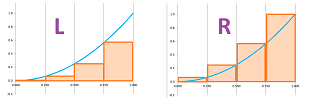
We have already plotted the velocity and now we are also to visualize the projected displacement. It is a plot of the same function but presented as a different kind of plot, a bar chart:
We plot this chart for different number of time intervals, $n$, and different choices of their lengths, $\Delta x =1/n$. We also let the spreadsheet add these numbers to produce the total displacement, $D_n$, over the whole one-minute interval. This is the data: $$\begin{array}{l|ll} n& 2&4 &8&16&80\\ \hline \Delta x & 1/2&1/4 &1/8&1/16&1/80\\ \hline D_n&0.869&0.778&0.725&0.697&0.673 \end{array}$$
The data suggests that the craft has landed as the estimated displacement seems to be close to $2/3$ miles. How close are we to this distance? As this question means different things to different people, let's try to find a rule for answering it: find the projected displacement $D_n$ as it depends on $n$.
First, the length of each time interval is: $$\Delta x =\frac{1}{n},$$ and the moments of time for sampling are: $$x_1=0,\ x_2=\frac{2}{n},\ x_3=\frac{3}{n},\ ...,\ x_n=\frac{n-1}{n}.$$
Furthermore, we need exact, complete data about the velocity. Suppose the velocity $y$ as a function of time, $x$, is given by this, exact formula: $$ y=f(x) =1-x^2 .$$ Then, the total displacement is: $$\begin{array}{ccc} D_n &=& &f(x_1)\cdot \Delta x & + &f(x_2)\cdot \Delta x &+&...&+&f(x_n)\cdot \Delta x \\ &=&&\left(1-\left(\frac{1}{n}\right)^2\right)\cdot \frac{1}{n} &+&\left(1-\left(\frac{2}{n}\right)^2\right)\cdot \frac{1}{n} &+&...&+& \left(1-\left(\frac{n-1}{n}\right)^2\right)\cdot \frac{1}{n}\\ &=&1-\bigg(& \frac{1^2}{n^2}&+&\frac{2^2}{n^2}&+&...&+&\frac{(n-1)^2}{n^2} &\bigg)\cdot \frac{1}{n}\\ &=&1-\bigg(& 1^2&+&2^2&+&...&+&(n-1)^2&\bigg)\cdot \frac{1}{n^3}. \end{array}$$
This is the sequence of improving approximations of the displacement! Let's simplify it using the last theorem: $$1^2+2^2+...+(n-1)^2=\frac{(n-1)^3}{3}+\frac{(n-1)^2}{2}+\frac{n-1}{6}.$$ Therefore, $$\begin{array}{lll} D_n&=1-\left( \frac{(n-1)^3}{3}+\frac{(n-1)^2}{2}+\frac{n-1}{6}\right)\frac{1}{n^3}\\ &=1-\frac{(n-1)^3}{3n^3}-\frac{(n-1)^2}{2n^3}-\frac{n-1}{6n^3}. \end{array}$$ With this formula, we can improve the accuracy of our approximation of the total displacement to any degree we desire by choosing larger and larger values of $n$.
Next, what is the exact displacement $D$? It is the limit of the sequence $D_n$. We apply Theorem Limits of Rational Functions (Chapter 5) and compare the leading terms of the two fractions: $$D_n\to 1-\frac{1}{3}-0-0=\frac{2}{3} .$$ $\square$
Exercise. Redo the example for $f(x)=x^2$.
Exercise. Use the last formula in the theorem to find the area under the graph of $y=x^3$.
Example. Let's estimate -- in several ways -- the area under the graph of $y = f(x) = x^{2}$ that lies above the interval $[0,1]$.
As before, we will sample our function at several values of $x$, a total of $n$ of times.
Let's start with $n=1$ and pick the right end of the interval as the only secondary node. Here, $f(1) = 1^{2} = 1$, the area is $1$, the whole square. We record this result as: $$R_1=1,$$ where $R$ stands for “right”.
In the meantime, if we choose the left end, we have $f(1) = 0^{2} = 0$, so the area is $0$. We record this result as: $$L_1=0,$$ where $L$ stands for “left”.
Next, $n=2$. Then $\Delta x =1/2$ and the interval is subdivided as follows: $$\begin{array}{r|cccccc} &\bullet&---&|&---&\bullet\\ x&0&&1/2&&1\\ f(x)=x^2&0&&1/4\\ L_2&0\cdot 1/2&+&1/4\cdot 1/2&&&&=1/8\\ R_2&&&1/4\cdot 1/2&+&1\cdot 1/2&&=5/8 \end{array}$$
Note that these two quantities underestimate and overestimate the area, respectively.
Now, $n=4$. Then $\Delta x =1/4$ and the interval is subdivided as follows: $$\begin{array}{r|cccccc} &\bullet&--&|&--&|&--&|&--&\bullet\\ x&0&&1/4&&1/2&&3/4&&1\\ x^2&0&&1/16&&1/4&&9/16&&1\\ L_4&0\cdot 1/4&+&1/16\cdot 1/4&+&1/4\cdot 1/4&+&9/16\cdot 1/4&& &\approx 0.22\\ R_4&&&1/16\cdot 1/4&+&1/4\cdot 1/4&+&9/16\cdot 1/4&+&1\cdot 1/4&\approx 0.47. \end{array}$$
Note that these two quantities underestimate and overestimate the area, respectively.
This is the algebraic representation of the computation in the table: $$ \begin{aligned} R_4&=\frac{1}{4}\cdot\frac{1}{16} + \frac{1}{4}\cdot\frac{1}{4} + \frac{1}{4}\cdot\frac{9}{16} + \frac{1}{4}\cdot 1\\ &= \frac{1}{4}\left( \frac{1}{16} + \frac{4}{16} + \frac{9}{16} + \frac{16}{16}\right) \\ &= \frac{1}{4} \, \frac{30}{16}\\ & \approx .47. \end{aligned}$$ $\square$
We continue with larger and larger values of $n$. We end up with a sequence of numbers. Then the limit of this sequence is meant to produce the area of this curved figure. These expressions are the Riemann sums of the function. They
- approximate the exact area, and
- their limit is the exact area.
Example. There are other Riemann sums if we choose other secondary nodes of the intervals, such as mid-points; it is denoted by $M_n$. Let's again estimate the area under $y = x^{2}$ with $n=4$. Since $L_4$ and $R_4$ underestimate or overestimate the area respectively, one might expect that $M_4$ will be closer to the truth.
The value of $\, \Delta x $ is still $1/4$: $$\begin{array}{r|cccccc} &\bullet&--&|&--&|&--&|&--&\bullet\\ x&&1/8&&3/8&&5/8&&7/8&\\ f(x)=x^2&&(1/8)^2&&(3/8)^2&&(5/8)^2&&(7/8)^2&\\ M_4&&(1/8)^2\cdot 1/4&+&(3/8)^2\cdot 1/4&+&(5/8)^2\cdot 1/4&+&(7/8)^2\cdot 1/4&\approx 0.328. \end{array}$$
$\square$
Exercise. Finish the sentence “$L_n$ and $R_n$ will continue to underestimate and overestimate the area no matter how many intervals we have because $f$ is...”
Exercise. Finish the sentence “$M_n$ will continue to underestimate the area no matter how many intervals we have because $f$ is...”
The limit of the Riemann sums: the Riemann integral
Suppose this time that a function $f$ is defined at all points of interval $[a,b]$.
Then $f$ has a Riemann sum for every augmented partition $P$ of $[a,b]$: $$a=x_0\le c_1\le x_1\le c_2\le x_2\le … <x_{n-1}\le c_1\le x_n=b,$$ Indeed, every Riemann sum is just this sum: $$\sum_{[a,b]} f\, \Delta x =f(c_{1})\, \Delta x_1+f(c_{2})\, \Delta x_2+...+f(c_{n})\, \Delta x_n =\sum_{i=1}^{n} f(c_{i})\, \Delta x_i, $$ where $$\Delta x _i=x_i-x_{i-1}.$$
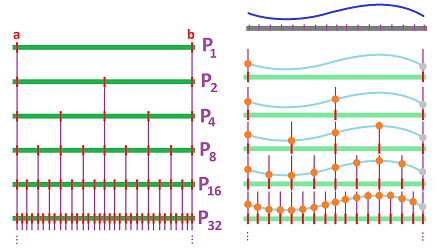
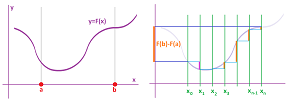
Now, in order improve these approximations, we refine the partition: there are more intervals and they are smaller. We keep refining. The result is a sequence of partitions, $P_n$. For example, we can cut every interval in half every time:
For every one of these partitions, we also choose a set of secondary nodes we use for sampling the function $f$ (left, right, middle, etc.). The result is what we can think of as a new function $f_n$. The Riemann sums of these functions, $$S_n=\sum_{[a,b]} f_n\, \Delta x,$$ form a numerical sequence, $S_n$.
This sequence may converge as $n\to \infty$!
The limit of this sequence, $\lim_{n\to \infty}S_n=S$, is what we are after. However, in the presence of infinitely many such sequences of partitions, we need to require that all of them produce the same number. $$\begin{array}{ccc} L_n && M_n && R_n\\ &\searrow &\downarrow& \swarrow\\ S_n & \to & S& \leftarrow&?\\ &\nearrow &\uparrow& \nwarrow\\ ? && ? && ?\ .\\ \end{array}$$
All these sequences of partitions have to be chosen in such a way that $$\Delta x_i \to 0\ \text{ as }\ n \to \infty.$$ To make sense of this, we define the mesh of a partition $P$ as: $$|P|=\max_i \, \, \Delta x _i.$$ It is a measure of the “refinement” of $P$.
Definition. The Riemann integral, or the definite integral, of a function $f$ over interval $[a,b]$ is defined to be the limit of a sequence of its Riemann sums with the mesh of their augmented partitions $P_n$ approaching $0$ as $n\to \infty$ when all these limits exist and are equal to each other. In that case, $f$ is called an integrable function over $[a,b]$ and the integral is denoted by: $$ \int_{a}^{b} f\, dx =\lim_{n \to \infty} \sum_{[a,b]} f_n\, \Delta x ,$$ where $f_n$ is $f$ sampled over the partition $P_n$. When all these limits are equal to $+\infty$ (or $-\infty$), we say that the integral is infinite and write: $$ \int_{a}^{b} f\, dx =+\infty\ (\text{or }-\infty).$$
Both can be seen as the areas under certain graphs and the Riemann integral is the limit of the Riemann sums, in this special sense.
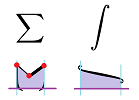
The symbol “$\int$” is called the integral sign. It looks like a stretched letter S, which stands for “summation” (as does letter $\Sigma$):
The notation is similar, because it is related, to that for Riemann sums (it is also similar, because it is related, to that for antiderivatives). This is how the notation is deconstructed: $$\text{domain}\Bigg[\begin{array}{rlrrll} \text{left}&\text{and right bounds for }x\\ \downarrow&\\ \begin{array}{r}1\\ \\-1\end{array}&\int \bigg(\quad 3x^{3} & + \sin x \quad\bigg)dx &=&0\\ &\uparrow&\uparrow&&\uparrow\\ &\text{left and}&\text{right parentheses}&&\text{a specific number} \end{array}$$ We refer to $a$ and $b$ as the lower bound and the upper bound of the integral, while $f$ is the integrand. The interval $[a,b]$ is referred to as the domain of integration.
Warning: other sources commonly use “limits” instead of “bounds”.
Exercise. What do those “bounds” have to do with the word “boundary”?
While $dx$ seems to be nothing but a “bookend” in the above notation, let's not forget that this is the differential. An alternative notation, that follows the notation for the Riemann sums, reflects the fact that the integral is a function determined by a differential form, $f(x)\cdot dx$, and, furthermore, the inputs of this function are intervals: $$ \int_{[a,b]} fdx = \int_{a}^{b} f\, dx ,$$ This is how the notation is deconstructed: $$\begin{array}{rcccll} &\text{“evaluate”}&\text{ }\\ &\downarrow&\\ &\int& \underbrace{\big( 3x^3 + \sin x \big)dx }&=&0\\ \text{input}\to&[-1,1]&\uparrow&&\uparrow\\ &\text{}&\text{differential form}&&\text{output} \end{array}$$
When we speak of the area, we have (with $n$ dependent on $k$): $$\underbrace{\int_{a}^{b} f\, dx}_{\text{the exact area under the graph}} = \lim_{k \to \infty}\underbrace{\sum_{i=1}^{n} f(c_{i})\, \Delta x _i}_{\text{areas of the bars}}. $$ In general, however, when the values of $f$ are negative so is the “area” under its graph:
Let's verify that the definition makes sense for the simplest function.
Theorem (Constant Integral Rule). Suppose $f$ is constant on $[a,b]$, i.e., $f(x) = c$ for all $x$ in $[a,b]$ and some real number $c$. Then $f$ is integrable on $[a,b]$ and $$\int_{a}^{b} f\, dx = c (b-a).$$
Proof. From the Constant Function Rule for Riemann sums, we know: $$\sum_{[a,b]} f_k\, \Delta x = c(b-a).$$ Since this expression doesn't depend on $k$, the conclusion follows. $\blacksquare$
Of course, we have recovered the formula for the area of a rectangle: $$\text{area }=\text{ height }\cdot \text{ width}.$$ Except, this area is negative when $c$ is negative.
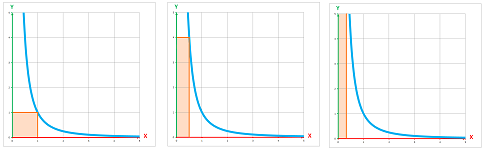
Example. Here is a simple example of a function non-integrable over $[0,1]$: $$f(x)=\begin{cases}\frac{1}{x^2}&\text{ if } x>0;\\ 0&\text{ if } x=0.\end{cases}$$ It suffices to look at the first term of the $k$th right-end Riemann sum: $$f(x_1)\, \Delta x = f\left(\frac{1}{k}\right)\frac{1}{k}=\frac{1}{1/k^2}\frac{1}{k}=k\to \infty \text{ as } k\to \infty.$$ It turns out this bar is getting taller faster than it is getting thinner!
Then, from the Push Out Theorem for divergence (Chapter 5), it follows that $$R_k\to \infty \text{ as } k\to\infty.$$ Therefore, $$ \int_{0}^{1} f\, dx =+\infty.$$ $\square$
Exercise. Consider this construction for $\tfrac{1}{x}$ and $\tfrac{1}{x^3}$.
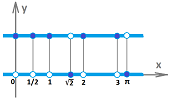
Example. The Dirichlet function is also non-integrable: $$I_Q(x)=\begin{cases} 1 &\text{ if }x \text{ is a rational number},\\ 0 &\text{ if }x \text{ is an irrational number}. \end{cases}$$
Indeed,
- if we choose all the secondary nodes of partitions $P_n$ to be rational, the corresponding Riemann sums will be equal to $1$; therefore, the limit will be equal to $b-a$; but
- if we choose all the secondary nodes of partitions $P_n$ to be irrational, the corresponding Riemann sums will be equal to $0$; therefore, the limit is also equal to $0$.
$\square$
The following result proves that our definition makes sense for a large class of functions.
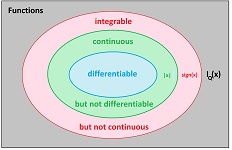
Theorem. All continuous functions on $[a,b]$ are integrable on $[a,b]$.
We accept it without proof.
The converse isn't true because of the following.
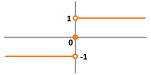
Example (sign function). The sign function, $f(x)=\operatorname{sign}(x)$, has a very simple graph and, it appears, the area under it would “make sense”:
Indeed, this function is integrable over any interval $[a,b]$. There are two cases. When $b\le 0$ or $a\ge 0$, the function is simply constant on this interval. When $a<0<b$, all terms of all Riemann sums are $-1\cdot \, \Delta x_i$, or $1\cdot \Delta x _i$, or $0$ (at most two). Let's suppose that $0$ isn't a node of any of the partitions $P_k$ and, in fact, it is one of its secondary nodes, $0=c_m$. Then $$\begin{array}{lll} \sum_{[a,b]} f\, \Delta x &=\sum_{i=1}^{m-1}(-1)\cdot \Delta x _{i}&+0\cdot \Delta x _{m}&+ \sum_{i=m+1}^{n} 1\cdot\Delta x_{i}\\ &=-\sum_{i=1}^{m-1}\, \Delta x_{i}&&+ \sum_{i=m+1}^{n}\, \Delta x_{i}\\ &=-(x_m-a)&&+(b-x_{m+1})\\ &=a+b&-x_m-x_{m+1}. \end{array}$$ Then, as $|P_k|\to 0$, we have: $$x_m\to 0 \text{ and } x_{m+1}\to 0.$$ Therefore, the equation's limit is: $$\int_a^b f\,dx=a+b.$$ $\square$
Exercise. Consider the missing cases in the above proof.
Just as before, we observe that even if the person didn't spend any time driving, the displacement makes sense; it's zero.
Theorem. The Riemann integral of a function $f$ over a “zero-length” interval $[a,a]$, is equal to zero: $$\int_{a}^{a} f\, dx =0.$$
Exercise. Prove the theorem.
The oriented intervals are also included.
We once again utilize the idea of oriented intervals and oriented rectangles.
Theorem. The Riemann integral of a function $f$ over a negatively oriented interval $[b,a],\ b>a$ is equal to the negative of the integral over $[a,b]$: $$\int_{b}^{a} f\, dx =-\int_{a}^{b} f\, dx .$$
Exercise. Prove the theorem.
In the differential form notation, the theorem is as follows: $$\int_{-[a,b]} fdx =-\int_{[a,b]} fdx.$$
Thus, we have explained the meaning of the area. It is an integral. Conversely, is the integral an area? Yes, in a sense. It depends on the units of the variables. For example, when both $x$ and $y$ are measured in feet, the integral is indeed the area in the usual sense; it is measured in square feet. However, what if $x$ and $y$ are something else? We have already seen that $x$ may be time and $y$ the velocity; they are measured in seconds and feet per second respectively. Then the integral is measured in seconds $\cdot$ feet per second, i.e., feet. That can't be area... In fact, both $x$ and $y$ may be quantities of arbitrary nature; then the units of the integral might be: pound $\cdot$ degree, man-hour, etc. Then the integral is described as “the total value” of the function.
We accept the following result without proof.
Theorem. If $f$ is integrable over $[a,b]$ then it is also integrable over any $[A,B]$ with $a\le A < B \le b$.
Properties of the Riemann sums and the Riemann integrals
The properties of the Riemann sums come from pure algebra. It then remains to make sure that those relations are preserved under the limit to produce the matching properties of the Riemann integrals. The integral follows the Riemann sum, every time:
The formula of the Riemann sum is: $$\sum_{[a,b]} f\, \Delta x =f(c_1)\, \Delta x _1+f(c_2)\, \Delta x _2+... +f(c_n)\, \Delta x _n, $$ where the points $$a=x_0\le c_1\le x_1\le c_2\le x_2\le ...\le c_n\le x_n=b$$ make up an augmented partition of $[a,b]$. But it remains just a sum... We, therefore, can use some of the very elementary facts we learned about them in Chapter 1.
While adding, we can re-group the terms freely; in particular, we can remove the parentheses: $$(u_1+u_2+...+u_n)+(v_1+v_2+...+v_m)=u_1+u_2+...+u_n+v_1+v_2+...+v_m.$$ That's the Additivity Rule for Sums we saw in Chapter 1. What if these sums are Riemann sums? If we have partitions of two adjacent intervals, we can just continue to add terms creating a “longer” Riemann sum:
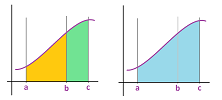
Theorem (Additivity). (A) The sum of the Riemann sums over two consecutive parts of an interval is the Riemann sum over the whole interval; i.e., for any function $f$ and for any $a,b,c$, we have: $$\sum_{[a,b]} f\, \Delta x +\sum_{[b,c]} f\, \Delta x = \sum_{[a,c]} f \, \Delta x ,$$ where the summations are over augmented partitions of $[a,b]$, $[b,c]$, and $[a,c]$ respectively. (B) The sum of the integrals over two consecutive parts of an interval is the integral over the whole interval; i.e., for any function $f$ integrable over $[a,b]$ and over $[b,c]$ is also integrable $[a,c]$ and we have: $$\int_a^b f\, dx +\int_b^c f\, dx = \int_a^c f\, dx.$$
Proof. Suppose the two augmented partitions, $P$ and $Q$, are given by: $$P:\quad a=x_0\le c_1\le x_1\le c_2\le x_2\le ...\le c_n\le x_n=b;$$ $$Q:\quad b=y_0\le d_1\le y_1\le d_2\le y_2\le ...\le d_m\le x_m=c.$$ We rename the items on the latter list and form an augmented partition of $[a,c]$: $$P\cup Q:\ a=x_0\le c_1\le x_1\le c_2\le x_2\le ...\le c_n\le x_n\le c_{n+1}\le x_{n+1}\le c_{n+2}\le x_{n+2}\le ...\le c_{n+m}\le x_{n+m}=c.$$ Applying the definition to the intervals $[a,b]$ and $[b,c]$ and then to $[a,c]$, we have: $$\begin{array}{ll} \sum_{[a,b]} f\, \Delta x +\sum_{[b,c]} f\, \Delta x &= \left( f(c_1)+f(c_2)+...+f(c_n) \right) \\ &+\left( f(c_{n+1})+f(c_{n+2})+...+f(c_{n+m}) \right)\\ &=\sum_{[a,c]} f \, \Delta x . \end{array}$$ This gives us part (A). For part (B), the integrability follows from the last theorem. To prove the formula, we start with this fact about the mesh of partitions: $$|P\cup Q|=\max \{|P|,|Q|\}.$$ Once we move to sequence of partitions, this fact implies the following: $$|P_k\cup Q_k|\to 0\ \Longleftrightarrow\ \ |P_k|\to 0\text{ and }|Q_k|\to 0.$$ Next, we take the formula in part (A), the Additivity Rule for Riemann sums, take the limit with $k\to \infty$ and use the Sum Rule for limits from Chapter 5. $\blacksquare$
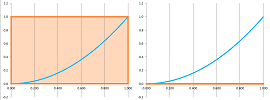
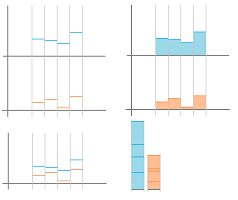
For the area metaphor, imagine that we have zoomed out of the picture of the Riemann sums. The result is equally applicable to the integrals; the formula in the theorem adds the areas of these two adjacent regions:
Here we have simply, $$\begin{array}{lll} \sum_{[a,b]} f\, \Delta x &+& \sum_{[b,c]} f\, \Delta x &=& \sum_{[a,c]} f\, \Delta x,\\ \text{ orange }&+ &\text{ green }&= &\text{ blue }. \end{array}$$
As you can see, the word “additivity” in the name of the theorem doesn't refer to adding the terms of the Riemann sums but to adding the domains of integration, i.e., the union of the two intervals. The idea becomes especially vivid when the formula is written in the differential form notation: $$\int_{[a,b]} fdx +\int_{[b,c]} fdx = \int_{[a,b]\cup [b,c]} fdx.$$ The interval becomes the input variable...
Exercise. Finish the formula: $$\int_{[a,b]} f\, dx +\int_{[c,d]} f\, dx = ...$$
For the motion metaphor, we have: $$\begin{array}{lll} &\text{distance covered during the 1st hour }\\ +&\text{distance covered during the 2nd hour }\\ =&\text{distance during the two hours}. \end{array}$$
The following is an important corollary.
Theorem (Integrability). All piece-wise continuous functions are integrable.
Proof. It follows from the integrability of continuous functions (last section) and the Additivity Rule. $\blacksquare$
In particular, all step-functions are integrable... After all, they even look like Riemann sums:
As you can see, the properties of Riemann integrals follow from the corresponding properties of the Riemann sums -- via the corresponding rules of limits. The graphical interpretations of the two properties are also the same; we just zoom out.
Suppose we have the right-end sum; there are $n$ intervals of equal length: $$\, \Delta x _i=h=\frac{b-a}{n}$$ between $a$ and $b$ and these are the secondary nodes: $$c_i=\ a,\ a+h,\ ...,\ b-h.$$ A proof for left-end sum and mid-points sums would be virtually identical.
Below, we will be reviewing some facts about sums presented in Chapter 1 and then applying them to the Riemann sums producing, via limits, results about the Riemann integrals.
Can we compare the values of two Riemann sums? Consider this simple algebra: $$\begin{array}{lll} u&\le&U,\\ v&\le&V,\\ \hline u+v&\le&U+V.\\ \end{array}$$ We can keep adding terms: $$\begin{array}{rcl} u_p&\le&U_p,\\ u_{p+1}&\le&U_{p+1},\\ \vdots&\vdots&\vdots\\ u_q&\le&U_q,\\ \hline u_p+...+u_q&\le&U_p+...+U_q,\\ \sum_{n=p}^{q} u_n &\le&\sum_{n=p}^{q} U_n. \end{array}$$ That's the Comparison Rule for Sums we saw in Chapter 1. What if these sums are Riemann sums?
Then, if one function “dominates” another, then so does its Riemann sum, and the integral:
Theorem (Comparison Rule). (A) The Riemann sum of a smaller function is smaller; i.e., if $f$ and $g$ are functions, then for any $a,b$ with $a<b$, we have: $$f(x)\geq g(x) \text{ on } [a,b] \ \Longrightarrow\ \sum_{[a,b]} f\, \Delta x \geq \sum_{[a,b]} g\, \Delta x $$ (B) The integral of a smaller function is smaller; i.e., if $f$ and $g$ are functions, then for any $a,b$ with $a<b$, we have: $$f(x)\geq g(x) \text{ on } [a,b] \ \Longrightarrow\ \int_{a}^{b} f\, dx \geq \int_{a}^{b} g\, dx,$$ provided $f$ and $g$ are integrable over $[a,b]$.
Proof. Applying the definition of the Riemann sum to the function $f$ and then to $g$, we have: $$\begin{array}{ll} \sum_{[a,b]} f\, \Delta x &= f(a)+f(a+h)+f(a+2h)+...+f(b-h)\\ &\ge g(a)+g(a+h)+g(a+2h)+...+g(b-h)\\ &=\sum_{[a,b]} g\, \Delta x . \end{array}$$ This gives us the inequality of part (A). Now take the limit with $n\to \infty$ and use the Comparison Rule for limits from Chapter 5. $\blacksquare$
If we zoom out, we see that the larger function always contains a larger area under its graph:
There is also a simple interpretation of this result in terms of motion: the faster covers the longer distance.
Exercise. Prove the rest of the theorem.
Exercise. Modify the proof for: (a) left-end, (b) mid-point, and (c) general Riemann sums.
Exercise. What happens when $a>b$?
A related result is the following.
Theorem (Strict Comparison Rule). Suppose $f$ and $g$ are functions. For any $a,b$ with $a<b$, we have: $$f(x)< g(x) \text{ on } [a,b] \ \Longrightarrow\ \sum_{[a,b]} f\, \Delta x < \sum_{[a,b]} g\, \Delta x .$$
Exercise. State and prove the Strict Comparison Rule for integrals. Hint: there is no Strict Comparison Rule for limits.
What if we know only a priori bounds of the function? Suppose the range of a function $f$ lies within the interval $[m,M]$. Then its graph lies between the horizontal lines $y=m$ and $y=M$, with $m<M$.
Then, what can we say about the Riemann sum of $f$? We would like to find an estimate for the area of the orange region in terms of $a$, $b$, $m$, $M$. Below, the yellow region on the left is less than the orange area. On the right, the green area is larger.
Furthermore, these two regions are rectangles and their areas are easy to compute. We use the following inequalities: $$\text{the area of the smaller rectangle}\leq \text{the area under the graph} \leq \text{the area of the larger rectangle}.$$ For the general case, we have the following.
Theorem (Bounds). Suppose $f$ is a function and suppose that for any $a,b$ with $a<b$, we have: $$m \leq f(x)\leq M,$$ for all $x$ with $a\le x \le b$. (A) Then $$m(b-a)\leq \sum_{[a,b]} f\, \Delta x \leq M(b-a).$$ (B) If $f$ is an integrable function over $[a,b]$, then $$m(b-a)\leq \int_{a}^{b} f\, dx \leq M(b-a).$$
Proof. For either of the two inequalities, we apply the Constant Function Rule from the last section and the Comparison Theorem above. This gives us the inequalities in part (A). Now take the limit with $k\to \infty$ and use the Bounds Rule for limits from Chapter 5. $\blacksquare$
Exercise. State and prove the Strict Estimate Rule.
Example. We know, a priori, that the values of such a trigonometric function as $\sin$ (and $\cos$) lie within $[-1,1]$. Then, we have: $$\begin{array}{rcccl} -1&\le &\sin x &\le &1& \text{ for all } x\quad\Longrightarrow\\ -1(b-a)&\le& \int_{a}^{b} \sin x\, dx &\le& 1(b-a). \end{array}$$ So, even though all we know about the function is just these two, very crude, estimates, we guarantee that the integral will lie within the interval $[a-b,b-a]$! $\square$
Now, the algebraic properties... They match some of the algebraic properties of the derivatives and both come from the algebraic properties of the limits.
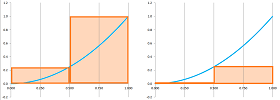
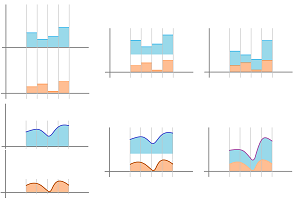
When two functions are added, what happens to their Riemann sums? This simple algebra tells the whole story: $$\begin{array}{lll} &u&+&U,\\ +\\ &v&+&V,\\ \hline =&(u+v)&+&(U+V).\\ \end{array}$$ The rule applies even if we have more than just two terms; it's just re-arranging terms: $$\begin{array}{rcl} u_p&+&U_p,\\ u_{p+1}&+&U_{p+1},\\ \vdots&\vdots&\vdots\\ u_q&+&U_q,\\ \hline u_p+...+u_q&+&U_p+...+U_q,\\ =(u_p+U_p)+&...&+(u_q+U_q),\\ =\sum_{n=p}^{q} (u_n &+&U_n). \end{array}$$ That's the Sum Rule for Sums we saw in Chapter 1. These sums might be Riemann sums... For the Riemann sums, the interpretation is simple; the picture below illustrates how adding two functions causes adding the areas under their graphs:
Theorem (Sum Rule). (A) The sum of the Riemann sums of two functions is the Riemann sum of the sum of the functions; i.e., if $f$ and $g$ are functions, then for any $a,b$, we have: $$\sum_{[a,b]} \left( f + g \right) \, \Delta x = \sum_{[a,b]} f\, \Delta x + \sum_{[a,b]} g\, \Delta x . $$ (B) The sum of the integrals of two functions is the integral of the sum of the functions; i.e., if $f$ and $g$ are integrable functions over $[a,b]$, then so is $f+g$ and we have: $$\int_{a}^{b} \left( f + g \right)\, dx = \int_{a}^{b} f\, dx + \int_{a}^{b} g\, dx. $$
Proof. Applying the definition to the function $y=f(x)+g(x)$, we have: $$\begin{array}{ll} \sum_{[a,b]} \left( f + g \right) \, \Delta x &= \left( f(a)+ g(a) \right)+\left( f(a+h)+g(a+h) \right)+...\\ &+\left( f(b-h) + g(b-h) \right)\\ &=\left( f(a)+f(a+h)+f(a+2h)+...+f(b-h,b) \right)\\ &+\left( g(a)+g(a+h)+g(a+2h)+...+g(b-h,b) \right)\\ &=\sum_{[a,b]} f\, \Delta x + \sum_{[a,b]} g\, \Delta x . \end{array}$$ This gives us part (A), the Sum Rule for Riemann sums. Now take the limit with $k\to \infty$ and use the Sum Rule for limits from Chapter 5. $\blacksquare$
The integral is split in half!
It is as if one is playing a game of Tetris:
The picture below illustrates what happens when the bottom drops from a bucket of sand and it falls on a curved surface:
For the motion metaphor, if two runners are running away from a post, their velocities are added and so are their distances to the post.
Exercise. Modify the proof for: (a) left-end, (b) mid-point, and (c) general Riemann sums.
Next, when a function is multiplied by a constant, what happens to its Riemann sums? This simple algebra, the Distributive Property, tells the whole story: $$\begin{array}{lll} c\cdot(&u&+&U)\\ =&cu&+&cU.\\ \end{array}$$ The rule applies even if we have more than just two terms; it's just factoring: $$\begin{array}{rcl} c&\cdot&u_p,\\ c&\cdot&u_{p+1},\\ \vdots&\vdots&\vdots\\ c&\cdot&u_q,\\ \hline c&\cdot&(u_p+...+u_q),\\ =c&\cdot&\sum_{n=p}^{q} u_n. \end{array}$$ That's the Constant Multiple for Sums we saw in Chapter 1. For the Riemann sums, the interpretation is simple; the picture below illustrates the idea of multiplication of the function viz. multiplication of the area under its graph:
Theorem (Constant Multiple Rule). (A) The Riemann sum of a multiple of a function is the multiple of its Riemann sum; i.e., if $f$ is a function, then for any $a,b$ and any real $c$, we have: $$ \sum_{[a,b]} (c\cdot f) \, \Delta x = c \cdot \sum_{[a,b]} f\, \Delta x .$$ (B) The integral of a multiple of a function is the multiple of its integral; i.e., if $f$ is an integrable function over $[a,b]$, then so is $c\cdot f$ for any real $c$ and we have: $$ \int_{a}^{b} (c\cdot f)\, dx = c \cdot \int_{a}^{b} f\, dx.$$
Proof. Applying the definition to the function $f(x)$, we have: $$\begin{array}{ll} \sum_{[a,b]} (c \cdot f) \, \Delta x &= c \cdot f(a)+c \cdot f(a+h)+c\cdot f(a+2h)+...+c \cdot f(b-h)\\ &=c \cdot \left( f(a)+f(a+h)+f(a+2h)+...+f(b-h) \right)\\ &=c \, \sum_{[a,b]} f\, \Delta x . \end{array}$$ This gives us part (A), the Constant Multiple Rule for Riemann sums. Now take the limit with $k\to \infty$ and use the Constant Multiple Rule for limits from Chapter 5. $\blacksquare$
The constant multiple is factored out of the integral!
It is as if one is playing a game of Tetris:
The picture below illustrates the idea that tripling the height of a road will need tripling the amount of soil under it:
For the motion metaphor, if your velocity is tripled, then so is the distance you have covered.
Exercise. Modify the proof for: (a) left-end, (b) mid-point, and (c) general Riemann sums.
The Fundamental Theorem of Calculus, continued
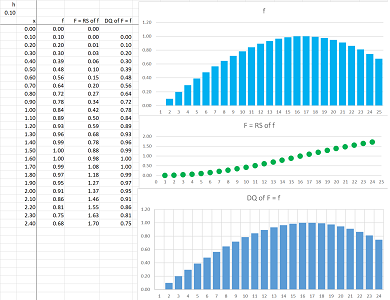
In this chapter, we have learned that the difference quotient and the Riemann sum undo the effect of each other. Since the derivative and the Riemann are the limits of these two respectively, it stands to reason that they have the same relation. Below, the Riemann integral of a function is approximated by the Riemann sum, the “partial sums” of which form a function:
This function approximates the derivative of the function!
So, what does the Riemann integral have to do with antiderivatives? Same as what the Riemann sum does!
We already know the answer, for the motion metaphor. If $y = f(x)$ is the velocity and $x$ time, then
- one antiderivative is the position function, $F(x)$;
- the integral the displacement during $[a,b]$, $\int\limits_{a}^{b} f\, dx$.
If we know the position at all times, we can certainly compute the displacement at any moment: $$\underbrace{F(b)}_{\text{current position}} - \underbrace{F(a)}_{\text{initial position}}.$$ Conversely, the displacement is found for any $x>a$ as $\int\limits_{a}^{x} f\, dx$.
Now, what about the area metaphor?
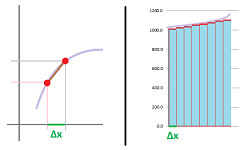
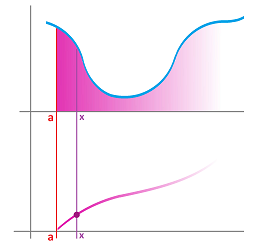
Analogous to what we did above for the Riemann sum, we define the area function of $f$ at $a$ to be: $$A(x) = \int\limits_{a}^{\overbrace{x}^{\text{varies}}} f(t) \, dt=\ \text{ area under the graph over }[a,x].$$ This is the familiar Riemann integral but with a variable upper bound. It's also illustrated below: $x$ runs from $a$ to $b$ and beyond.
We can see how, wherever $f$ has positive values, every increase of $x>a$ adds a slice to the area -- less in the middle -- causing $A$ to increase -- slower in the middle. Moreover, wherever $f$ has negative values, this slice will have a negative area thereby causing $A$ to decrease. That's a behavior of an antiderivative of $f$!
Exercise. Sketch the graph of the area function of function $f$ plotted below for $a=1$:
Exercise. Sketch the graph of a function of the area function of which is plotted above.
Exercise. Prove that the area function is continuous.
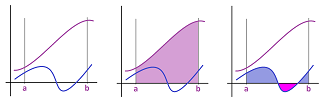
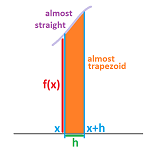
Let's consider its derivative, $A'$. We go all the way back to the definition of the derivative: $$\begin{aligned} A'(x) &= \lim_{h \to 0}\frac{A(x+h) - A(x)}{h} \\ &= \lim_{h \to 0} \frac{1}{h} \left( \int_{a}^{x+h} f\, dt - \int_{a}^{x} f\, dt\right) \\ &= \lim_{h \to 0} \frac{1}{h} \int_{x}^{x+h} f \, dx ,\\ \end{aligned}$$ by the Additivity Rule in the last section. In other words, we are left with a slice of the area above the segment $[x,x+h]$; it looks like a trapezoid when $h$ is small:
What happens to this limit? Let's make $h$ small. The “trapezoid” will be thinner and thinner and its top edge will look more and more straight, assuming $f$ is continuous. We know that the area of a trapezoid is the length of the mid-line times the height. Then we have: $$\frac{\text{area of trapezoid}}{\text{width}} = \text{ height in the middle}.$$ It follows that its height is approximated by: $$\frac{\int_{x}^{x+h} f\, dx }{h}. $$ This outcome suggests that $A'=f$. However, proving that the limit exists would require a subtler argument...
Exercise. Finish the proof by using the Squeeze Theorem for: $$f(x)\le \frac{A(x+h) - A(x)}{h}\le f(x+h).$$
Example (tringle). Let's confirm the idea with a familiar shape. Consider $$f(x) = 2x.$$ Let's compute the area function.
We have: $$\begin{aligned} A(x) &= \int_{0}^{x} 2x\, dx \\ &= \text{area of triangle} \\ &= \frac{1}{2} \text{width}\cdot\text{height} \\ &= \frac{1}{2} x \cdot 2x \\ &= x^{2}. \end{aligned}$$ What's the relation between $f(x) = 2x$ and $A(x) = x^{2}$? We know the answer: $$\left(x^{2}\right)' = 2x, $$ so $f$ is an antiderivative of $f$! $\square$
This idea applies to all functions.
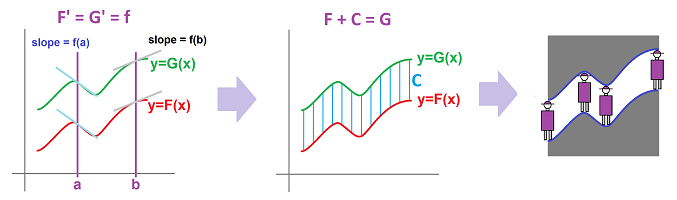
Theorem (Fundamental Theorem of Calculus I). Given a continuous function $f$ on $[a,b]$, the function defined by $$F(x) = \int_{a}^{x} f \, dx $$ is an antiderivative of $f$ on $(a,b)$.
Exercise. Derive the theorem from the Fundamental Theorem of Discrete Calculus.
Thus, differentiation cancels the effect of the (variable-end) Riemann integral: $F'=f$.
The theorem supplies us with a special choice of antiderivative -- the one that satisfies $F(a)=0$.
The rest, as we know, are acquired by vertical shifts: $G=F+C$.
Exercise. Find a formula for the antiderivative with $F(a)=1$.
Exercise. Find the derivative of $\int_x^b f\, dx $.
Next, we see how the Riemann integral cancels -- up to a constant -- the effect of differentiation.
Theorem (Fundamental Theorem of Calculus II). For any integrable function $f$ on $[a,b]$ and any of its antiderivatives $F$, we have $$\int_{a}^{b} f \, dx =F(b)-F(a).$$
Proof. We start with a partition $P$ of interval $[a,b]$ with $n$ intervals. The nodes $x_i,\ i=0,1,...,n,$ can be arbitrary; we can even choose equal lengths for the intervals: $\Delta x_i=x_i-x_{i-1}=(b-a)/n,\ i=1,2,...,n$. There are no secondary nodes yet; their choice will be dictated by $F$.
This is how each of the secondary nodes $c_i,\ i=1,2,...,n,$ is chosen:
Let's take one interval $[x_{i-1},x_{i}]$ and we apply the Mean Value Theorem to $F$: there is a $c_i$ in the interval such that $$\frac{F(x_{i})-F(x_{i-1})}{x_{i}-x_{i-1}}=F'(c_i).$$ In other words, we find a point within each interval that has the slope of its tangent line equal to the slope of the secant line over the whole interval $[x_{i-1},x_{i}]$:
We modify the formula: $$F(x_{i})-F(x_{i-1})=f(c_i)\, \Delta x.$$ This way
- the left-hand side is the net change (the rise) of $F$ over the interval $[x_{i-1},x_{i}]$, and
- the right-hand side is the element of the Riemann sum of $f$ over $[x_{i-1},x_{i}]$.
The next step is to express the total net change of $F$ over the interval $[a,b]$ as the sum of the net changes over the intervals of the partition:
We now convert those net changes according to the above formula: $$\begin{array}{lll} F(b)-F(a)&=F(x_{n})&=&\ \ \ F(x_{n})-F(x_{n-1})&=&\qquad\ \ \ f(c_n)\, \Delta x \\ & &&+F(x_{n-1})-F(x_{n-2}) &&\qquad + f(c_{n-1})\, \Delta x \\ & &&+... &&\qquad+...\\ & &&+F(x_{i+1})-F(x_i) &&\qquad + f(c_i)\, \Delta x \\ & &&+... &&\qquad+...\\ & \qquad\qquad -F(x_0) &&+F(x_{1})-F(x_0) &&\qquad + f(c_1)\, \Delta x . \\ \end{array}$$ The last expression is the Riemann sum of $f$ and, since $f$ is integrable, it converges to $\int_a^b\, f\, dx$ as $\, \Delta x \to 0$. $\blacksquare$
The theorem is also known as the Newton-Leibniz formula.
Exercise. Use the sigma notation to re-write the last computation.
Note: We can derive the Fundamental Theorem of Calculus I from the Fundamental Theorem of Calculus II (NLF) easily: $$\frac{d}{dx}\left( \int_a^x f\, dx \right)=\frac{d}{dx}\left( F(x)-F(a) \right)=F'(x)=f(x).$$
Warning: since the theorem applies to all antiderivatives, we can omit “$+C$”.
Example (parabola). Let's test the formula on the integral we did the hard way, via the Riemann sums; we compute the area under $y=x^{2}$ from $0$ to $1$.
We need the antiderivative of $f(x) = x^{2}$. By the Power Formula from Chapter 9: $$F(x) = \frac{x^{3}}{3}.$$ Then, by NLF, we have: $$\int_{0}^{1} x^{2}\, dx = F(1) - F(0) = \frac{1^{3}}{3} - \frac{0^{3}}{3} = \frac{1}{3}.$$ Easy in comparison to the Riemann sum approximation! $\square$
Recall the substitution notation: $$F(x)\Bigg|_{x=a}=F(a).$$ In its sprit, we introduce new notation for two substitutions: $$F(x) \Bigg|_{a}^{b}= F(b) - F(a).$$ Then, $$\int_{a}^{b} f \, dx = F(x) \Bigg|_{a}^{b}= F(b) - F(a).$$ As you can see, the bounds of integration just jump over and are kept for reference. This is how we can record the above computation: $$\int_{0}^{1} x^{2}\, dx = \frac{x^{3}}{3}\Bigg|_{0}^{1}.$$
Example (exponent). Computations of areas become easy -- as long as we have their antiderivatives.
Compute the area under $y=e^{x}$ from $0$ to $1$. By NLF, we have: $$\int_{0}^{1} e^{x} \, dx = e^{x} \Bigg|_{0}^{1}= e^{1} - e^{0} = e - 1.$$ $\square$
Example (cosine). Compute the area under $y=\cos x$ from $0$ to $\pi/2$.
$$\int_{0}^{\frac{\pi}{2}} \cos x \, dx = \sin x \Bigg|_{0}^{\frac{\pi}{2}} = \sin \frac{\pi}{2} - \sin 0 = 1 - 0 = 1.$$ $\square$
Example (circle). What is the area of a circle of radius $R$? Even though everyone knows the answer, this is the time to prove the formula. We also gave an approximate answer in the beginning of this chapter.
We first put the center of the circle at the origin of the $xy$-plane.
In order to find its area, we represent the upper half of the circle are the area under the graph of $$f(x)=\sqrt{R^2 - x^{2}},\ -R\le x\le R.$$ Then, $$\frac{1}{2}\text{Area } = \int_{-R}^{R} \sqrt{R^2 - x^{2}} \, dx .$$ What's the antiderivative of this function? Unfortunately, we don't know; it's not on our -- very short -- list. When this happens, we always do the same thing: we go to the back of the book to find a longer list. This list contains the relevant formula: $$\int \sqrt{a^2 - u^{2}} \, dx =\frac{u}{2}\sqrt{a^2 - u^{2}}+\frac{a^2}{2}\sin^{-1}\frac{u}{a}+C.$$
Now, even though we get the integration formula from elsewhere, once we have it, we can certainly prove it -- by differentiation. These two derivatives we know from Chapter 8: $$\left(\sqrt{a^2 - u^2}\right)'=-\frac{u}{\sqrt{a^2 - u^2}}\ \text{ and }\ \left(\sin^{-1}y \right)'= \frac{1}{\sqrt{1 - y^2}}.$$ Therefore $$\begin{array}{lllll} \left( \frac{u}{2}\sqrt{a^2 - u^2}+\frac{a^2}{2}\sin^{-1}\frac{u}{a} \right)'&=\frac{1}{2}\sqrt{a^2 - u^2}-\frac{u}{2}\frac{u}{\sqrt{a^2 - u^2}} +\frac{a^2}{2}\frac{1}{\sqrt{a^2 - u^2}}\\ &=\frac{1}{2}\sqrt{a^2 - u^2}+\frac{1}{2}\frac{a^2-u^2}{\sqrt{a^2 - u^2}}\\ &=\sqrt{a^2 - u^2}. \end{array}$$ Confirmed!
We replace $a$ with $R$ and $u$ with $x$ in the above formula and apply the Newton-Leibniz formula: $$\begin{array}{lllll} \frac{1}{2}\text{Area } &= \int_{-R}^R \sqrt{R^2 - x^2} \, dx \\ &=\frac{x}{2}\sqrt{R^2 - x^2}+\frac{R^2}{2}\sin^{-1}\frac{x}{R}\Bigg|_{-R}^R\\ &=\left( \frac{R}{2}\sqrt{R^2 - R^2}+\frac{R^2}{2}\sin^{-1}\frac{R}{R}\right) &-\left( \frac{-R}{2}\sqrt{R^2 - R^2}+\frac{R^2}{2}\sin^{-1}\frac{-R}{R}\right)\\ &=\frac{R^2}{2}\left( \sin^{-1}(1)+0-0-\sin^{-1}(-1) \right)\\ &=\frac{R^2}{2}\left( \pi/2-(-\pi/2) \right)\\ &=\pi \frac{R^2}{2}. \end{array}$$ $\square$
What if we can't find an integration formula for the function in question? There are always larger lists but it's possible that no book contains the function you need. In fact, we may have to create a new function just as we defined the Gauss error function as the integral: $$\operatorname{erf}(x)=\frac{2}{\sqrt{\pi}}\int e^{-x^2}\, dx.$$ Even if we keep adding these new functions to the list of “familiar” functions, there will always remain integrals not on the list.
The Fundamental Theorem is the culmination of our study of calculus, so far. The milestones of this study up to this point are outlined below: $$\begin{array}{r|l} \text{The Tangent Problem }&\text{The Area Problem}\quad\quad\\ \hline \quad \end{array}$$
$$\text{Approximations:}$$ $$\begin{array}{r|l} \quad\text{the difference quotient function}&\text{ the Riemann sum function }\quad\quad\\ \quad\text{the slopes of the secant lines on the graph}&\text{ the areas of the rectangles under the graph }\\ \frac{\Delta F}{\Delta x }&\sum_a^x f\, \Delta x \end{array}$$
With variable location, the limits of these approximations, as $\Delta x \to 0$, are the following: $$\begin{array}{r|l} \quad\\ \quad\text{the derivative function}&\text{ the indefinite integral}\quad\\ \hline \end{array}$$
According to the Fundamental Theorems, the operations of differentiation and integration cancel each other: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccccccc} \text{FTCI:}&f & \mapsto & \begin{array}{|c|}\hline\quad \int \square\,dx \quad \\ \hline\end{array} & \mapsto & F & \mapsto &\begin{array}{|c|}\hline\quad \frac{d}{dx}\square \quad \\ \hline\end{array} & \mapsto & f.\\ \text{FTCII:}&F & \mapsto & \begin{array}{|c|}\hline\quad \frac{d}{dx}\square \quad \\ \hline\end{array} & \mapsto & f & \mapsto &\begin{array}{|c|}\hline\quad \int \square\, dx\quad \\ \hline\end{array} & \mapsto & F+C. \end{array}$$
Warning: integration is a true function only an extra condition, such as $F(a)=0$, is imposed.