This site is being phased out.
Calculus 1: midterm 1
Midterm exam for Calculus 1: course
1. (a) Represent function $h(x)=\sqrt{x²-1}$, as a composition of two functions f and g, (b) Provide the formula for the composition $f(g(x))$ of $f(x)=x²+x$, and $g(x)=2x-1$.
2. Sketch the graphs of three functions with the three main types of discontinuities. Describe the discontinuities with limits.
3. (a) State the the $ɛ-δ$ definition of limit. (b) Use the definition to prove that $\lim _{x→0}\sqrt[3]{x}=0$.
4. Find the vertical asymptotes of the function $$f(x)=\frac{x-1}{(x²-1)(x+2)}$$ by computing necessary limits.
5. Evaluate the limit $$\lim _{x→∞}\frac{x³-1}{2x³-x+5}.$$ What is its graphical meaning?
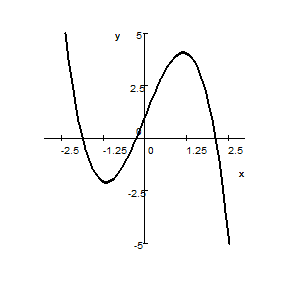
6. The graph of function f is given below. Sketch the graph of $$g(x)=2f(x+2)+3.$$ Explain how you get it.
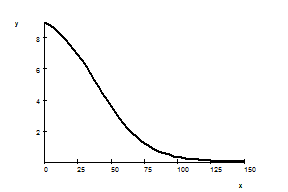
7. The pictured graph represents the altitude (in thousands of feet) of a plane above the ground at time $x$ (in sec). (a) What does the slope of the curve represent? (a) Describe what happened to the plane. Explain.
8. From the definition, compute the derivative of $f(x)=x²+1$ at $a=2$.
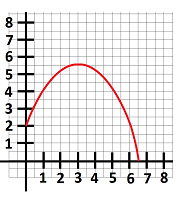
9. The graph of a function f(x) is given below. Estimate the values of the derivative $f'(x)$ for $x=0,4$, and $6$.
See next Calculus 1: midterm 1 solutions.