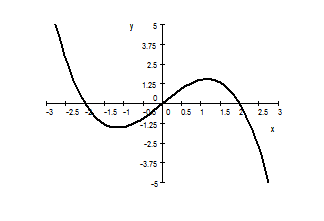This site is being phased out.
Calculus 1: test 1
This is a set of sample tests for Calculus 1: course.
1. (a) Finish the sentence: "Function $f$ is continuous at $x=a$ if ... " (the definition). (b) Use the definition in part (a) to prove/disprove that the function $f$ defined below is continuous at $a=0$ and $a=3.$ \[ f(x)=\left\{ \begin{align} {}% x+1 & \text{ if } x<0\\ x^{2}+1 & \text{ if } 0\leq x<3\\ 10 & \text{ if }x>3% \end{align} \ \right. . \]
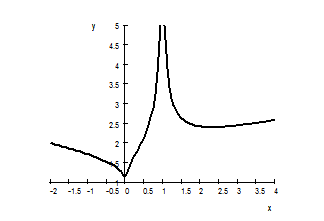
2. The graph of function $f$ is given below. (a) At what points is $f$ continuous? (b) At what points does the derivative of $f$ exist?
3. The graph of function $f$ is given below. Sketch the graph of $g(x)=2f(x-1)+2.$ Explain how you get it.
4. (a) Compute the derivative of $f(x)=3x^{2}-x$ at $a=1$ from the definition (i.e., as a limit). (b) Find the equation of the line tangent to the graph of $y=f(x)$ at the point corresponding to $a=1$.
5. Using the $\varepsilon-\delta$ definition of the limit, prove that $\lim\limits_{x\rightarrow1}(-x+1)=0.$
6. Find the vertical and horizontal asymptotes of the function and describe them as limits: \[ f(x)=\dfrac{2x^{2}}{x^{2}-1}. \]
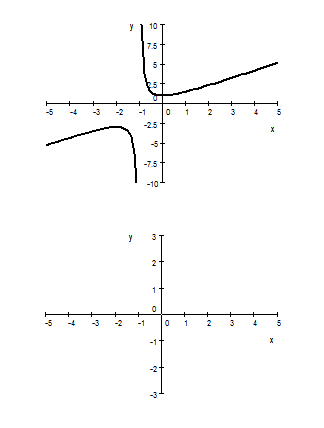
7. The graph of function $f$ is given below. Sketch the graph of the derivative $f^{\prime}(x)$ in the space under the graph of $f$. Identify all important features ($x$-intercepts, asymptotes etc) of your graph.