Derivative

Introduction

This is one of the motivations for differential calculus.

We want to study motion. Some questions we may ask are:

• On a winding road what is the direction of the headlights?
• Where does the rock go when released from the sling?

The answer is the tangents.

For the sling, we write

 f(x) = ( 1 - x2 )1/2

the graph of which is the circle. Then we differentiate and find the tangent line to the circle at any point:

 the slope of the tangent line is equal to the value of the derivative of f at the point. 

One is that strictly speaking the circle is given by

 f(x) = ±( 1 - x2 )1/2,

with ±.

Linear approximation

 Question: Given y = f(x), what is the best linear approximation of f around x = a?
 Answer: The tangent line,
 g(x) = f(a) + f'(a) ( x - a ).

Now we realize that the right term here is affine not linear.

Problem. Give the set of all "linear" (affine) functions passing through (a,f(a))

 g(x) = f(a) + m ( x - a ).

which one is he best approximation of f around x = a?

We know the answer:

 m = f'(x).

It's best but in what sense?

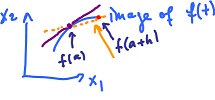
Let f: ℝ → ℝ, a ∈ ℝ. What is the rate of change of f? We have

 y: Change f(a + h) - f(a) - f(a)   the displacement 
 t: Change h                        the time passed

Then the rate of change of y with respect to t can be expressed as

 ( f(a + h) - f(a) ) / h.

Definition. Given f: ℝ → ℝⁿ, a ∈ ℝ, an affine function k: ℝ → ℝⁿ is the best affine approximation of f at x = a if

 (1) k(a) = f(a),
 (2) limt→a ( f(t) - h(t) ) / ( t - a) = 0.  

The last condition encodes the idea of approximation: not only the difference between f and its approximation is "small" but it's small even relative to the change in the input, t - a.

The theorem below justifies "the" in the definition.

Proposition. The best affine approximation is unique.

Proof Let k₁, k₂ satisfy (1) and (2). Then

 k1(t) = f(a) + v1(t - a)
 k2(t) = f(a) + v2(t - a).

Apply algebra along with (2) to conclude the proof.

Properties

Theorem (Mean Value Theorem). Let [ a, b ] ⊂ D(h), where h is differentiable on ( a, b ) and h is continuous on [ a, b ]. Then

 ( h(b) - h(a) ) / ( b - a ) = h′(c) for some c ∈ [ a, b ].

Corollary 1. Let

 f: ℝ → ℝ and
 f′(x) = 0, for all x in an interval I in ℝ. 

Then f is constant.

The condition implies that the derivative is zero, hence by the MVT, f is constant.

Another theorem that follows from the IVT is this.

Corollary 2. Let

 f′(x) = g′(x) for all x in an open subset U of ℝn and 
 f(a) = g(a). Then
 f(x) = g(x) for all x in U.

In order to proof the Corollary, take h = f - g, then apply Corollary 1.

Algebraic properties of the derivative

In this section we'll see how the derivative is affected by vector operations.

Addition and multiplication behave the exact same way as in dimension 1, but there is no division...

Consider f,g: ℝ → ℝⁿ and they have derivatives at a point x = a.

Sum rule.

 (f + g)' = f' + g'.

Proof. Coordinate-wise.

Product rule.

 (α f)' = α ⋅ f'.

Same proof as above.

Chain Rule. Let f: ℝ → ℝ, g: ℝ → ℝ, then fg: ℝ → ℝ if domain g ⊃ range f. If f′ and g′ exist, then

 (f ° g)′ = f′ ° g ⋅ g′.