Partial derivatives

${\bf R}^n$:

Given $z = f(u)$ at $u = a$, then

$$\begin{array}{} \frac{\partial f}{\partial x}_1(a) = \nabla_e f(a) {\rm \hspace{3pt} for \hspace{3pt}} e = ( 1, 0, ..., 0 ), \\ \vdots \\ \frac{\partial f}{\partial x}_n(a) = \nabla_e f(a) {\rm \hspace{3pt} for \hspace{3pt}} e = ( 0, 0, ..., 1 ), \end{array}$$

i.e., partial derivatives are particular cases of directional derivatives.

As it turns our we can turn this around and recover all directional derivatives.

Consider

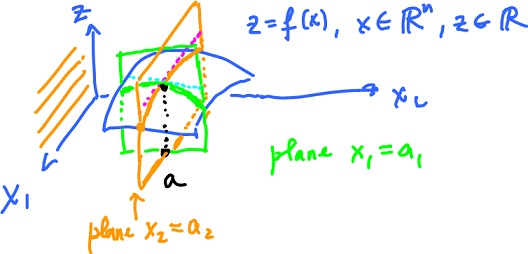
$$z = f(x), x \in {\bf R}^n, z \in {\bf R}, x = ( x_1 x_2 ), a = ( a_1 a_2 ).$$

(1) Cut the graph of $f$ with a plane parallel to the $x_1,z$-plane. The result is a curve

$$z = f ( x_1, a_2 ),$$

and the slope of the tangent line is $\frac{\partial f}{\partial x}_1(a)$, which is the derivative of $z = f ( \cdot, a_2 )$.

(2) Cut the graph of $f$ with a plane parallel to the $x_2,z$-plane. The result is a curve

$$z = f ( a_1, x_2 ),$$

and the slope of the tangent line is $\frac{\partial f}{\partial x_2}(a)$.

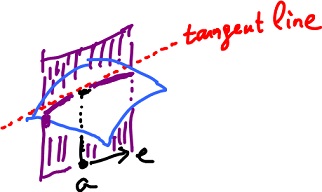
Let's compare to the directional derivative? The picture is very similar. The plane is spanned by $e$ and $( 0, 0, 1 )$. Cut a curve from the graph. Then

$$\nabla_e f(a)$$

is the slope of the curve at $x = a$.

Higher order partial derivatives are the derivatives of the partial derivatives:

$$\frac{\partial f}{\partial x_1}, \ldots, \frac{\partial f}{\partial x_n}$$

are functions from ${\bf R}^n \rightarrow {\bf R}$ and can also be differentiated with respect to $x_1, \ldots, x_n$ each.

From

$$\frac{\partial f}{\partial x_1}$$

we get $n$ second derivatives

$$\frac{\partial}{\partial x_k} (\frac{\partial f}{\partial x_1})$$

and so on. Altogether, we have $n^2$ second derivatives.

Frequently it's less though.

Example. Let $f( x, y ) = x^2 y$.

Then

$$\frac{\partial f}{\partial x} = 2xy, \frac{\partial f}{\partial y} = x^2,$$

$$\frac{\partial}{\partial y}( \frac{\partial f}{\partial x} ) = 2x, \frac{\partial}{\partial x}( \frac{\partial f}{\partial y}) = 2x.$$

Same!

These two are called mixed second derivatives.

The meaning of the others is clear. For example,

$\frac{\partial^2 f}{\partial x^2}$, is the concavity of $z = f( x, a^2 )$.

Analogously for $\frac{\partial^2 f}{\partial y^2}$.

Other notation for these is:

• $\frac{\partial^2 f}{\partial x \partial y}$
• $\frac{\partial^2f}{\partial x_1 \partial x_2}$
• $\frac{\partial^2 f}{\partial x_1^2}$
• $D_{1234}f$
• $f_{xy}$
• $f_{xx}$

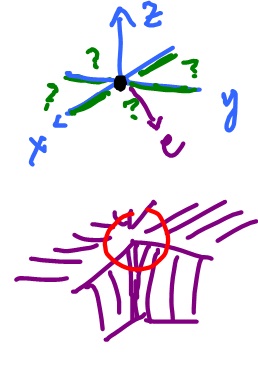
Example. It is possible that $\frac{\partial f}{\partial x}$ and $\frac{\partial f}{\partial y}$ exist, but some directional derivatives do not.

Consider the graph $z = f( x, y )$ with

$$f( 0, y ) = f( x, 0 ) = 0.$$

Then

$$\frac{\partial f}{\partial x} = \frac{\partial f}{\partial y} = 0 {\rm \hspace{3pt} at \hspace{3pt}} ( 0, 0 ),$$

and $\nabla_e f$ might not exist at $0$ because of the vertical drop. Specifically,

$$f( x, y ) = \frac{2xy^2}{x^2 + y^2} {\rm \hspace{3pt} if \hspace{3pt}} ( x, y ) \neq 0,$$

$$f( x, y ) = 0 {\rm \hspace{3pt} if \hspace{3pt}} ( x, y ) = 0.$$

Also, the vector made of the partial derivatives,

$$f' = \left( \frac{\partial f}{\partial x_1}, \ldots, \frac{\partial f}{\partial x_n} \right)$$

is the gradient..