Diffusion with various geometry

Outline

Recall that, naively, diffusion is modeled with Excel as follows: $$RC= RC -.25 *k*\bigg( \Big(RC-RC[-1]\Big) + \Big(RC-RC[1]\Big) + \Big(RC-R[-1]C\Big) + \Big(RC-R[1]C\Big) \bigg).$$

Here we will study diffusion on a grid with cells of various geometry.

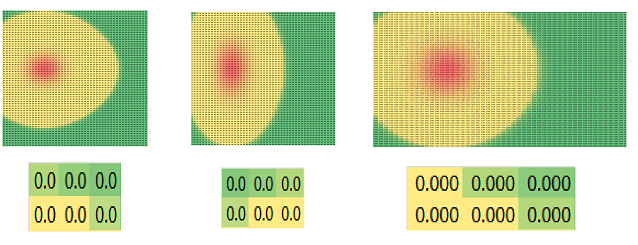
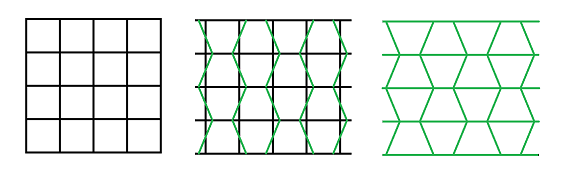
If we imagine that the horizontal walls are longer than the vertical ones, then one can change the coefficients of "vertical" differences in the above formula to capture that: $$RC= RC -.25 *k*\bigg( .5*\Big(RC-RC[-1]\Big) + .5*\Big(RC-RC[1]\Big) + 2*\Big(RC-R[-1]C\Big) + 2*\Big(RC-R[1]C\Big) \bigg).$$ As a result the material will spread faster in the vertical direction (second image) than normal (first image):

However if we stretch the cells in Excel horizontally (third image), the pattern becomes circular again!

On a deeper level, the geometry is supplied by Hodge duality and affects the forms that we deal with.

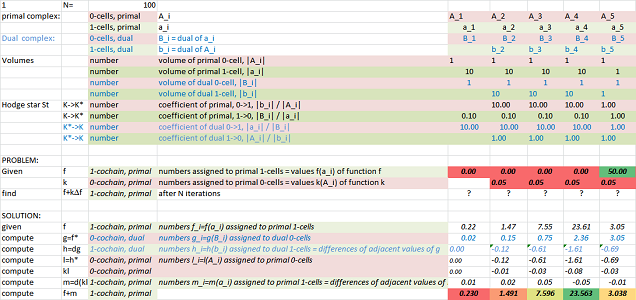
The Hodge star operator has been defined as a linear operator between the primal and the dual cochain complexes: $$\star = \star ^m:C^m(K)\rightarrow C^{n-m}(K^*).$$ Suppose the geometry is supplied by means of the $m$-dimensional volume $|b|$ of each $m$-cell $b$ -- in both primal and dual complexes. See geometric Hodge duality.

Now, given a primal $m$-cochain $\phi$ in the $n$-dimensional space, the discrete (geometric) Hodge star of $\phi$ is a cochain on the dual complex and it is defined by its values on the dual cells: for a $m$-chain $a$ and its dual $\star a$, we set $$\frac{1}{|\star a|}<\star \phi, \star a> = \frac{1}{|a|}<\phi, a>,$$ or equivalently $$\frac{1}{|a^*|} \phi ^*(a^*) = \frac{1}{|a|}\phi(a).$$ Therefore, the $m$th Hodge star is a diagonal matrix whose entries are the ratios of dual and primal volumes (up to a sign) in each dimension $m=0,1,...,n$: $$\star ^m_{ii}=\pm\frac{|a_i^*|}{|a_i|},$$

The idea is that the geometry is taken care of by the Hodge star and, therefore, we don't have to change anything about the diffusion equation: $$d_t U = d_x \star kd_x \star U.$$ Here $U$ is the amount of material and $k$ is a $(k-1,0)$-form that represents the permeability of each wall at a given time. As before, the right-hand side of the equation is given in this (non-commutative) diagram, if we start with $U$ in the right upper corner and make the full circle: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccc} & C ^{n-1}(K) & \ra{d} & C ^{n}(K) \\ & \da{\star} & \ne & \da{\star} \\ & C ^{1}(K^*)& \la{d} & C ^{0}(K^*)\\ \end{array} $$ with the multiplication by $k$ hidden in $C ^{0}(K^*)$. This time we can indicate the coefficients used as multiples: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccc} & C ^{n-1}(K) & \ra{d} & C ^{n}(K) \\ & \da{\times\frac{|b^{1}|}{|a^{n-1}|}} & & \da{\times\frac{|b^0|}{|a^n|}} \\ & C ^{1}(K^*)& \la{d} & C ^{0}(K^*),\\ \end{array} $$ where $a^m$ is a primary $m$-cell and $b^m$ is a dual $m$-cell.

Below we shall see how this formula for the star operator needs to be generalized...

Dimension 1

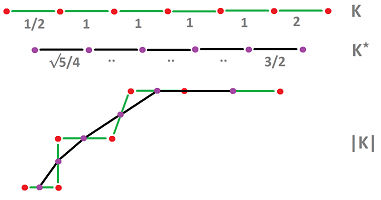
Let's consider diffusion for $1$-dimensional geometric cubical complexes such as this combination of primary and dual complexes:

From the last section, the diagonal elements of the Hodge start operator for dimension $n=1$ are: $$\star ^1_{ii}=\frac{|point|}{|edge|} = \frac{1}{length} = \frac{1}{|a_{i}|}.$$

In the diffusion equation, we have $\star ^1$ and $\star ^0$ in our diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccc} & C ^{0}(K) & \ra{d} & C ^{1}(K) \\ & \da{\times\frac{|b|}{1}} & & \da{\times\frac{1}{|a|}} \\ & C ^{1}(K^*)& \la{d} & C ^{0}(K^*),\\ \end{array} $$ where $a,b$ are primary and dual $1$-cells respectively.

It follows then that the right-hand side of our equation will have these coefficients (unlike in the "topological case" of diffusion): $$\frac{1}{|a|},$$ the length of the cell itself, and $$\frac{1}{|A^*|},\frac{1}{|B^*|},$$ the lengths of the $1$-cells dual to the end-points of $a$. The former give us: $$U(a)/|a|,$$ which is simply the density of the material inside $a$.

Conclusion. The amount of material $U$ exchanged by a primary $1$-cell $a$ with its neighbors is

• directly proportional to the difference of density in $a$ and those of its two neighbors, and
• inversely proportional to the lengths of the two pipes that leave $a$.

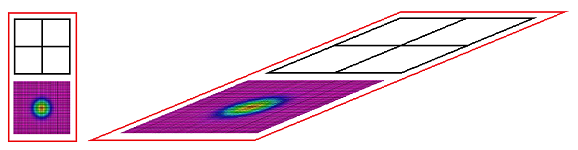
To confirm that these ideas make sense we run an Excel simulation below:

With a single spike in the middle, one can see how the smaller cells on the right , $$|a_5|=|a_6|=|a_7|=|a_8|=|a_9|=1,$$ quickly become uniform but the larger ones on the left, $$|a_1|=|a_2|=|a_3|=|a_4|=10,$$ develop slower.

Source file: diffusion_dim_1_w_geometry.xlsx

Exercise. Find the speed of propagation as a function of the length of the cell.

Exercise. Suppose we have two rods made of two kinds of metal soldered together. The cells will expand at two different rates when heated. Can we see changing of its geometry? Model and illustrate with Excel. Hint: in order to keep this $1$-dimensional, consider a single rod and then simply compare the geometry to the heated rod and that of the original rod.

Dimension 2, square vs rectangular grids

We have the following diagonal entries in the case of a rectangular grid and dimension $n=2$: $$\star ^2_{ii}=\frac{|point|}{|rectangle|} = \frac{1}{area} = \frac{1}{\Delta x \Delta y},$$ $$\star ^1_{ii}=\frac{|edge|}{|edge|} = \frac{length}{length} = \frac{\Delta y}{\Delta x }.$$

In the diffusion equation, we have $\star ^2$ and $\star ^1$ in our diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccc} & C ^{1}(K) & \ra{d} & C ^{2}(K) \\ & \da{\times\frac{|b|}{|a|}} & & \da{\times\frac{1}{|\sigma|}} \\ & C ^{1}(K^*)& \la{d} & C ^{0}(K^*),\\ \end{array} $$ where $a,b$ are primary and dual $1$-cells respectively and $\sigma$ is a $2$-cell.

It follows then that its right-hand side of our equation will have these coefficients: $$\frac{1}{|\sigma|},$$ the area of the cell itself, and $$\frac{|a|}{|a^*|},...$$ the length of the $1$-cell over the length of its dual. Again we observe that $U(\sigma)/|\sigma|$ is the density inside $\sigma$.

Conclusion. The amount of material $U$ exchanged by a primary $2$-cell $\sigma$ with its neighbors is

• directly proportional to the difference of density in $\sigma$ and those of its neighbors,
• inversely proportional to the lengths of the pipes that leave $\sigma$, and
• directly proportional to the thickness of these pipes.

To illustrate the last point, let's consider our grid:

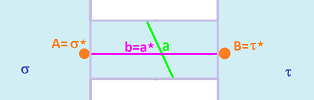
If we use the $2\times 1$ grid, we have the following lengths of $1$-cells:

• horizontal primary $|a|=2$ and its dual $|a^*|=1$;
• vertical primary $|a|=1$ and its dual $|a^*|=2$.

Then the Excel formula is the same as the one discussed above: $$RC= RC -.0025*\bigg( .5*\Big(RC-RC[-1]\Big) + .5*\Big(RC-RC[1]\Big) + 2*\Big(RC-R[-1]C\Big) + 2*\Big(RC-R[1]C\Big) \bigg).$$ and, with a single source, it produces a circular pattern, as expected:

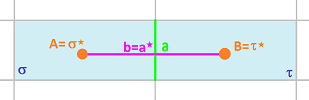
So, the material flows left to right through what appears to be a pipe of length $|a^*|$ and width $|a|$:

Non-rectangular grid

What if the wall is sloped? Does it affect the amount of material that crosses to the other room?

If we assume that the liquid flows along the line (the pipe $a^*$) that connects the centers of the rooms, then what matters is the cross-section of the pipe.

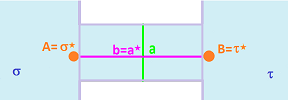
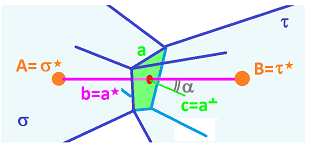
Let's consider the general case of cells of irregular shape, still in dimension $2$:

The cross section is equal to length of the projection of $a$ on the normal of $|a^*|$: $$|a|\sin \varphi,$$ where $\varphi$ is the angle between $a$ and $a^*$.

So, the coefficient in the diffusion equation should be $$\frac{|a|\sin \varphi }{|a^*|}.$$

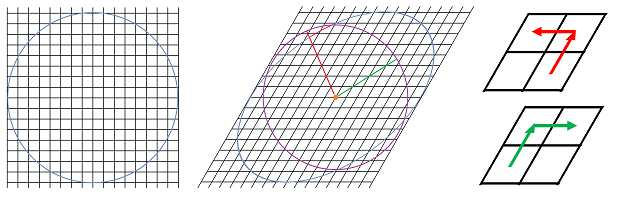
Consider this trapezoid grid:

It is made from a square grid by turning the vertical edges by the same angle alternating left and right.

Exercise. Test the new, generalized formula for diffusion of a single source on this grid. Does it produce a isotropic, circular pattern?

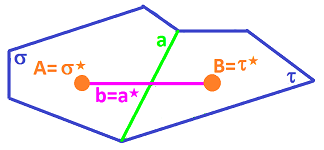
Consider now the rhomboid grid:

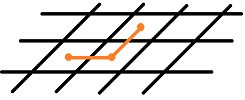
The flow in any of the four directions on the grid is the same, just as on the square grid but slower (measured in cells -- more walls per unit of length, hence $\cos \alpha$). Therefore, a single source diffusion will produce a skewed, non-circular pattern:

The resulting anisotropy is explained by the anisotropy of the set up. Below, the red and green segments are equal in length, but it follow the red one on would have to cross 9 walls vs only 4 for the green:

See also Convergence of the discrete to the continuous.

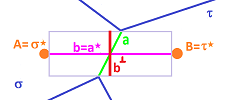
An alternative approach anticipates the general case: $n$-dimensional rooms, $\sigma$, with $(n-1)$-dimensional walls, $a$, but still $1$-dimensional pipes, $a^*$. We use the fact that the amount of liquid that crosses the surface is proportional to:

• the component of the flow orthogonal to the surface, i.e., $\cos \alpha$, where $\alpha$ is the angle between $a^*$ and the normal $a^⊥$ to $a$; and
• the area of the this part of the surface, i.e., $|a|$.

Conclusion. The amount of material $U$ exchanged by a primary $2$-cell $\sigma$ with its neighbors is

• directly proportional to the difference of density $U(\sigma)/|\sigma|$ in $\sigma$ and those of its neighbors, $\star\partial\partial ^{-1}\star\sigma$,
• inversely proportional to the lengths of the pipes that leave $\sigma$, $\star\partial \sigma$,
• directly proportional to the cross-sections of these pipes, $\star\partial \sigma$ (or areas of the walls of $\sigma$, $\partial \sigma$), and
• directly proportional to the cosine of the angle between these pipes and these walls.

So, our coefficient is $$\frac{|a|\cos \alpha}{|a^*|}.$$ Since $\alpha + \varphi =\pi /2$, it's equal to the one above.

Hodge star operator and metric tensor

Recall, a discrete metric tensor on a cubical complex $K$ as a function that associates a number to each location, i.e., a vertex $A$ in $K$, and each pair of directions at that location, i.e., edges $x=AB,y=AC$ adjacent to $A$: $$(A,AB,AC) \mapsto < AB, AC >(A) \in {\bf R}.$$ It is a function: $$<\cdot,\cdot>(\cdot): T(K) \rightarrow {\bf R},$$ the domain $T(K)$ of which is the discrete tangent bundle.

Clearly, it's not general enough.

We extend, first, the definition of metric tensor to include not only the inner products of (and the angles between) adjacent primary edges but also of adjacent dual edges. This way we have two functions: $$<\cdot,\cdot>(\cdot): T(K) \rightarrow {\bf R},$$ $$<\cdot,\cdot>(\cdot): T(K^*) \rightarrow {\bf R}.$$

Further, we extend the metric tensor to include the inner product of an edge and its dual: $$<a^*, a>.$$ The product is realized as the inner product of vector $a^*$ and the normal vector $a^⊥$ to $a$ with the same length: $$<a^*, a^⊥>,$$ $$|a^⊥|=|a|.$$

Then, for the diffusion equation analyzed above, we have $$\cos \alpha = \frac{<a^*, a>}{|a^*||a|}.$$ Therefore, the coefficient is $$\frac{<a^*, a>}{|a^*|^2}.$$

We have realized that the formula for the Hodge star operator that we have used is only applicable to rectangular grids. Therefore, the Hodge star $\star ^m$ of degree $m=n-1$ is a diagonal matrix whose $i$-th entry is the ratio of the dual volume and the projection of the primal volume, instead of just "the ratio of the dual and primal volume". More precisely, it is $$\star ^m_{ii}=\pm\frac{|a^*_i|^2}{<a_i^*, a_i>}.$$

Note: As far as the realization of this geometric complex is concerned, the placement of the centers of the cells varies. One of the most common choices is that of the Voronoi diagram.