Geometric Hodge duality

Dual complex

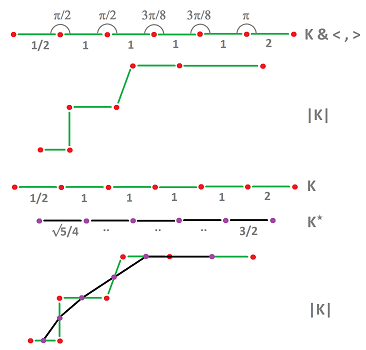
Suppose we assume that the lengths of the cells are given, to make sense of concavity we still need the construction to be rigid. We start by thinking of $1$-cells as rods and $0$-cells as hinges. There are two ways to make the angles of the hinges fixed.

First, we can simply specify the angles between the rods. Mathematically, this is an inner product which leads to the idea of metric tensor.

Second, we can connect the centers of the adjacent rods using an extra set of rods. This leads to the idea of a geometric Hodge duality.

Second derivative and Hodge duality

The concavity of a function is determined by the sign of the second derivative, which is "the rate of change of the rate of change". It can be defined as a single limit: $$g' '(u)=\lim_{h\to 0}\frac{\frac{g(u+h)-g(u)}{h} - \frac{g(u)-g(u-h)}{h}}{h}.$$

This is what we have in the discrete case:

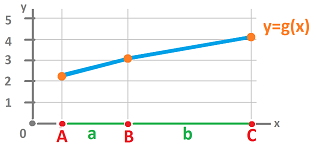
The discrete analogue of the second derivative above is $$\frac{\frac{g(C)-g(B)}{|C-B|} - \frac{g(B)-g(A)}{|B-A|}}{|C-A|/2}.$$

Let's take a closer look at this formula.

The numerators are easily recognized as the exterior derivative of the $0$-form $g$ evaluated at the $1$-cells $a$ and $b$ respectively.

Meanwhile, the denominators in the upper part are the lengths of these cells, which will be denoted by $|a|$ and $|b|$.

What about the bottom?

Using the idea of dual complex, which happens to be flat here, we define the second derivative (not to be confused with $dd$) as $$g' '(B)=\frac{\frac{dg(b)}{|b|} - \frac{dg(a)}{|a|}}{|B^*|},$$ where $B^*$ is the "dual cell", the extra rod, of the vertex $B$.

We have also defined the second derivative via "topological" Hodge duality. Consider this Hodge duality diagram, where $\star$ stands for Hodge duality of differential forms: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccc} &C^{0}(K)& \ra{d} & C^1(K) &\\ &\ua{\star} & \ne & \da{\star} & \\ &C^{1}(K^*)& \la{d} & C^{0}(K^*)& \\ \end{array} $$ Then the second derivative above is the result of going around the leftmost square: $$g' '(B)= \star d \star dg (B).$$

The two formulas match -- except for the coefficients equal to the reciprocals of the lengths of these edges. Indeed,

• first $\star$ is applied to a $1$-form defined on edges $a,b$ there is division by the lengths of these edges; and
• second $\star$ is applied to (dual) $1$-form defined on edge $B^*$ there is division by the length of this edge.

In other words, the formula is:$$g' '= \Big(\frac{1}{|\cdot|}\star\Big) d \Big(\frac{1}{|\cdot|}\star\Big) dg .$$ The comparison suggests that in order to introduce geometry via Hodge duality, these coefficients should be inserted into the matrix of the Hodge star operator. Since its matrix is diagonal with only $\pm 1$ on the diagoanl, it's easy.

$$\star _{ii}=\frac{\pm 1}{|a_i|},$$ where $a_i$ is the $i$th $1$-cell in the complex.

Hodge star

The Hodge star operator has been defined as a linear operator between the primal and the dual cochain complexes: $$\star = \star ^k:C^k(K)\rightarrow C^{n-k}(K^*).$$

Suppose the geometry is supplied my means of the $k$-dimensional volume $|b|$ of each $k$-cell $b$ -- in both primal and dual complexes. The idea implies:

• for $k=1$, $|b|=$ the length of $b$;
• for $k=2$, $|b|=$ the area of $b$;
• for $k=3$, $|b|=$ the volume of $b$;
• etc

However, abstractly these are simply positive numbers assigned to each cell, and

• for $k=0$, $|b|=1$.

Now, given a primal $k$-cochain $\phi$ in the $n$-dimensional space, the discrete (geometric) Hodge star of $\phi$ (denoted by $\star \phi$ or $\phi ^*$) is defined as follows. It is a cochain on the dual complex and it is defined by its values on the dual cells: for a $k$-chain $a$ and its dual $\star a$, we set $$\frac{1}{|\star a|}<\star \phi, \star a> = \frac{1}{|a|}<\phi, a>,$$ or equivalently $$\frac{1}{|a^*|} \phi ^*(a^*) = \frac{1}{|a|}\phi(a).$$

Therefore, the $k$th Hodge star is a diagonal matrix whose entries are the ratios of dual and primal volumes (up to a sign) in each dimension $k=0,1,...,n$: $$\star ^k_{ii}=\pm\frac{|a_i^*|}{|a_i|},$$ where $a_i$ is the $i$th $k$-cell in the complex.

In particular, for dimension $n=1$: $$\star ^1_{ii}=\frac{|point|}{|edge|} = \frac{1}{length} = \frac{1}{\Delta x}.$$

We have the following diagonal entries in the case of a rectangular grid and dimension $n=2$: $$\star ^2_{ii}=\frac{|point|}{|rectangle|} = \frac{1}{area} = \frac{1}{\Delta x \Delta y},$$ $$\star ^1_{ii}=\frac{|edge|}{|edge|} = \frac{length}{length} = \frac{\Delta y}{\Delta x }.$$

An important property of Hodge star is that for a $k$-form $\alpha$, $$\star \star \alpha = (-1)^{k(n-k)} \alpha.$$

We test these ideas by considering diffusion with various geometry.