This site is being phased out.
Linear operator
A linear function preserves vector operations:
- scalar multiplication: $f(ax) = ax$, and
- addition: $f(x + y) = f(x) + f(y)$.
A linear operator is determined by its values on the elements of the basis of the domains space, as they are expressed as linear combinations of the elements of the basis of the target space. The coefficients of these linear combinations form the columns of the matrix of linear operator.
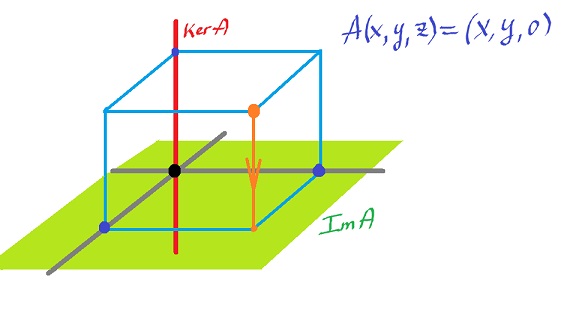
Kernel of projection:
Theorem 1. If $M, L$ are vector spaces and $A: M → L$ is a linear operator, then $$M / \it{ker} A ≌ \it{im} A.$$
See kernel of linear operator (and image).
Theorem 2. If Y is a subspace of vector space X, then $$\it{dim} X / Y = \it{dim}X - \it{dim}Y.$$