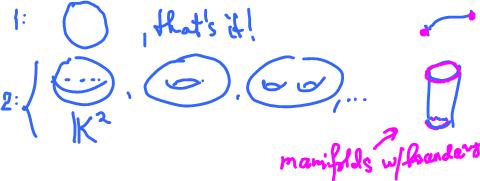Surfaces and their homology

Definition and examples

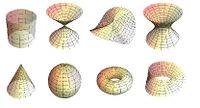
Well known examples of surfaces are:

• the plane,
• the paraboloid,
• the cylinder,
• the sphere,
• the torus,
• the Klein bottle,
• the projective plane.

What do they have in common? Locally, they look like disks. Just like the Earth looks like a plane if you don't move far.

Since disks are homeomorphic to the plane which is the $2$-dimensional Euclidean space ${\bf R}^2$, we can say that surfaces are "locally Euclidean".

Thus surfaces are $2$-dimensional manifolds.

Definition. A topological space $S$ is called a surface (without boundary) if $S$ is Hausdorff and every point in $S$ has a neighborhood homeomorphic to ${\bf R}^2$.

Exercise. One of the surfaces depicted above isn't, which one? Consider also something that looks like a book?

Theorem. The disjoint union of two surfaces is a surface.

Because of this theorem we concentrate on path-connected surfaces. We will also concentrate only on compact surfaces, since non-compact surfaces can't be represented as finite cell complexes.

While there is only one compact connected $1$-manifold, there is a variety of surfaces.

Clearly, there are many "surfaces" that aren't $2$-manifolds as defined:

• the closed disk,
• any of the surfaces listed at the top with holes punched through,
• the cylinder,
• the Mobius band.

The difference is that these surfaces have "edges" aka boundaries.

Definition. A topological space $S$ is called a surface with boundary, if $S$ is Hausdorff and every point in $S$ has a neighborhood homeomorphic to:

• either the whole $2$-dimensional Euclidean space ${\bf R}^2$
• or the half-space $\{x \in {\bf R}^2 \colon x_1 \geq 0 \}$.

(In other words, these are disks and half-disks.) The latter points form the boundary of the surface.

For more examples, see Quotients of manifolds.

A surface is called non-orientable is it contains the Mobius band:

• Mobius band, Klein bottle, projective plane, etc.

The rest are orientable:

• sphere, torus, etc.

Punching holes in a surface without boundary will create a variety of surfaces with boundary:

The boundaries of the holes are circles, hence the boundary of these surfaces are too. Are all surfaces with boundary like that?

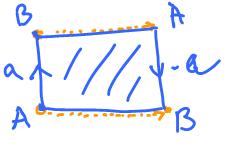
Consider the Mobius band. You travel along the "lower edge" from $A$ to $B$, and next you are at $B$ on the "upper" edge, the you travel along it to $A$. You come back where you started. So, indeed, the boundary of the Mobius band is homeomorphic to the circle.

Theorem. The boundary of a compact surface $S$ is

• a closed subset of $S$,
• a compact $1$-manifold without boundary,
• the union of a finite number of circles.

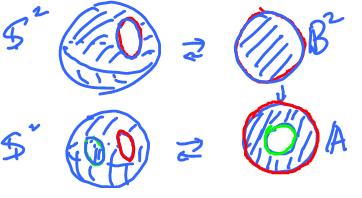
It follows that a surface with boundary can be easily turned into a surface without boundary by attaching a few disks:

Exercise. What happens if you attach the disk to the boundary of the Mobius band? Prove via a diagram. Solution:

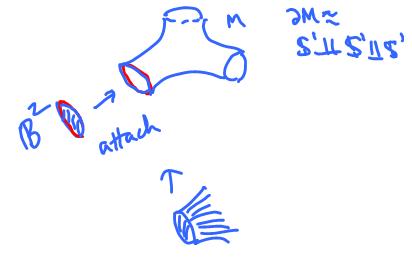
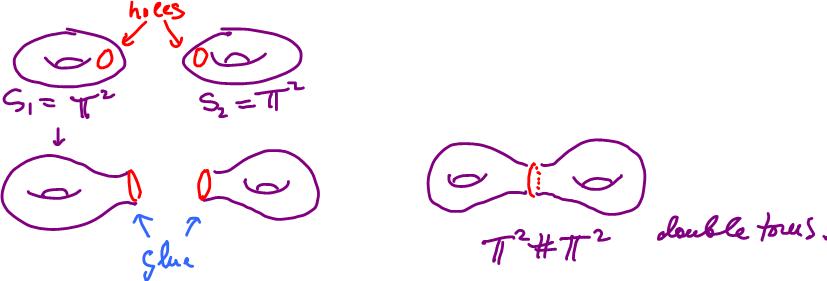
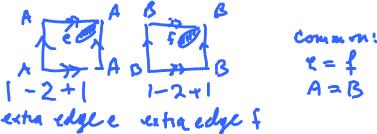
Further, any two surfaces can be attached to each other by punching holes in them and then gluing them together along these edges. For example, this is how you create the double torus by attaching two tori to each other in this fashion.

This construction is called the connected sum $S_1 \# S_2$ of surfaces $S_1, S_2$.

Theorem (Classification of surfaces). (1) A compact connected surface is homeomorphic to

• the sphere, or
• the connected sum of of $n$ tori, or
• the connected sum of of $n$ projective planes.

(2) These options are not homeomorphic.

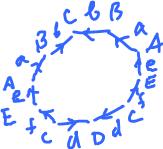
Every surface (without boundary) can be represented as polygon with the edges glued together as in this diagram:

Every edge has to appear twice (why?). What about vertices?

Exercise. Cut a hole in the middle of the projective plane and represent the result as a cell complex with a single $2$-cell (standard diagram for surfaces). What is it? Solution:

Triangulations of surfaces

Recall that every point in a surface (without boundary) has a neighborhood homeomorphic to ${\bf R}^2$.

Suppose we have a $2$-dimensional simplicial complex $K$. How do we know that the realization of $K$ is a surface?

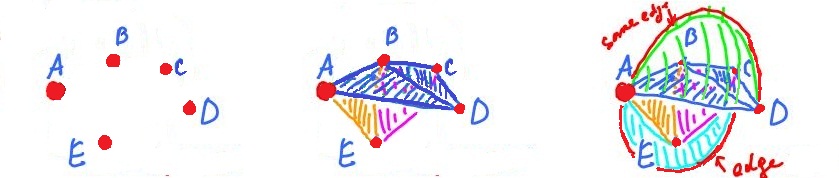
For example, consider of the complex $$ABD, BCD, ACD, ABE, BCE, ACE.$$ If we start attaching cells to each other:

we discover that its realization is homeomorphic to the sphere.

Can we answer the question by examining the list of simplices? The answer is Yes.

The first requirement a complex has to satisfy to be a surface is:

• (a) each edge is shared by exactly two faces.

This condition can fail in two ways:

1. an edge is contained in exactly one face,
2. an edge is shared by more than two faces.

In the first case we have, possibly, a surface with boundary. In the second, a point on this edge does not have a neighborhood homeomorphic to the disk.

Now, how do we restate this condition combinatorially for a given simplicial complex $K$ given by a list of subsets of ${A,B,C,...}$?

In terms of sets, every face is a triple, such as $ABC$, and every edge is a double, such as $AB$. Condition (a) can then be restated in term of subsets of ${A,B,C,...}$ as:

• (A) if $AB∈K$ then there are exactly two $C,D∈K$ satisfying

$$ABC, ABD∈K.$$

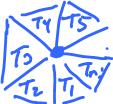
This condition does not guarantee that the realization of $K$ is a surface, as the image below shows.

Indeed, condition (A) is satisfied here but the vertex in the middle does not have a neighborhood homeomorphic to the disk.

Then, we have to require that the faces around each vertex are arranged in a circular fashion to form a disk-like surface.

Given a vertex $A$ the faces (triangles) that contain $A$ have to form a "cycle":

$T_0$ glued to $T_1$ glued to $T_2$ ... $T_n$ glued to $T_0$.

We can state this as a condition on faces:

• (b) for each vertex $A$, if
  • all edges that contain $A$ are $E_0, E_1, ..., E_n$ and
  • all triangles that contain $A$ are $T_0, T_1, ..., T_n$,
• then they can be re-indexed in such a way that:
  • $E_0$ is shared by $T_0, T_1$;
  • $E_2$ is shared by $T_1, T_2$;
  • ...
  • $E_n$ is shared by $T_n, T_0$.

Note: This collection of simplices is called the star of vertex $A$. For a related construction see Nerve of cover.

Restated in terms of subsets of ${A, B, C, ...}$, condition (b) will take the following form:

• (B) for each $A∈K$, the set ${B∈K: AB∈K}$ can be represented as ${B_0, B_1, ..., B_n}$ with

$$AB_0B_1, AB_1B_2, ..., AB_nB_0∈K.$$

Theorem. If a simplicial complex $K$ satisfies conditions (A) and (B) then its realization $|K|$ is a surface.

Orientable surfaces

A surface is called non-orientable if it contains the Mobius band:

• Mobius band,
• Klein bottle,
• projective plane, etc.

The rest are orientable:

• sphere,
• cylinder,
• torus, etc.

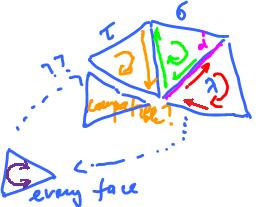
Definition. The orientations of two faces that share an edge are called compatible provided they induce the opposite orientations on the edge.

We can choose these orientations, if we deal with one edge at a time.

Can we ensure that all pairs of faces have compatible orientations?

We might proceed as follows. Start with $\sigma$ and $\tau$ compatibly oriented. Then, suppose ${\sigma}$ has another edge $d$ shared with face $\lambda$. Then $\lambda$ has to have the compatible orientation with ${\tau}$. Next, $\lambda$ has an edge $f$ shared with another face which has to have the compatible orientation with ${\tau}$, etc. At every step we move from a face to an adjacent face and every time the orientation of the next face is "forced". This may continue for a while. But what happens if we make a full circle and come back to ${\tau}$? It's possible that the orientation we want to impose on ${\tau}$ will be opposite of what we have already.

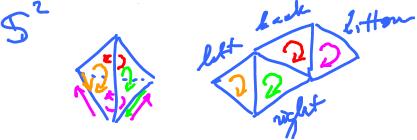
To sort this out, consider these two examples: triangulated sphere:

and Mobius band:

Is there a compatible orientation of the whole thing? Start with ${\tau}$, oriented clockwise. We orient ${\sigma}$ compatibly (generates opposite orientation on the edge they share) etc. For the Mobius band we have a problem:

• ${\tau}$ orients $a$ as $a$.
• ${\mu}$ orients $a$ as $a$.

They are not opposite! Therefore this is not a compatible orientation of ${\bf M}$.

Exercise. Show that there is no compatible orientation of the Mobius band, regardless of the triangulation.

Corollary. A non-orientate surface (contains ${\bf M}$) can't be compatibly oriented.

See also Orientable manifolds.

Theorem. Orientability is a topological invariant.

Euler characteristic of surfaces

The Euler characteristic $\chi(K)$ of $n$-dimensional cell complex $K$ is defined as the alternating sum of the number of cells in $K$ for each dimension:

$\chi(K) = \# 0$-cells $- \# 1$-cells $+ \# 2$-cells $- ... \pm \# n$-cells.

In case of surfaces, this is simply: $$\begin{array}{} \chi(K) &= \# 0{\rm -cells \hspace{3pt}} - \# 1{\rm -cells \hspace{3pt}} + \# 2{\rm -cells \hspace{3pt}} \\ &= \# {\rm \hspace{3pt} vertices} - \# {\rm \hspace{3pt} edges} + \# {\rm \hspace{3pt} faces}. \end{array}$$

Exercise. Compute the Euler characteristic of

• the Klein bottle,
• the $n$-torus.

Theorem. The Euler characteristic is a topological invariant, i.e., if surfaces $S$ and $T$ are homeomorphic, then $\chi(S) = \chi(T)$.

The converse of this theorem is not true, i.e., the Euler characteristic is not a complete topological invariant. Indeed there are non-homeomorphic complexes with the same Euler characteristic. Find examples (Exercise).

To justify this theorem, consider what elementary subdivisions of a $2$-dimensional cell complex do to the Euler characteristic:

Exercise. Show that if $S'$ is the barycentric subdivision of $S$ then $$\chi(S') = \chi(S).$$

Let's consider what happens to the Euler characteristic when we form the connected sum of two tori.

Cutting the disks out has the following consequences:

• no new faces, net effect $0$,
• one new, shared edge, net effect $-1$,
• one existing vertex becomes shared, net effect $-1$.

Thus, the net effect is $-2$.

This argument applies to all surfaces:

Theorem. For two surfaces $S$ and $T$, $$\chi(S \# T) = \chi(S) + \chi(T) - 2.$$

Exercise. Use the formula to compute the Euler characteristic of the $n$-torus.

For more see also Euler-Poincare formula.

Homology of surfaces

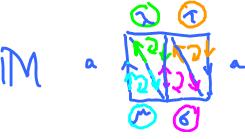
Suppose $M$ is a surface, without boundary, path-connected, and compact (finitely many cells).

What do we know about the homology of $M$?

The $0$th homology $H_0$ is simple: $$H_0(M) = {\bf R}.$$

What about $H_1$? It varies:

$H_1($${\bf S}^2$) $= 0$,

$H_1($${\bf T}^2$) $= H_1($${\bf K}^2$) $= {\bf R}^2$,

$H_1({\bf T}^2$$\#$${\bf T}^2) = {\bf R}^3$, etc.

Turns out $H_2$ does not vary as much:

$H_2($${\bf S}^2$) $= H_2$(${\bf T}^2$) $= {\bf R}$,
$H_2($${\bf K}^2$) $= 0$.

Whether it's ${\bf R}$ or $0$ is determined by the orientability of the surface. Essentially, orientability tells us whether $M$ holds air.

As a surface $M$ has no $3$-cells, its $2$-boundary group is trivial: $$B_2(M) = \partial (C_3(M)) = \partial(0) = 0,$$ where $\partial$ is the boundary operator. Therefore, we only need to compute the $2$-cycle group: $$H_2(M) = Z_2(M) / B_2(M) = Z_2(M) / 0 = Z_2(M).$$

Suppose $C$ is a non-zero $2$-cycle and $$C = \displaystyle\sum_s d_s s, d_s \in {\bf R},$$ with summation over all faces $s$ in $M$, with some coefficients $d_s = 0$, possibly. Since $C$ is a cycle, the boundary $\partial C$ of $C$ is zero: $$\partial C = 0, {\rm \hspace{3pt} or}$$ $$\partial C = \displaystyle\sum_s d_s \partial s = 0.$$

Since $\partial C$ consists of $1$-cells, let's take a look at the edges of $M$. Recall that in a surface, every edge is shared by exactly two faces ($2$-cells).

Therefore, every edge $e$ appears exactly twice in the above sum. Since $\partial \tau = 0$, every edge $e$ has to cancel. Hence

Lemma $1$. If edge $e$ is shared by faces $\sigma$ and $\tau$ then $$d_{\sigma} = \pm d_{\tau}.$$

Taking into account that $C$ is non-zero, there is a face $s$ with $d_s \neq 0$.

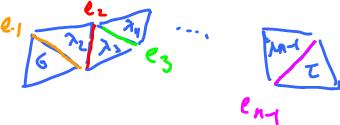
Since $M$ is connected, one can get from $s$ to any other face by following edge-face-edge-face... sequence:

By applying Lemma $1$ inductively, we obtain

Lemma. For any two faces $\sigma$ and $\tau$ in $M$, $$d_{\sigma} = \pm d_{\tau}.$$

Which sign? We have to look at the orientations of these faces.

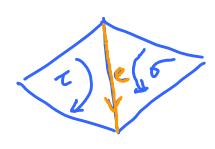
For example, suppose $$C = \sigma + \tau + {\rm \hspace{3pt} terms \hspace{3pt} w/o \hspace{3pt}} \sigma, \tau$$ with orientation given here:

Then $$\begin{array}{l} \partial C &= e + e + {\rm \hspace{3pt} terms \hspace{3pt} w/o \hspace{3pt}} e \\ &\neq 0, \end{array}$$ because $e \neq 0$. Even if the orientation of $e$ is chosen opposite of this, the result is the same. Its orientation does not matter; what matters is the way $\sigma, \tau$ appear in $C$ (recall that the homology of a cell complex is independent of the orientations of its cells). Of course we could choose $$C = \sigma - \tau + \ldots,$$

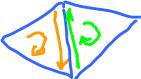
which will cancel $e$, with these orientations. This answer, however is unsatisfactory because, what about the rest of the edges?

It's hard to enforce canceling by having opposite signs in the decomposition of $C$. It's easier to have the same signs for $\sigma$ and $\tau$ and then ensure cancellation by choosing appropriate orientations. Indeed, if we reverse the orientation of $\tau, e$ is canceled: $$\begin{array}{l} \partial C &= \partial ( \sigma + \tau + {\rm \hspace{3pt} terms \hspace{3pt} w/o \hspace{3pt}} \sigma, \tau ) \\ &= e - e + {\rm \hspace{3pt} terms \hspace{3pt} w/o \hspace{3pt}} e \\ &= {\rm \hspace{3pt} terms \hspace{3pt} w/o \hspace{3pt}} e. \end{array}$$

To keep track of all faces and edges and ensure canceling, we introduce this terminology. The orientations of two faces that share an edge will be called compatible if they induce the opposite orientations on the edge.

We can choose these orientations, if we deal with one edge at a time. But can we ensure that all pairs of faces have compatible orientations?

From what we know about orientable surfaces (they don't contain the Mobius band),

Theorem. A surface can be compatibly oriented iff it's orientable.

It follows

Corollary. Suppose $C$ is a non-zero $2$-cycle in an orientable connected surface $M$ and $$C = \displaystyle\sum_s d_s s, d_s \in {\bf R},$$ over all faces $s$ in $M$. Then for any two faces $\sigma$ and $\tau$ in $M$ $$d_{\sigma} = d_{\tau}.$$

From the corollary, it follows that $$C = d \displaystyle\sum_s s,$$ for some real $d$. It follows,

Theorem. For an orientable connected compact surface $M$ without boundary, the second homology group is generated by the sum of all faces in $M$: $$H_2(M) = {\bf R} = {\rm span}\{\displaystyle\sum_s s \}.$$

This generator is called the fundamental class of the surface.

Exercise. What if $M$ had boundary?

Theorem. For a non-orientable connected compact surface $M$ without boundary, $$H_2(M) = 0.$$

Exercise. Prove the theorem. Hint: the construction is the same as above: propagation of coefficients of faces in the decomposition of $C$.