Chains vs cochains

Redirect to:

• Differential forms

Confusion is common here, especially in the context of discrete exterior calculus.

It is common for a student to speak of discrete differential forms of degree $1$ as linear combinations of directed edges or, more generally, oriented cells. However, the latter are chains and the former are cochains.

It is tempting because they "look" very much the same. Frequently one just assigns numbers to cell in a complex.

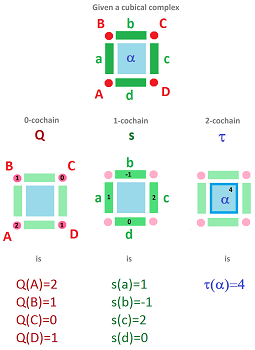
To see the difference, observe that the numbers aren't the coefficients of the cells in some chain but the values of the 1-cochain on these cells:

In the diagram,

• the names of the cells are given in the first row,
• the values of the form on these cells are given in the second row, and
• the algebra is in the third, with the formulas written over the complex for convenience.

The second row gives you the compact representation of the form without naming the cells.

Algebraically:

• both chains and cochains are formal linear combinations of some abstract geometric objects;
• the algebra is exactly the same: addition and scalar multiplication;
• they form vector spaces of the same dimension -- they are dual spaces!

Cochains are real-valued, linear functions defined on chains:

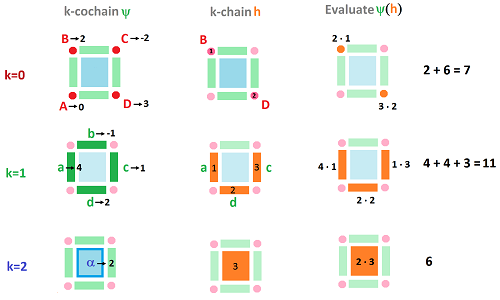
Here we have:

• a $1$-chain $h=3d+2a+(-1)e+0f$,
• a $1$-cochain $\psi$ given by: $\psi (a)=-1,\psi(b)=1$ etc;

then we evaluate $\psi$ on $h$ one cell at a time:

• $\psi (h)=0\cdot 3+ 1\cdot 2 + 2\cdot (-1) +3\cdot 0=0.$

One should recognize this as a line integral: $$\psi (h)=\int _h \psi .$$

The differences become major when we look at these spaces.

The vector space of all $k$-chains is $C_k.$ Meanwhile, the space of all $k$-cochains is $C^k.$

The basis of the $k$-chains, $C_k$, is the $k$-cells, say,

• $\gamma = \{c_1,...,c_n\}$,

while the basis of cochains, $C^k$, is

• $\gamma^* = \{f_1,...,f_n\}$.

It is defined, following the duality, on the basis $\gamma$, by $$f_i(c_j)=\delta_{ij}.$$

So these spaces are isomorphic in every dimension: $$C_k \simeq C^k.$$ but not as "graded vector spaces".

Together the vector space of chains $C_k$ form the chain complex $\{C_*,\partial\}$, a graded vector space: $$\ldots\stackrel{\partial}{\rightarrow}C_{n+1}\stackrel{\partial}{\rightarrow}C_{n}\stackrel{\partial}{\rightarrow}\ldots \stackrel{\partial}{\rightarrow}C_{0}\stackrel{\partial}{\rightarrow}0.$$ Meanwhile, together the cochain groups $C^k$ form the cochain complex $\{C^*,d\}$: $$\ldots\stackrel{d}{\leftarrow}C^{n+1}\stackrel{d}{\leftarrow}C^{n}\stackrel{d}{\leftarrow}\ldots \stackrel{d}{\leftarrow}C^{0}\stackrel{d}{\leftarrow}0.$$

Look: the "grading operators" here go in the opposite direction!

So, it's a mistake is to use the term boundary operator, which works on chains, with cochains or differential forms. Cochains (differential forms) need the exterior derivative. The former decreases the dimension/degree while the latter increases.

In general, a cochain complex $C^*$ is any sequence of vector spaces and linear operators (or groups and homomorphisms): $$\ldots\stackrel{\delta}{\leftarrow}C^{n+1}\stackrel{\delta}{\leftarrow}C^{n}\stackrel{\delta}{\leftarrow}\ldots \stackrel{\delta}{\leftarrow}C^{0}\stackrel{\delta}{\leftarrow}0$$ satisfying: $${\rm im \hspace{3pt}} \delta \subset \ker \delta.$$

These vector spaces may be the spaces of differential forms, continuous or discrete, with $\delta=d$ the exterior derivative, or from cochains of cubical complexes or other cell complexes.

The elements of $\ker (\delta)$ are called cocycles and elements of ${\rm im \hspace{3pt}} (\delta)$ are coboundaries.

Whatever the source of the complex, the cohomology now can be computed as the quotient: $${\rm im \hspace{3pt}} \delta / \ker \delta.$$

Note: Differential forms have an extra operation: the wedge product!