This site is being phased out.
Discrete exterior calculus
It's been known for a long time that smooth differential forms form a cochain complex (De Rham, 1931). However the opposite direction of this correspondence has been neglected until recently: co-chains are differential forms. Neglected in what sense?
If a manifold is a cell complex (cubical complex in the simplest case), co-chains are thought of as discrete differential forms while the co-boundary operator is the exterior derivative. Turns out this is a good way to discretize things, such as PDEs. Better yet, the result is a theory that parallels the smooth calculus. It's discrete calculus rather than discretized calculus.
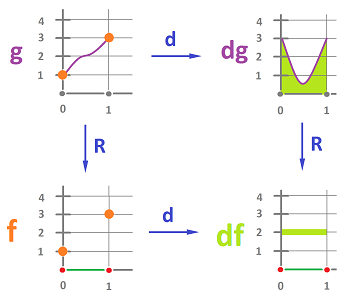
This is an illustration of how calculus can be discretized:
Here, $d$ stands for the exterior derivative and $R$ is the de Rham map. Course:
Project:
It is educational to see the heat PDE next to the heat transfer model written with differential forms: $$ \frac{\partial u}{\partial t}=-\frac{\partial ^2u}{\partial x^2}$$ $$d_t T=-d_x(d_xT)^*,$$ where $d$ is the exterior derivative and * stands for the Hodge duality.
Sources:
- Image model based on n-pixels and defined in algebraic topology
- Discrete Exterior Calculus by Hirani
- Discrete Differential Forms for Computational Modeling by Desbrun, Kanso, Tong
- Discrete Calculus: Applied Analysis on Graphs for Computational Science by Grady and Polimeni
Inexplicably, cubical complexes are mostly ignored in the discrete exterior calculus literature. The reason must be the inertia from the decades of having to deal with meshes. Of course, discretization on a square grid is easy...