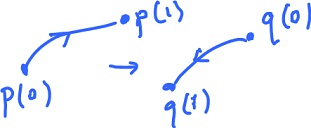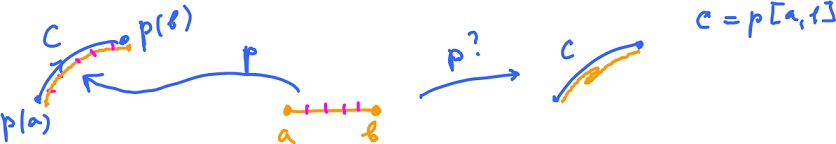This site is being phased out.
Vector integrals
Contents
Introduction
Consider two main types of integrals we have seen.
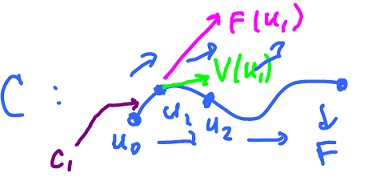
Given motion with the position function $F : {\bf R} {\rightarrow} {\bf R}^n$ during a time interval $[ a, b ]$, we have two main "length characteristics":
- The displacement $= F(b) - F(a) = \displaystyle\int_a^b F'(t) dt = \displaystyle\int_a^b V(x) dx$,
where $V(t)$ is the velocity. (Also the work integral.)
- The distance traveled $= \displaystyle\int_a^b || F'(t) || dt$,
where curve $C$ is the image of $F$, so this is the arc length of a parametric curve. (Also the surface area integral.)
The usual, displacement integral satisfies these properties.
Linearity:
$$\displaystyle\int_G ( f(x) + g(x) ) dx = \displaystyle\int_G f(x) dx + \displaystyle\int_G g(x) dx {\rm \hspace{3pt} (Sum \hspace{3pt} Rule)}$$
$$\displaystyle\int_G k f(x) dx = k \displaystyle\int_G f(x) dx {\rm \hspace{3pt} (Constant \hspace{3pt} Multiple \hspace{3pt} Rule)}$$
Additivity:
$$\displaystyle\int_{A \cup B} f(x) dx = \displaystyle\int_a f(x) dx + \displaystyle\int_B f(x) dx, {\rm \hspace{3pt} with \hspace{3pt}} (A \cap B) = 0, {\rm \hspace{3pt} in \hspace{3pt} particular}$$
$$\displaystyle\int_{[a,b] \cup [c,d]} f(x) dx = \displaystyle\int_{[a,b]} f(x) dx + \displaystyle\int_{[c,d]} f(x) dx$$
But these properties don't fully apply to the arc length integral. What is the difference?
Observe how differently the two integrals behave when the motion changes direction, from $b$ to $a$:
$$\displaystyle\int_a^b V(x) dx = - \displaystyle\int_B^a V(x) dx,$$
$$\displaystyle\int_a^b || F'(t) || dt = \displaystyle\int_B^a || F'(t) || dt.$$
Orientation:
$$\displaystyle\int_{-[a,b]} f(x) dx = - \displaystyle\int_{[a,b]} f(x) dx = \displaystyle\int_{[b,a]} f(x) dx$$
The difference comes from either treating the intervals as
or as
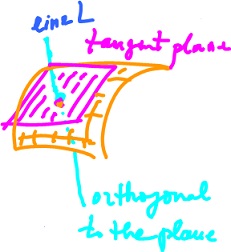
Orientation of curves and surfaces
We want to compute the flow of liquid through a region in space. For that we need to understand the direction of the flow with respect to the orientation of the surface it passes through. There are two ways to do specify the orientation:
- orient the curve that bounds the region and then use the "screw rule" to find the corresponding normal vector to the surface; and
- look at the tangent plane to the surface and deal with its orientation which is simply a choice of the normal vector.
The orientation of a curve comes from its parametrization. For the curves in figure there are two possible orientations (and infinite many parametrizations). For example, given parametrization $p(s)$,
$$q(s) = p(1 - s)$$
is another parametrization that produces the opposite orientation to the one from $p$.
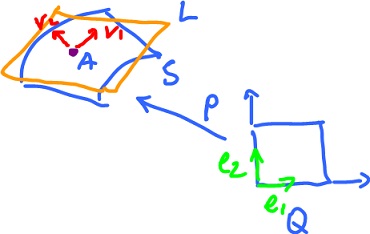
We can approach the orientation of surfaces in a similar manner. Indeed, the orientation of a surface comes from its parametrization (at least locally). Let's understand orientation of the square, $Q$, in space first. We can still look at it as corresponding to the direction of the parametric curve (closed curve) that bounds the square. This is a more direct way.
Parametrize $Q$ as a map from a square in the plane to the $3$ dim space:
$$R_2(s,t) = t,$$
$$R_3(s,t) = 0,$$
with
$$R : {\bf R}^2 {\rightarrow} {\bf R}^3.$$
What is the orientation? It is a unit vector perpendicular to both $R(e_1)$ and $R(e_2)$, where $e_1, e_2$ are the (fixed) basis vectors of ${\bf R}^2$. So, if $L$ is a line perpendicular to the square (or a surface), then the orientation is a basis for $L$ with unit vectors. And there are exactly two choices.
Note: the alternative parametrization of Q gives the opposite orientation:
$$R_1(s,t) = (1 - s),$$
$$R_2(s,t) = t,$$
$$R_3(s,t) = 0.$$
The orientation of a surface is determined by the orientation of its tangent plane (hyperplane) $L$. The set of all vectors perpendicular to $L$ is a vector subspace of dimension $1$. There are two possible unit vectors in it. Choosing one of them corresponds to fixing the orientation.
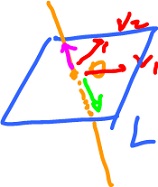
Suppose $n = 3$. Then how do we find these vectors? Given a basis of $L$, say $v_1$ and $v_2$, we take as unit vector $u$, defined as
$$u = \frac{v_1 \times v_2}{|| v_1 × v_2 ||}.$$
Where does the basis of $L$ come from? From the parametrization.
$$p( 0, 0 ) = A$$
$$v_1 = ?$$
$$v_2 = ?$$
The basis $\{ v_1, v_2 \}$ comes from $Q$ by means of $p$:
$$v_1 = p'( 0, 0 ) e_1,$$
$$v_2 = p'( 0, 0 ) e_2.$$
Let's go back to curves. Given a parametrization
$$p: [ a, b ] {\rightarrow} {\bf R}^n, $$
A parametrization that isn't one-to-one (on the right) is not good for computing the arc length, but fine for line integrals: displacement, work, etc. Same applies to surface integrals.
For more see Orientation.
Work
Suppose we want to compute the work $W$ of a constant force $F$ along a straight path. As we know in this case
$$W = force \cdot distance.$$
This simple formula though only works if we take into account the direction of motion. Consider the special case when you move forward and then back. Then the work breaks into two parts and they cancel each other. To clarify the situation, we parametrize the motion as:
$$p: [ 0, 2 ] {\rightarrow} C = [ 0, 1 ], $$
$$\begin{array}{} p(t) &= t & {\rm \hspace{3pt} if \hspace{3pt}} t \in [0,1], p'(t)=1, \\ &=(2-t) & {\rm \hspace{3pt} if \hspace{3pt}} t \in [1,2], p'(t)=-1 ; \\ p(0) &= p(2) = 0 \end{array}$$
Then,
the velocity $= 1$ during [ 0, 1 ]; $= -1$ during $[ 1, 2 ]$.
Then
The idea is that we should amend the formula as:
where unit velocity is the unit vector in the direction of the motion:
Moreover,
with summation over periods of constant velocity and force.
The need for this term becomes clearer in the case ${\rm dim \hspace{3pt}} = 2$.
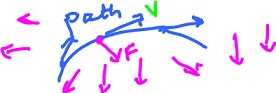
Suppose $V$ is the velocity vector. Observe that
$$W = 0 {\rm \hspace{3pt} if \hspace{3pt}} F \perp V.$$
More generally, $F^*$ matters when calculating the work, $F^*$ being the projection of $F$ on $V$. Thus,
where $s$ is the distance. Note that in this formula $F$ is a vector field.
Example. Find the work
$$W = \displaystyle\sum_i F_i \cdot V_i \cdot {\Delta}s_i$$
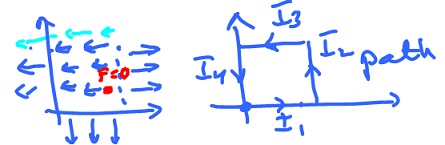
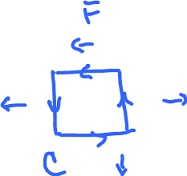
while moving through the force field $F$ displayed along the square path counterclockwise. Observe
$$||F|| = 1, ||V|| = 1.$$
Compute work along each of the straight segments:
$$I_1: W = ( 0, -1 ) ( 1, 0 ) = 0;$$
$$I_2: W = ( 1, 0 ) ( 0, 1 ) = 0;$$
$$I_3: W = ( -1, 0 ) ( -1, 0 ) = 1;0$$
$$I_4: W = ( -1, 0 ) ( 0, -1 ) = 0.$$
Then
$$W = 0 + 0 + 1 + 0 = 1.$$
To summarize, if the force $F$ is constant and the velocity $V$ is constant then the work is found by
$$W = F \cdot V {\Delta}s,$$
where the $\cdot$ is the dot product, $V$ is the unit vector of the velocity and ${\Delta}s$ is the distance.
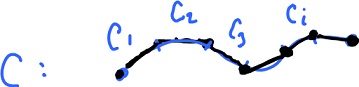
Now what if we have a parametric curve $C$? Then we approximate the curve (and the motion) by a sequence of segments so that with constant $F$ and $V$ in each:
$$F = F_i {\rm \hspace{3pt} on \hspace{3pt}} C_i,$$
$$V = V_i {\rm \hspace{3pt} on \hspace{3pt}} C_i,$$
then
$$W_i = F_i \cdot V_i l(C_i),$$
where $l(C_i)$ is the length of $C_i$.
The total work is then
$$W = \displaystyle\sum_{i=1}^n F_i \cdot V_i l(C_i).$$
We
- approximate the force field with a piecewise constant field;
- approximate the curve with a broken line.
Then
$$W \approx \displaystyle\sum_{i=1}^n F(u_i) \cdot V(u_i) l(C_i),$$
with $C_i$ which goes from $u_{i-1}$ to $u_i$.
Now we define the work as
$$W = \displaystyle\lim_{n \rightarrow \infty} \displaystyle\sum_{i=1}^n F(u_i) \cdot V(u_i) l(C_i).$$
If we assume that such a limit exists (it does when $F$ is continuous and the curve is continuously differentiable), then we define the line integral
$$\displaystyle\int_C F \cdot V ds $$
as this limit (here $F \cdot V ds$ is a differential form).
Exercise. Suppose this is the force field and the path. Applying the above definition to this example, the expression
$$\displaystyle\lim_{n \rightarrow \infty} \displaystyle\sum_{i=1}^n ...$$
will have constant terms, so it stabilizes... finish.
Example. Let
$$F( x, y ) = ( x + y, x^2 y ),$$
$$F \cdot V ds = ( x + y, x^2 y ) \cdot ( dx, dy ) = ( x + y ) dx + x^2 y dy.$$
So the work is equal to
$$W = \displaystyle\int_C ( x + y ) dx + x^2 y dy.$$
Now we need a parametrization, and we choose to parametrize $C$ as:
$$p: [ a, b ] {\rightarrow} {\bf R}^2;$$
$$u_i = p(t_i)$$
$$\begin{array}{} \displaystyle\int_C ... &= \displaystyle\lim_{n \rightarrow \infty} \displaystyle\sum_{i=1}^n F(u_i) \cdot V(u_i) l(C_i) \\ &\approx \displaystyle\lim_{n \rightarrow \infty} \displaystyle\sum_{i=1}^n F(u_i) \cdot \frac{p'(t_i)}{||p'(t_i)||} ||p'(t_i)|| {\Delta}t, \end{array}$$
where we have expressed the velocity unit vector as $\frac{p'(t_i)}{||p'(t_i)||}$, and the the distance covered in the time interval ${\Delta}t$ as the product $||p'(t_i)|| {\Delta}t$ (speed $\cdot$ time). And thus we have
$$\displaystyle\int_C ... = \displaystyle\lim_{n \rightarrow \infty} \displaystyle\sum_{i=1}^n F(u_i) \cdot p'(t_i) {\Delta}t,$$
which is a Riemann sum, with parametrization $p$, whose limit $n {\rightarrow} \infty$ defines the Riemann integral
$$\displaystyle\int_a^b F( p(t) ) \cdot p'(t) dt.$$
Example. Compute the line integral
$$\displaystyle\int_C 2x dx + 6( x - y ) dy {\rm \hspace{3pt} with}$$
$$C: p(t) = ( t, t ), 0 \leq t \leq 1.$$
Here the force is $F = ( 2x, 6( x - y) )$, while $dW = ( dx, dy )$. Moreover, $a = 0$ and $b = 1$.
Since
$$p'(t) = ( 1, 1 ),$$
the Riemann integral turns out to be
$$\begin{array}{} \displaystyle\int_C F \cdot dW &= \displaystyle\int_a^b ( 2t, 6( t - t ) ) \cdot ( 1, 1 ) dt \\ &= \displaystyle\int_0^1 ( 2t, 0 ) \cdot ( 1, 1 ) dt \\ &= \displaystyle\int_0^1 2t dt \\ &= t^2 |_0^1 \\ &= 1. \end{array}$$
Examples of line integrals
Example. Compute
$$\displaystyle\int_C ( x_2, x_3, x_1 ) \cdot dX, {\rm \hspace{3pt} where}$$
$$C: p(t) = ( {\rm cos}(t), {\rm sin}(t), t ) = ( X_1, X_2, X_3 ), 0 \leq t \leq 2{\pi}.$$
In this case we have
$$F( x_1, x_2, x_3 ) = ( x_2, x_3, x_1 )$$
and
$$p'(t) = ( -{\rm sin}(t), {\rm cos}(t), 1 ).$$
Putting everything together one obtains
$$\begin{array}{} \displaystyle\int_C ... &= \displaystyle\int_a^b F( p(t) ) \cdot p'(t) dt \\ &= \displaystyle\int_0^{2 \pi} ( {\rm sin}(t), t, {\rm cos}(t) ) \cdot ( -{\rm sin}(t), {\rm cos}(t), 1 ) dt \\ &= \displaystyle\int_0^{2 \pi} ( -{\rm sin}^2(t) + t{\rm \hspace{3pt} cos}(t) + {\rm \hspace{3pt} cos}(t) ) dt. \end{array}$$
Here then one integrates, the first term through a change of variables $u = {\rm \hspace{3pt} cos}(t)$, the second term by parts, and the last term directly.
Example. Compute $\displaystyle\int ( 2x dx + 6( x - y ) dy )$ with
Now parametrize $C$:
$$p(t) = ( t, -t ), {\rm \hspace{3pt} with \hspace{3pt}} -1 \leq t \leq 2.$$
Then
$$p'(t) = ( 1, -1 ).$$
Finally,
$$\begin{array}{} \displaystyle\int ... &= \displaystyle\int_{-1}^2 ( 2t, 6( t + t ) ) \cdot ( 1, -1 ) dt \\ &= \displaystyle\int_{-1}^2 ( -10t ) dt = -5t^2 |_{-1}^2 \\ &= -20 + 5 \\ &= -15. \end{array}$$
Properties of line integrals
Additivity:
$$\displaystyle\int_{C_1 \cup C_2} F \cdot dX = \displaystyle\int_{C_1} F \cdot dX + \displaystyle\int_{C_2} F \cdot dX.$$
Here the parametrizations should match
$$C_1 {\cup} C_2: [ a, c ] {\longleftrightarrow} C_1: [ a, b ] \& C_2: [ b, c ].$$
Linearity:
$$\displaystyle\int_C ( F + G ) \cdot dX = \displaystyle\int_C F \cdot dX + \displaystyle\int_C G \cdot dX;$$
$$\displaystyle\int_C ( k F ) \cdot dX = k \displaystyle\int_C F \cdot dX.$$
(follow from the formula)
We now know that
$$\displaystyle\int_C F \cdot dX = \displaystyle\int_a^b F( p(t) ) \cdot p'(t) dt;$$
what can we say if $||F|| \leq M$? We consider
$$\begin{array}{} | \displaystyle\int_C F \cdot dX | &= | \displaystyle\int_a^b F( p(t) ) \cdot p'(t) dt | \\ &\leq \displaystyle\int_a^b | F( p(t) ) \cdot p'(t) | dt \\ &\leq \displaystyle\int_a^b || F( p(t) ) || || p'(t) || dt \\ &\leq \displaystyle\int_a^b M || p'(t) || dt \\ &= M \displaystyle\int_a^b || p'(t) || dt , \end{array}$$
and we recognize $(\displaystyle\int_a^b || p'(t) || dt )$ as the arc length of $C$. It follows then:
Theorem. If $||F|| \leq M$ on $C$ , then
$$| \displaystyle\int_C F \cdot dX | \leq M \cdot ({\rm \hspace{3pt} length \hspace{3pt} of \hspace{3pt}} C).$$
If we reverse orientation of the curve, we get
$$C: X = p(t), t {\in} [ a, b ];$$
$$-C: q(t) = p( b + a - t ), t {\in} [ a, b ];$$
$$q'(t) = -p'( b + a - t).$$
It follows then:
Theorem. If $(-C)$ is $C$ with reversed orientation, then
$$\displaystyle\int_{-C} F \cdot dX = - \displaystyle\int_C F \cdot dX.$$
Orthogonality. If $C$ is vertical (horizontal) in ${\bf R}^2$, and $F = ( f_1, 0 ) ( F = ( 0, f_2)$, respectively ), then
$$\displaystyle\int_C F \cdot dX = 0.$$
Proof. Easy:
$$C: p(t) = ( 0, r(t) ), t {\in} [ a, b ];$$
Then,
$$\begin{array}{} \displaystyle\int_C ( f_1, 0 ) \cdot dX &= \displaystyle\int_a^b ( f_1(t), 0 ) \cdot ( 0, r'(t) ) dt \\ &= \displaystyle\int_a^b ( f_1(t) \cdot 0 + 0 \cdot r'(t) ) dt = 0. QED \end{array}$$
It follows then the integral along the circle that lies in the $x_2x_2$-plane for the force along the $x_a$ axis is $0$:
$$\displaystyle\int_a^b ( f_1, 0, 0, ) \cdot ( 0, r'(t), s'(t) ) dt = 0.$$
with
$$r(t) = {\rm \hspace{3pt} cos}(t);$$
$$s(t) = {\rm \hspace{3pt} sin(t)}.$$
The integral after parametrization becomes
$$\displaystyle\int_0^{2 \pi} ( f r'(t) - f s'(t) ) dt = ?$$
(here the integrand is different from zero).
Se also Stokes theorem and Independence of path.