This site is being phased out.
Cell complex
Contents
Gluing cells together
With such a topological tool as quotient available to us, we can construct anything imaginable starting from almost anything. We would like, however, to learn how to build things from the elementary pieces, cells, and do it in a gradual and orderly manner. The point is to be able to build and compute homology, and do it in a gradual and orderly manner.
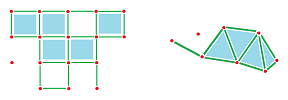
One can see examples of things created from elementary pieces appear in real life, such as these balls sewn from patches of leather:
We already have seen two ways to construct topological spaces from cells. Cubical sets are unions of cubes of various dimensions and the realizations of simplicial complexes are combinations of homeomorphic images of simplices of various dimensions:
In either of these examples, we orderly glue edges to each other at their end-points. But, those end-points are $0$-cells. Furthermore, we glue $2$-cells to each other along their edges. And, those edges are $1$-cells. And so on.
The main difference is in the manner these cells are found. In the case of cubical complexes, cells are subsets of a given Euclidean space, while simplicial complexes are built from data and its cells can then be realized in a Euclidean space.
Exercise. The difference is that the cells of cubical complexes are homeomorphic to cubes and squares, while the cells of simplicial complexes are homeomorphic to simplices and triangles. Explain the difference. Hint: joke.
One real difference is the number of adjacent cells each cell has: $4$ for a square and $3$ for a triangle, which dictates the manner they are attached to each other. We would like to develop a unified approach to such gluing constructions. Cell complexes have cells of arbitrary shape with arbitrary number of neighbors.
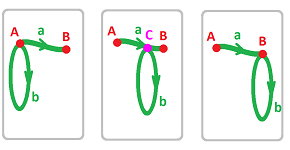
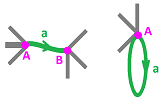
Example (circle). The simplest cubical complex we could use to represent the topological circle consists of four edges arranged in a square. But why should we need four pieces when we know that a circle can be built from a single segment with the end-points glued together? In fact, the number one example of identification is gluing the end-points of a segment to create a circle. The latter will have just one $1$-cell in contrast to the realizations we have seen, i.e., $4$ for a cubical complex and $3$ for a simplicial complex:
The homology and how it is computed is very revealing. For the first two cases, we already know the answers:
- cubical: $H_1=< [a+b+c+d] > \cong {\bf R}$;
- simplicial: $H_1=< [a+b+c] > \cong {\bf R}$.
The third case will be much simpler with so few cells:
- $0$-cells: $A$;
- $1$-cells: $a$.
Certainly, this is not a cubical complex because we can't place these cells on a grid. However, the possibility of homological analysis remains since the boundary operator still makes sense: $$\partial a = A - A = 0.$$ Further, the chain complex is: $$\partial = 0 : C_1 = < a > \to C_0 =< A >.$$ Then the homology $H_1$ is generated by the homology class of $a$: $$H_1 = < [a] > \cong {\bf R}.$$
Thus, the result is the same in all the three cases, as expected:
It is, in a way, the same chain! Of course, the group can also be generated by the counterclockwise chain.
$\square$
Exercise. Provide a similar analysis for the sphere.
Examples and definitions
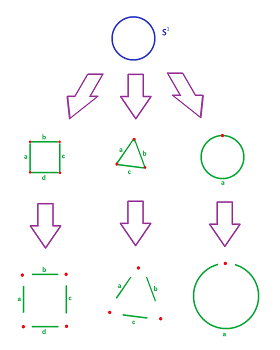
We are already familiar with gradual and orderly building -- via skeleta -- of cubical and simplicial complexes:
The only difference is that now we have more flexibility about the cells. Topologically they are balls of various dimensions:
Definition. A (closed) $n$-cell $a$ is a topological space homeomorphic to the closed $n$-ball $${\bf B}^n:=\{ x\in {\bf R}^n:\ ||x|| \le 1 \}.$$ The image of the frontier of ${\bf B}^n$ in ${\bf R}^n$ under this homeomorphism $h:{\bf B}^n \to a$ is called the boundary of the cell $$\partial a := h(\operatorname{Fr}({\bf B}^n)).$$ Also, the image of the interior, and the complement of the boundary, is denoted by $$\dot{a} = a \setminus \partial a,$$ and may be called the “inside” of the cell.
$\square$
Proposition. The definition of the boundary is topological in the sense that under homeomorphisms of cells, boundary is mapped to boundary.
Exercise. Prove the proposition. Hint: note the difference between the topology of a small neighborhood of a point in the frontier and that of a point in the interior of the ball.
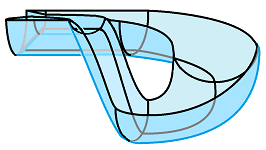
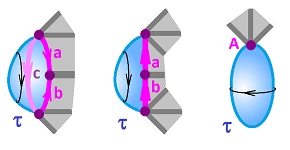
Example (ladle). Let's consider a specific example. Suppose we want to build something that looks like a ladle, which is the same topologically as a Ping-Pong bat:
We want to create a simple topological space from the ground up, using nothing but cells and quotients, in fact,
In our box, we have: the parts, the glue, the schematics, and a set of instructions of how to build it.
This is the schematics:
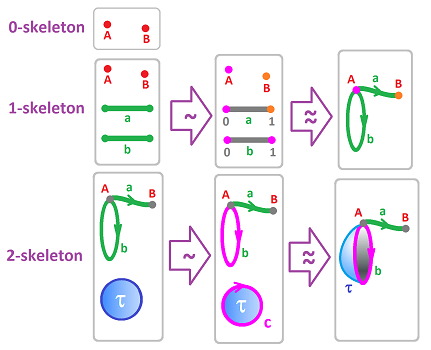
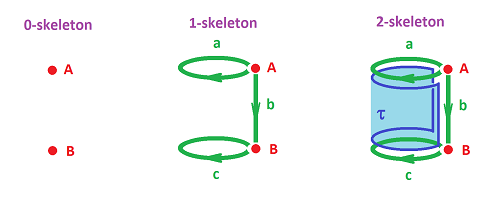
Let's narrate the instructions. We start with the list $K$ of all cells arranged according to their dimensions:
- dimension $0$: $A,B$;
- dimension $1$: $a,b$;
- dimension $2$: $\tau$.
These are the building blocks. At this point, they may be arranged in a number of ways.
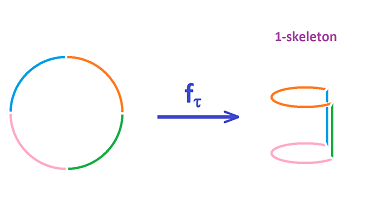
Now, the two points $A,B$ are united into one topological space -- as the disjoint union. That's the $0$-skeleton $K^{(0)}$ of $K$.
Next, we take this space $K^{(0)}$ and combine it, again as the disjoint union, with all $1$-cells in $K$. To put them together, we introduce an equivalence relation on this set. However, to keep this process orderly, we limit ourselves to an equivalence relation between the vertices (i.e., the elements of $K^{(0)}$, and the boundaries of the $1$-cells we are adding. In other words, we identify the end-points of $a$ and $b$ to the points $A$ and $B$. This can happen in several ways. We make our choice by specifying the attaching map for each $1$-cell thought of as a segment $[0,1]$: $$f_a:\partial a\to K^{(0)},\ f_b:b\to K^{(0)} ,$$ by specifying the values on the end-points: $$f_a(0)=A,\ f_a(1)=B,\ f_b(0)=A,\ f_b(1)=A.$$ We use these maps following the attaching rule: $$x\sim y \Leftrightarrow f_a(x)=y.$$ The result is the $1$-skeleton $K^{(1)}$.
The rule we followed was to choose
Next, we take this space $K^{(1)}$ and combine it, again as the disjoint union, with all $2$-cells in $K$. To put them together we introduce an equivalence relation following the rule above. For this dimension, we identify the edge of $\tau$ with $1$-cell $a$, point by point. This can happen in several ways and we make our choice by specifying the attaching map for the $2$-cell: $$f_{\tau}:\tau\to K^{(1)} .$$ We only need to specify the values on the boundary and we assume that $f_{\tau}:\partial\tau\to b$ is a homeomorphism. We again use the attaching rule: $$x\sim y \Leftrightarrow f_{\tau}(x)=y.$$ The result is the $2$-skeleton $K^{(2)}$, which happens to be the realization of the whole $K$.
$\square$
Exercise. Present the cell complex structures for these two arrangements:
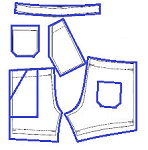
Exercise. (a) Present the cell complex structure for the sewing pattern below (shorts). (b) Do the same for a pair of breakaway pants.
The formal definition of cell complex does not rely on illustrations. It is inductive.
Definition. Suppose we have a finite collection of (unrelated to each other) cells $K$. Suppose $C^n$ denotes all $n$-cells in $K$. Next, the $0$-skeleton $K^{(0)}$ is defined as the disjoint union of all $0$-cells: $$K^{(0)} = \bigsqcup C^0 .$$
Now suppose that the $n$-skeleton $K^{(n)}$ has been constructed. Then the $(n+1)$-skeleton $K^{(n+1)}$ is constructed as follows. Suppose for each $(n+1)$-cell $a$, there is an attaching map $$f_a : \partial a \to K^{(n)}.$$ Then the $(n+1)$-skeleton $K^{(n+1)}$ is defined as the quotient of the disjoint union of the $n$-skeleton $K^{(n)}$ and all the $(n+1)$-cells: $$K^{(n+1)} = (K^{(n)} \bigsqcup C^{n+1})/ _{\sim},$$ where $\sim$ is defined by:
The attaching maps have to satisfy an extra condition:
The resulting topological space is called a realization $|K|$ of cell complex $K$. Often, we will use “cell complex $K$” for both.
$\square$
Without loss of generality, we can assume that the attaching map is extended to $$f_a : a \to K^{(n)},$$ with the only requirement:
- $f_a\Big|_{\dot{a}}$ is a homeomorphism.
In fact, this map may be seen as a restriction of the identification map. Further, since the inclusions of the skeleta into the complex are provided, the attaching map can also be thought of as $$f_a : a \to |K|.$$
Thus, a cell complex $K$ is a combination of the following:
- the collection of cells $K$,
- the skeleta $K^{(0)} \subset K^{(1)} \subset \ ... \ \subset K^{(N)}=|K|$, and
- the attaching maps $f_a:a\to K^{(n)}$, where $a$ is an $n$-cell in $K$.
If this was a building, these would be the inventory, the blueprints, and the daily work orders.
Exercise. Provide an illustration similar to the one above for a topological space that looks like (a) an air-balloon with a thread hanging, (b) a candy apple.
Exercise. Find the cell complex representation of the figure eight.
Exercise. (a) Find the cell complex representation of the surface acquired by cutting the Klein bottle in half. (b) Use the representation to identify the surface.
Example (complex projective plane). First, let $${\bf S}^{2n+1}:=\{z\in {\bf C}^{n+1}:\ ||z||^2=1\}.$$ Recall: $${\bf CP}^n:={\bf S}^{2n+1} / _{\sim},$$ where $$z\sim z' \Leftrightarrow z=e^{i\theta}z'.$$ Then the map $$f_n:{\bf B}^{2n}=\{z\in {\bf C}^{n}:||z|| \le 1\} \to {\bf S}^{2n+1},$$ given by $$f_n(z):= \left (z,\sqrt{1-||z||^2} \right),$$ is the attaching map that makes ${\bf CP}^n$ into a cell complex.
When $n=1$, all points are equivalent. Therefore, ${\bf CP}^1$ is a point. The identification map ${\bf S}^{3} \to {\bf CP}^1 ={\bf S}^{2}$ is called the Hopf map.
$\square$
Exercise. Recall that the (real) projective space is a quotient of the sphere: $${\bf P}^n:={\bf S}^n / _\sim,$$ where $x \sim -x$. Let $q: {\bf S}^n \to {\bf P}^n$ be the identification map of the equivalence relation. What space is produced by attaching ${\bf B}^{n+1}$ to ${\bf P}^n$ by means of $q$?
The topology
Let's observe that $U$ is open in cell complex $K$ if and only if for any $n$-cell $\sigma\in K$, the set $f_{\sigma}^{-1}(U)$ is open. This condition is equivalent to the following: $U\cap \sigma=U\cap f_{\sigma}({\bf B}^n)$ is open. The same is true with “open” replaced with “closed”.
Proposition. Cell complex $K$ has the weak topology, i.e., $U$ is open in $K$ when $U\cap K^{(n)}$ is open for each $n$.
Exercise. Prove the proposition.
Exercise. Prove that a point is closed.
So, a cell complex is a topological space built from simple topological spaces, cells, via the quotient construction. This approach allows us to ignore the question of whether or not it fits into some Euclidean space and rely on the fact that all properties we discuss are purely topological.
Theorem. A cell complex is compact.
Proof. It is easy to see that a finite (disjoint) union of compact spaces is compact. So, the initial union $X$ of the cells of the complex is compact. Now $K = X/ _{\sim}$, thence $K$ is compact as a quotient of a compact space (indeed, it's the image of a compact space under a continuous map). $\blacksquare$
Exercise. Represent the sphere as a cell complex with two $2$-cells, list all cells, and describe/sketch the gluing maps.
Exercise. Below is an object made of two squares connected by four (clockwise) twisted strips. (a) Find its cell complex representation. (b)To what is it homeomorphic? (c) What if some of the strips were twisted the opposite way? (d) Answer these questions for a triangle connected by three twisted strips.
Exercise. Explain how cubical and simplicial complexes can be understood as cell complexes.
Example (cylinder). Let's explore more thoroughly the cell complex structure of the cylinder by explicitly presenting both the skeleta and the gluing maps.
The formulas for the gluing maps for the 1-skeleton are simple. Suppose,
- $a = b = c := [0,1]$,
then
- $f_a(0) := A,\ f_a(1) := A;$
- $f_b(0) := A,\ f_b(1) := B;$
- $f_c(0) := B,\ f_c(1) := B.$
For the $2$-skeleton, we'll use a diagram to present the only gluing map $f_{\tau}$. Since ${\tau}$ is a disk, we only need to show where in $K^{(1)}$ the points on its boundary ${\bf S}^1$ are taken. Below we show the preimages of the $1$-cells in $K^{(1)}$:
- the preimages of the $0$-cells $A, B$ are two points, and
- the preimages of the three $1$-cells $a, b, c$ are one arc, two arcs, one arc, respectively.
$\square$
Exercise. Find other ways to attach a $2$-cell to this $1$-skeleton.
Exercise. Build a box by identifying some of the edges of this template:
Transition to algebra
The way we attach the cells to each other is purposeful. Remember we want to be able to compute the boundary operator in just as orderly a fashion as we build the cell complex. This is the reason why we never attach $k$-cells to other $k$-cells but -- along their boundaries -- to the preexisting $(k-1)$-cells:
Note that, without this extra restriction, the result may look very different from what we expect:
The middle option is unacceptable.
Let's illustrate the acceptable attaching maps.
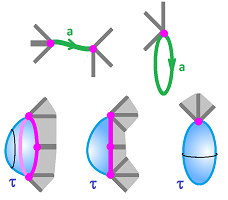
A $1$-cell may be attached to $0$-cells as a rope or as a noose:
Meanwhile, a $2$-cell may be attached to $1$-cells as a soap film, a zip-lock bag, or an air-balloon.
For either dimension, the first of these attaching maps is a homeomorphism and the last is constant. Generally, a cell can be attached along its boundary in a number of ways that include collapses to lower dimensional cells.
The point of the extra restriction on attaching maps is to allow us to proceed directly to algebra as shown below. If the (topological) boundary of an $(n+1)$-cell $\tau$ is the union of several $n$-cells $a, b, c,...$: $$\partial \tau = a \cup b \cup c \cup ...,$$ then the boundary operator evaluated at $\tau$ is some linear combination of these cells: $$\partial _{n+1}(\tau) = \pm a\pm b\pm c\pm...$$
What are the signs? They are determined by the orientation of the cell $\tau$ as it is placed in the cell complex vis-à-vis that of the cells to which it is attached. Let's consider this matching in lower dimensions.
In dimension $1$, the meaning of orientation is simple. It is the direction of the $1$-cell as we think of it as a parametric curve. Then the boundary is the last vertex it is attached to minus the first vertex.
Here, if the (topological) boundary of the $1$-cell $a$ is identified, by the attaching maps, with the union of two $0$-cells $A, B$ (or just $A$), while the (algebraic) boundary of $a$ is the sum (or a linear combination) of $A, B$: $$\begin{array}{lllllll} f_a(\partial a) &= \{A,B\} &\leadsto &\partial _1 (a) = B-A;\\ f_a(\partial a) &= \{A\} &\leadsto &\partial _1 (a) = A-A=0. \end{array}$$
For a $2$-cell, a direction is chosen for its circular boundary, clockwise or counterclockwise. As we move along the boundary following this arrow, we match the direction to that of each $1$-cell we encounter:
Here, we have three cases: $$\begin{array}{lllllll} f_{\tau}(\partial \tau) &= a \cup b \cup c &\leadsto& \partial _2\tau &= a - b - c;\\ f_{\tau}(\partial \tau) &= a \cup b &\leadsto& \partial _2\tau &= -a - b +a+b=0;\\ f_{\tau}(\partial \tau) &= A &\leadsto & \partial _2\tau &= 0. \end{array}$$
Initially, we can understand the orientation of a cell as an ordering of its vertices, just as we did for simplicial complexes.
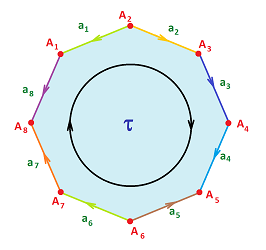
Example. Let's evaluate the boundary operator for this $2$-cell, with the orientations of $1$-cells randomly assigned.
We have: $$\partial \tau = -a_1 + a_2 + a_3 + a_4 - a_5 + a_6 + a_7 - a_8.$$ Further, $$\begin{array}{llll} \partial (\partial \tau) &=& \partial( -a_1 + a_2 + a_3 + a_4 - a_5 + a_6 + a_7 - a_8 ) \\ &=& -\partial a_1 + \partial a_2 + \partial a_3 + \partial a_4 - \partial a_5 + \partial a_6 + \partial a_7 - \partial a_8 \\ &=& -(A_1 - A_2) + (A_3 - A_2) + (A_4 - A_3) + (A_5 - A_4) \\ && - (A_5 - A_6) + (A_7 - A_6) + (A_8 - A_7) - (A_8 - A_1) \\ &=& 0. \end{array}$$
$\square$
The meaning of orientation in higher dimensions will be discussed later.
Theorem. The $k$-homology of a cell complex is fully determined by its $(k+1)$-skeleton.
Exercise. Prove the theorem.
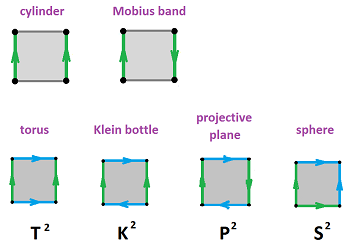
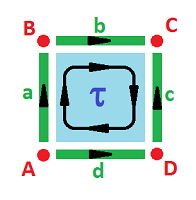
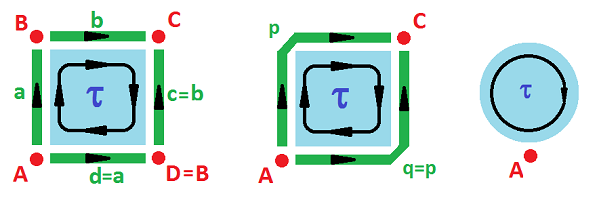
What we can make from a square
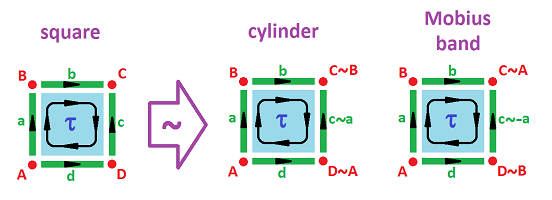
Let's see what we can build from the square by gluing one or two pairs of its opposite edges. We will compute the homology of these surfaces:
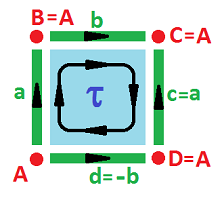
Example (square). This is the simplest cell complex representation of the square even though the orientations can be arbitrarily flipped:
The complex $K$ of the square is:
- $0$-cells: $A, B, C, D$;
- $1$-cells: $a, b, c, d$;
- $2$-cells: $\tau$;
- boundary operator: $\partial \tau = a + b + c - d; \ \partial a = B-A, \partial b = C-B$, etc.
$\square$
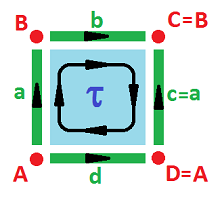
Example (cylinder). We can create the cylinder $C$ by gluing two opposite edges with the following equivalence relation: $(0,y) \sim (1,y)$. The result of this equivalence relation of points can be seen as equivalence of cells: $$a \sim c;\ A \sim D,\ B \sim C.$$
We still have our collection of cells (with some of them identified) and only the boundary operator is different:
- $\partial \tau = a + b + (-a) - d = b - d ;$
- $\partial a = B-A,\ \partial b = B-B=0,\ \partial d = A-A = 0.$
The chain complex is: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lcccccccccc} & & C_{2} & \ra{\partial} & C_{1} & \ra{\partial} & C_0 \\ & & < \tau > & \ra{?} & < a,b,d > & \ra{?} & < A,B > \\ & & \tau & \mapsto & b - d \\ & & & & a & \mapsto & B-A \\ & & & & b & \mapsto & 0 \\ & & & & d & \mapsto & 0 \\ {\rm kernels:} & & Z_2 = 0 && Z_{1} = < b,d > & & Z_{0} = < A,B > \\ {\rm images:} & & B_2 = 0 && B_{1} = < b - d > & & B_{0} = < B-A > \\ {\rm quotients:}& & H_2 = 0 && H_{1} = < [b]=[d] >\cong {\bf Z}& & H_{0} = < [A]=[B] > \cong {\bf Z} \end{array}$$ Here, “kernels” are the kernels of the maps to their right, “images” are the images of the maps to their left.
So, the homology is identical to that of the circle!
$\square$
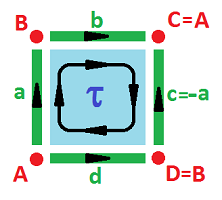
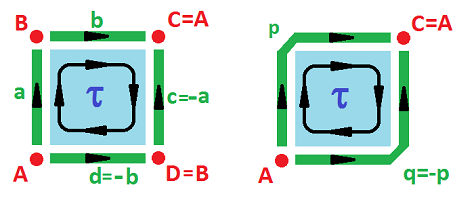
Example (Möbius band). In order to build the Möbius band ${\bf M}^2$, we use the equivalence relation: $(0,y) \sim (1,1-y)$. Once again, we can interpret the gluing as equivalence of cells, $a$ and $c$. But this time they are attached to each other with $c$ upside down. It makes sense then to interpret this as equivalence of cells but with a flip of the sign: $$c \sim -a.$$ Here $-c$ represents edge $c$ with the opposite orientation:
In other words, this is equivalence of chains. Further, $$A \sim D, \ B \sim C.$$ The boundary operator is:
- $\partial \tau = a + b - (-a) - d = 2a + b - d;$
- $\partial a = B-A, \ \partial b = A-B, \ \partial d = B-A.$
The chain complex is: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lcccccccccc} & & C_{2} & \ra{\partial} & C_{1} & \ra{\partial} & C_0 \\ & & < \tau > & \ra{?} & < a,b,d > & \ra{?} & < A,B > \\ & & \tau & \mapsto & 2a + b - d \\ & & & & a & \mapsto & B-A \\ & & & & b & \mapsto & A-B \\ & & & & d & \mapsto & B-A \\ {\rm kernels:} & & Z_2 = 0 && Z_1 = < a+b,a-d > & & Z_0 = < A,B > \\ {\rm images:} & & B_2 = 0 && B_1 = < 2a+b-d > & & B_0 = < B-A > \\ {\rm quotients:}& & H_2 = 0 && H_1 = < [b-d] >\cong {\bf Z} & & H_0 = < [A]=[B] > \cong {\bf Z} \end{array}$$ The bad news is that the homology is the same as that of the cylinder, which means that it doesn't detect the twist of the band. The good news is that the algebra reveals something that we may have missed: the hole in the Möbius band is captured by chain $b-d$, which is the whole edge of the band:
$\square$
Example (sphere). We can either build it as a quotient of the square or, easier, we just combine these pairs of the consecutive edges:
Then we have only two edges left. Even better, we avoid $1$-cells altogether in the last example.
$\square$
Exercise. Compute the homology for all three.
Example (projective plane). It comes from a certain quotient of the disk, ${\bf B}^2/_{\sim}$, where $u \sim -u$ is limited to the boundary of the disk. It can also be seen as a quotient of the square:
As we see, the edge of the disk is glued to itself, with a twist. Its algebraic representation is almost the same as before: $p\sim -p$. In fact, the presence of a degree $2$ homology class, $2p \sim 0$, causes the homology group to have torsion!
Let's compute the homology:
- $2$-cells: $\tau$ with $\partial\tau = 2p$;
- $1$-cells: $p$ with $\partial p = 0$;
- $0$-cells: $A$ with $\partial A = 0$.
Then the $1$-homology is $$\begin{array}{llllll} H_1({\bf P}^2; {\bf Z}) &= < p > / < 2p > &= {\bf Z} / 2{\bf Z} &\cong {\bf Z}_2 ,\\ H_1({\bf P}^2;{\bf Z}_2) &= < p > / < 2p > &= < p > / 0 &\cong {\bf Z}_2 ,\\ H_1({\bf P}^2;{\bf R}) &= \operatorname{span}(p) / \operatorname{span}(2p) &= \text{span}(p) / \operatorname{span}(p) &\cong 0. \end{array}$$ So, the integer and binary homology detect the twist but the real homology doesn't. What happens is that, because of the twist of the $2$-cell, the image of $\partial _2$ is generated by $2p$ in all three cases. However, the algebra is different. Over ${\bf R}$, the set of all real multiples of $2p$ coincides with that of $p$: $\operatorname{span}(2p) = \operatorname{span}(p)$. As a result, the information about the twist is lost. The real numbers are for measuring, not counting!
Another way to see what causes the difference is below: $$\begin{array}{llllllll} {\bf Z}: \quad &\partial \tau = 2p \Longrightarrow &&\text{ nothing}.\\ {\bf Z}_2: \quad &\partial \tau = 2p \Longrightarrow &\partial \tau = 0 \Longrightarrow &\tau \text{ is a cycle, so?}\\ {\bf R}:\quad &\partial \tau = 2p \Longrightarrow &\partial \left(\frac {1}{2}\tau \right)=p \Longrightarrow &p \text{ is a boundary}. \end{array}$$
And here's the rest of the integral homology: $$H_2({\bf P}^2) = 0, \ H_0({\bf P}^2) = {\bf Z}.$$ $\square$
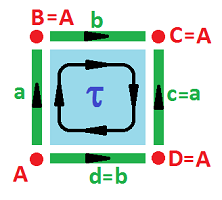
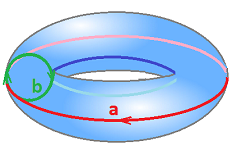
Example (torus). What if after creating the cylinder by identifying $a$ and $c$ we then identify $b$ and $d$? Like this: $$c \sim a,\ d \sim -b.$$ The result is the torus ${\bf T}^2$:
Note how all the corners of the square come together in one. Then the chain complex has very few cells to deal with: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lcccccccccc} & & C_{2} & \ra{\partial} & C_{1} & \ra{\partial} & C_0 \\ & & < \tau > & \ra{?} & < a,b > & \ra{?} & < A > \\ & & \tau & \mapsto & 0 \\ & & & & a & \mapsto & 0 \\ & & & & b & \mapsto & 0 \\ {\rm kernels:} & & Z_2 = < \tau > && Z_1 = < a,b > & & Z_0 = < A > \\ {\rm images:} & & B_2 = 0 && B_1 = 0 & & B_0 = 0 \\ {\rm quotients:}& & H_2 = < \tau > && H_1 = < a,b > & & H_0 = < [A] > \end{array}$$ Thus, the two tunnels in the torus are captured by a longitude and a latitude:
$\square$
Example (Klein bottle). What if we flip one of the edges before gluing? Like this: $$c \sim a,\ d \sim -b.$$
The corners once again come together in one and the chain complex has very few cells to deal with: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lcccccccccc} & & C_{2} & \ra{\partial} & C_{1} & \ra{\partial} & C_0 \\ & & < \tau > & \ra{?} & < a,b > & \ra{?} & < A > \\ & & \tau & \mapsto & 2a \\ & & & & a & \mapsto & 0 \\ & & & & b & \mapsto & 0 \\ {\rm kernels:} & & Z_2 = 0 && Z_1 = < a,b > & & Z_0 = < A > \\ {\rm images:} & & B_2 = 0 && B_1 = < 2a > & & B_0 = 0 \\ {\rm quotients:}& & H_2 = 0 && H_1 = \{ a,b | 2a=0 \} & & H_0 = < [A] > \end{array}$$ Thus, unlike the two tunnels in the torus, this time we have only one captured and the other feature is the "twist".
$\square$
Exercise. What if we flip both? Like this: $$a \sim -c,\ b \sim -d.$$
Exercise. Rewrite the computations of the homology of all six surfaces, over $R={\bf Z}_p$.
Exercise. Compute the integral homology, providing all the details, of the sphere with a membrane inside. Indicate the generators.
Let's summarize the results of these computations: $$\begin{array}{c|c|c|c|c|} R={\bf Z} & {\bf S}^2 & {\bf P}^2 & {\bf T}^2 & {\bf K}^2 \\ \hline H_0 & {\bf Z} & {\bf Z} & {\bf Z} & {\bf Z} \\ H_1 & 0 & {\bf Z}_2 & {\bf Z}\times{\bf Z} & {\bf Z}_2\times{\bf Z} \\ H_2 & {\bf Z} & 0 & {\bf Z} & 0 \end{array}$$ Examining this table tells us a lot about the topological features we thought about at the very beginning of this study.
- The path-components are clearly visible for all spaces.
- The tunnels are present too, along with:
- the twists are new ($1$-dimensional) topological features.
- The voids are here, but
- there are no voids in the projective plane and the Klein bottle. The reason is that the twist makes the two sides of the surface - inside and outside - indistinguishable and then there is no inside or outside.
Exercise. Recreate this table for $R={\bf R}$ and $R={\bf Z}_2$.
Exercise. Sketch the dunce hat and compute its homology:
Exercise. Find a cell complex with the following homology groups: $$H_0={\bf Z},\ H_1={\bf Z}_2,\ H_2={\bf Z}\oplus {\bf Z}.$$
Exercise. In each of the above examples, determine whether this surface separates the space, i.e., whether it is one-sided or two-sided. Hint: it's not same as orientability.
This is how we can create $3$-dimensional complexes. We start with a cube. First, we glue its top and bottom, with each point identified to the one directly underneath. Then we cut the cube into two by a horizontal square.
Then we consider the relations listed above to identify the edges of this square, just as we did for the torus, etc. These relations tell us how the opposite faces of the cube are glued together.
Exercise. Compute the homology produced by this construction, when the square is glued to itself according to each of the above examples.
Homology in dimension n
Cell complexes use very few cells in comparison to cubical and simplicial complexes but the trade-off is the complexity of some of the concepts we have to deal with. In order to develop a complete homology theory for cell complexes, we have to add one missing part: we would need to figure out the meaning of orientation of cells, beyond dimension $2$. With that, we would be able to define the boundary operator $\partial :C_n\to C_{n-1}$ and to prove the property that makes all of this work: $\partial\partial =0$. We will omit these steps and rely, informally, on what we have already developed.
The issue of orientation has been previously developed in full for the following cases:
- $K$ is a cubical complex, and
- $K$ is a simplicial complex.
In addition, the issue is simply moot when
- $K$ is a cell complex but the ring of coefficients is $R={\bf Z}_2$.
For the general cell complexes and arbitrary coefficients, there are two simple enough cases that we can handle. They appear in the highest dimension. For an $n$-cell $\sigma$, we have:
- $\partial _n(\sigma)=0$ when there are no $(n-1)$-cells in $\partial \sigma$;
- $\partial _n(\sigma)=\pm s$ when $s$ is the $(n-1)$-cell in $K$ that forms the boundary $\partial \sigma$ of $\sigma$, and the sign is “+” when there are no other $n$-cells adjacent to $s$.
We use these two cases to compute the homology of the $n$-ball ${\bf B}^n$ and the $(n-1)$-sphere ${\bf S}^{n-1},\ n>2$.
Example (balls). We represent ${\bf B}^n$ as a cell complex as follows.
Cells:
- $n$-cells: ${\sigma}$,
- $(n-1)$-cells: $a$,
- $0$-cells: $A$.
The boundary operator:
- ${\partial}{\sigma} = a,$
- ${\partial}a = 0,$
- ${\partial}A = 0.$
The chain complex and the computation of homology are below: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lcccccccccccccccccccccccccccc} & & C_n(K) & \ra{\partial} & C_{n-1}(K) & \ra{\partial} & C_{n-2}(K) & \ra{\partial} & ... & \ra{\partial} & C_0(K) \\ & & < \sigma > & \ra{\cong} & < a > & \ra{0} & 0 & \ra{0} & ... & \ra{0} & < A > \\ & & {\sigma} & \mapsto & a & \mapsto & 0 & & & & A & \\ {\rm kernels:} & & Z_n = 0 & & Z_{n-1} = < a > & & Z_{n-2} = 0 & & ... & & Z_0 = < A > \\ {\rm images:} & & B_n = 0 & & B_{n-1} = < a > & & B_{n-2} = 0 & &... & & B_0 = 0 \\ {\rm quotients:} & & H_n = 0 & & H_{n-1} = 0 & & H_{n-2} = 0 & & ... & & H_0 = < A > \end{array}$$ $\square$
Example (spheres). The sphere ${\bf S}^{n-1}$ has the same cell complex representation as the ball except the $n$-cell is missing.
The cells:
- $(n-1)$-cells: $a$,
- $0$-cells: $A$.
The boundary operator:
- ${\partial}a = 0,$
- ${\partial}A = 0.$
The chain complex and homology are: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lccccccccccccccccccc} & & C_n(K) & \ra{\partial} & C_{n-1}(K) & \ra{\partial} & C_{n-2}(K) & \ra{\partial} & ... & \ra{\partial} & C_0(K) \\ & & 0 & \ra{0} & < a > & \ra{0} & 0 & \ra{0} & ... & \ra{0} & < A > & \\ & & & & a & \mapsto & 0 & & & & A & \\ {\rm kernels:} & & Z_n = 0 & & Z_{n-1} = < a > & & Z_{n-2} = 0 & & ... & & Z_0 = < A > \\ {\rm images:} & & B_n = 0 & & B_{n-1} = 0 & & B_{n-2} = 0 & & ... & & B_0 = 0 \\ {\rm quotients:} & & H_n = 0 & & H_{n-1} = < a > & & H_{n-2} = 0 & & ... & & H_0 = < A > \end{array}$$ $\square$
In higher dimensions, the algebra tells us about things that we can't see. For example, when the boundary of an $n$-cell is glued to a single point, a new topological feature is created, an $n$-dimensional void.
To summarize our results, we state the following.
Theorem.
- $H_k({\bf B}^n) = 0$ for $k \neq 0$, and $H_k({\bf B}^n) = {\bf R}, \ n = 0, 1, 2, ...$;
- $H_k({\bf S}^n) = 0$ for $k \neq 0,n, $ and $H_0({\bf S}^n) = H_n({\bf S}^n) = {\bf R}, \ n = 2, 3, ...$
Exercise. Solve the problem for $n = 1, 2$.
Quotients of chain complexes
Next, we explore how to compute the chain complex, and then the homology groups of a cell complex in the way it is built -- gradually.
Example (circle). Recall how we computed the homology of the circle. Its chain complex is: $$\partial = 0 \colon C_1 = < a > \to C_0 =< A >.$$ Then it follows $$H_1 = < a > \cong {\bf Z}, \ H_0 = < A > \cong {\bf Z}.$$ It is built from the segment via the quotient construction, point-wise or cell-wise. But we have also seen examples when these identifications are interpreted algebraically, chain-wise.
Let's follow this alternative route. We assume that we initially have the (cubical) complex $K$ of the segment:
- $0$-cells: $A, B$,
- $1$-cells: $a$,
- boundary operator: $\partial a = B-A$.
Its chain complex is $$\partial : C_1(K)=< a > \to C_0(K)=< A,B >.$$ Now to build the circle, we identify $A$ and $B$, $A \sim B$, but this time not as points but as $0$-chains. The outcome of this construction is not the quotient of topological space $|K|$ or even of cell complex $K$ but the quotient of the chain group $C_0(K)$! The result is easy to present and compute algebraically: $$C_0 (K) / _{\sim} = < A,B > / < A-B > = < A,B|A=B > \cong < A >.$$ The new boundary operator is the quotient of the old and it is trivial: $$\partial' =q\partial =0: C_1(K)=< a > \to C_0(K)/ _{\sim} = < A >.$$ Here $q$ is the identification function of this equivalence relation. It immediately follows that $$H_0=< A >.$$ The result is the same as that of the original analysis.
$\square$
Things are more complicated in higher dimensions when we may have to deal with equivalence relations for chains of all dimensions.
Example (cylinder). Let's make the cylinder from the square, algebraically.
The complex $K$ of the square is:
- $0$-cells: $A, B, C, D$;
- $1$-cells: $a, b, c, d$;
- $2$-cells: ${\tau}$;
- boundary operator: $\partial (\tau) = a + b - c - d;\ \partial (a) = B-A,\ \partial (b) = C-B,\ \partial (c) = C-D$, etc.
We create a chain complex for the cylinder by identifying a pair of opposite $1$-cells: $$a \sim c.$$ This creates the quotients of the chain groups of $K$ since $a$ and $c$ are their generators.
Further, now the quotients of the boundary operators between these quotients are to be considered: $$[\partial _n]: C_n(K) / _{\sim} \to C_{n-1}(K) / _{\sim}.$$ As was discussed previously, the quotient of an operator is well defined only if the operator maps equivalence classes to equivalence classes, i.e., this diagram commutes: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \begin{array}{cccccccccc} C_n(K) & \ra{\partial _n} & C_{n-1}(K) \\ \da{q} & & \da{q} \\ C_n(K) / _{\sim} & \ra{[\partial _n]} & C_{n-1}(K) / _{\sim}. \end{array}$$ Here, $q$ is the identification function. So, for $n=1$, the equivalence of edges forces of equivalence of vertices: $$A \sim D, B \sim C.$$ The relations are illustrated below:
We compute the quotients of the chain groups: $$\begin{array}{ll} C_2(K) / _{\sim} = < \tau >;\\ C_{1}(K) / _{\sim} = < a,b,c,d > / < a-c > = < [a],[b],[d] >;\\ C_0(K) / _{\sim} = < A,B,C,D > / < A-D,B-C > = < [A],[B] >. \end{array}$$
Then we compute the values of the quotients of the boundary operators: $$\begin{array}{lllllll} &[\partial_2](\tau) &= [\partial_2(\tau)]&= [a + b - c - d] &= [b - d];\\ &[\partial_1]([a]) &= [\partial_1(a)]& = [B-A];\\ &[\partial_1]([b]) &= [\partial_1(b)]& = [C-B] &= 0;\\ &[\partial_1]([d]) &= [\partial_1(d)] &= [D-A] &= 0. \end{array}$$
Now, these operators and groups form a chain complex and we compute the homology: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lcccccccccc} & & < \tau > & \ra{[\partial _2]} & < [a],[b],[d] > & \ra{[\partial _1]} & < [A],[B] >\\ {\rm kernels:} & & Z_2 = 0 && Z_{1} = < [b],[d] > & & Z_{0} = < [A],[B] > \\ {\rm images:} & & B_2 = 0 && B_{1} = < [b - d] > & & B_{0} = < [B-A] > \\ {\rm quotients:}& & H_2 = 0 && H_{1} = < [b]=[d] >\cong {\bf Z}& & H_{0} = < [A]=[B] > \cong {\bf Z} \end{array}$$ The results are the same.
$\square$
Exercise. Verify the claims made in the above example:
- the quotient operators are well defined;
- the square diagram above is commutative for all $n$;
- the sequence of quotient groups is a chain complex.
Exercise. Provide such a homology computation for the Möbius band.
The approach is applicable to any cell complex $K$. As we build the complex $K$ skeleton-by-skeleton: $$K^{(0)} \leadsto K^{(1)} \leadsto ...\leadsto K^{(N)} = K,$$ we also build the chain complex for $K$ step-by-step as follows. $$C(K^{(0)}) \leadsto C(K^{(1)}) \leadsto ...\leadsto C(K^{(N)}) = C(K).$$ Recall that the attaching maps create these equivalence relations. The $n$-cell $\sigma$ to be added to $K^{(n)}$ is treated as a generator to be added to $C(K^{(n)})$ as its boundary $(n-1)$-cells are already present. Then the current chain groups (and the boundary operators) of $K$ are modified via quotient modulo subgroups generated by these boundary cells of $\sigma$.
Exercise. Compute the homology of the double banana:
Exercise. Compute the homology of the “book” with $n$ pages: