This site is being phased out.
Edge detection
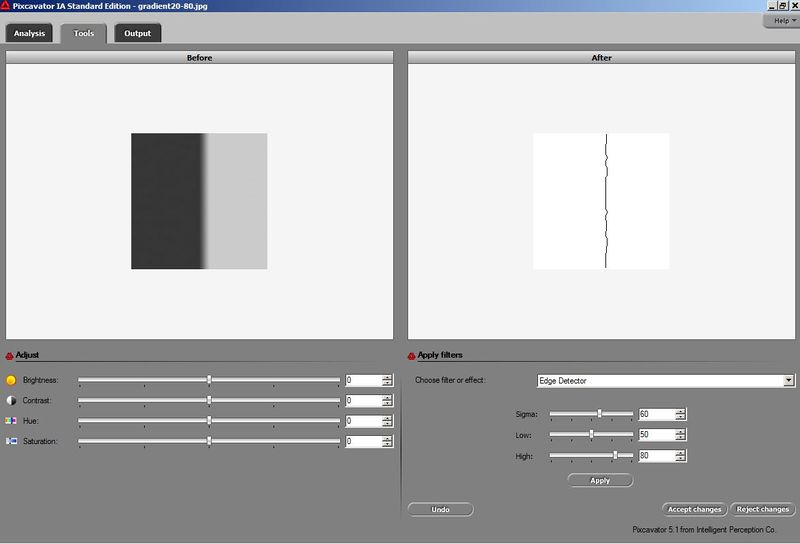
One of the most basic methods of analyzing gray scale image ("image segmentation") is to find the areas of high contrast. These areas are likely to be where an object ends and the the background begins.
More precisely, these are the areas where the change of the gray - for light to dark or dark to light - is the fastest. Then one needs a threshold so that all pixels where this change is higher that this number are considered "edges". To see how it works, try Pixcavator's image processing tools:
Mathematically, we deal with
the rate of change of the gray level = the gradient of the gray scale function.
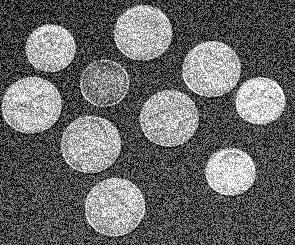
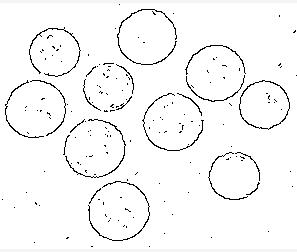
(In fact, one only needs the norm of the gradient.) Computation of the derivative however in the digital (discrete) context is a challenge as it is severely affected by noise. Consider the image of coins and its version with noise added.
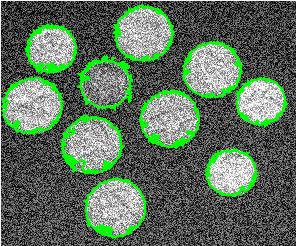
If now edge detection is run, the results are unsatisfactory - too many irrelevant contours. The image with green contours comes from Pixcavator.
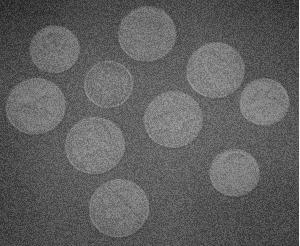
Of course it may be possible to filter out the smaller contours. In this particular case it's impossible because they are parts of large ones. In fact they form large fractal-like structures. This is the reason why edge detection may have to be preceded by smoothing of the image.
Pixcavator's results are also improved by smoothing:
However, the result of smoothing is that the image is changed! At the very least, this affects the accuracy of the measurements.
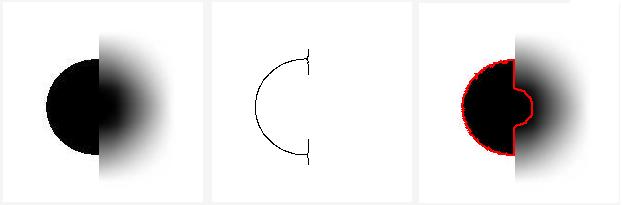
In addition, the resulting contours may be incomplete as in the image above. They aren't closed and, as a result, can't be boundaries of objects. The problem is easier to see with a simpler image, below. It is followed by edge detection and Pixcavator's analysis results:
To read about how Pixcavator resolves the issue of incomplete borders, see Objects in gray scale images.
Still, Pixcavator uses this idea as well, see Border contrast. Keep in mind that even when the contours are closed curves, they may be "nested".