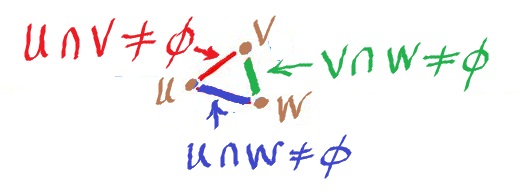This site is being phased out.
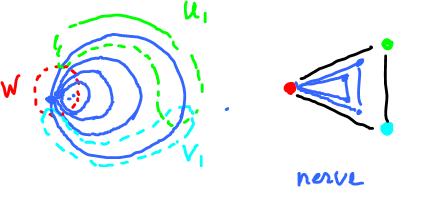
Nerve of cover
Redirect to:
Cell complexes are compact representations of topological spaces, convenient for computing homology and other algebraic invariants. But how do you find this representation if all you have is a topological space, i.e., a collection of open sets.
To solve this problem, let's start with a study of the topology of a simplicial complex.
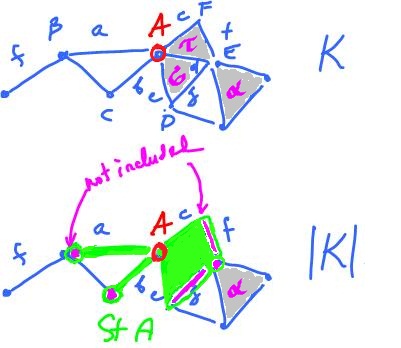
The topology of the realization $|K|$ of such a complex $K$ comes from the topology of each simplex modulo the gluing procedure. Indeed, what makes each complex special is how the simplices are attached to each other because the gluing does not affect the topology of the simplex itself, certainly not its interior. So, we aren't interested in "small" open sets, i.e., ones inside simplices but in "large" open sets that are unions of the interiors of simplices.
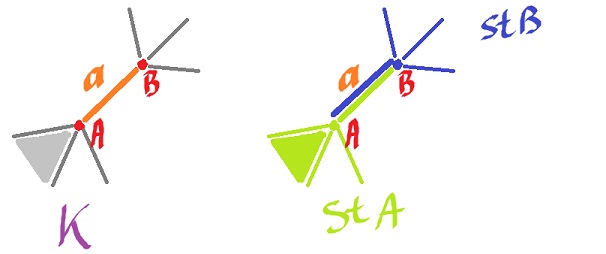
Given a simplicial complex $K$ and a vertex $A$ in $K$, the star of $A$ in $K$ is the collection of all simplices in $K$ that contain $A$: $$St(A) = {σ∈K: A∈σ}.$$ It is easy to prove that this is a subcomplex of $K$. We will also use the word "star" for the union of ${A}$ and the interiors of all the simplices that contain $A$: $$N(A) = \bigcup\{Int(σ): σ∈K, A∈σ\}.$$
Proposition. $N(A)$ is an open subset of $|K|$.
In other words, $N(A)$ is a neighborhood of $A$ which justifies the notation.
Proposition. $\{N(A): A∈K_0\}$ is an open cover of $|K|$.
Exercise. What is $N(B)$ in the image below?
Now we want to construct a simplicial complex from this open cover of $|K|$ and in such a way that it's the same as the original complex $K$? Keep in mind that in its realization the structure of the simplicial complex is lost, like in the image below which is homeomorphic to the one above.
The example below suggests a way to answer this question.
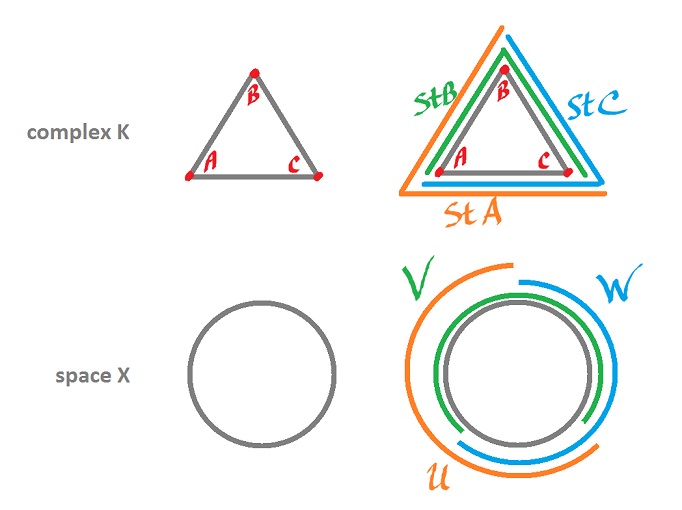
Example. Let's consider the circle as a simple enough example. We start with the simplest triangulation of the circle - a simplicial complex $K$ with three edges with three vertices. Then the stars of vertices consist of two edges each. It's an open cover. Now, suppose $X$ is the circle. The homeomorphism of $|K|$ and $X$ creates an open cover of $X$: three overlapping arcs.
Let $γ = \{U,V,W\}$ be open cover of $X$ that consists of the open sets that came from the stars of the three vertices of $K, St(A), St(B), St(C)$ respectively. What is so special about this cover?
The open sets have non-empty pairwise intersections but the intersection of all three is empty. So what? Observe:
- $U ∩ V ≠ ∅ \Rightarrow N(A) ∩ N(B) ≠ ∅ \Rightarrow A, B$ are connected by an edge,
- $V ∩ W ≠ ∅ \Rightarrow N(B) ∩ N(C) ≠ ∅ \Rightarrow B, C$ are connected by an edge,
- $W ∩ U ≠ ∅ \Rightarrow N(C) ∩ N(A) ≠ ∅ \Rightarrow C, A$ are connected by an edge.
Also observe
- $U ∩ V ∩ W ≠ ∅ \Rightarrow N(A) ∩ N(B) ∩ N(C) ≠ ∅ \Rightarrow A, B, C$ are not connected by a face.
Following this insight we now create a new simplicial complex based entirely on how the elements of this cover intersect.
Let $U,V,W$ be the vertices of complex $L$,
- $U ∩ V ≠ ∅ \Rightarrow U, V$ are connected by an edge,
- $V ∩ W ≠ ∅ \Rightarrow V, W$ are connected by an edge,
- $W ∩ U ≠ ∅ \Rightarrow W, U$ are connected by an edge.
The end result is that there is a 1-1 onto chain map between them! We say that $L$ is isomorphic to $K$.
We can now follow this logic to create simplicial complexes from any open cover of any topological space:
Definition. Given an open cover $S$ of a topological space $X$, the nerve of the cover $S$ is a simplicial complex with:
- vertices corresponding to the elements of the cover and
- $n$-simplices corresponding to non-empty intersection of $n$ elements of the cover.
In other words, the abstract simplicial complex $L$ is defined on the set $S$ by:
- $σ∈L$ if $σ = A_0A_1...A_n, A_0,A_1,...,A_n∈S,$ and
- $A_0 ∩ A_1 ∩ ... ∩ A_n ≠ ∅.$
Question: Suppose $L$ is created from an open cover of $|K|$ as above, then, is $L = K$?
Answer: No. Not in general.
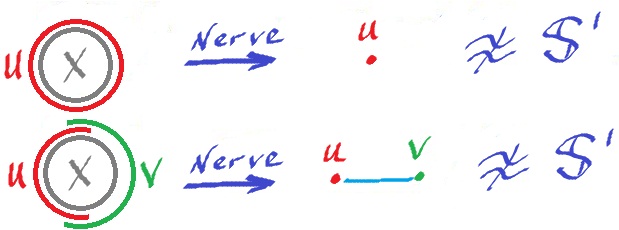
Examples below show what can go wrong, for the circle:
Exercise. Find more examples, both positive and negative.
What makes the difference? The elements of the cover, in the former case, or intersections of the elements, in the latter case, are topologically non-trivial.
Theorem 1 (Nerve Theorem). Let $K$ be a (finite) simplicial complex and $S$ an open cover of its realization $|K|$. Suppose the finite intersections of the elements of $S$ are contractible. Then the realization of the nerve of $S$ is homotopy equivalent to $|K|$.
This remarkable theorem establishes a direct link from discrete to continuous. Its proof can be found in Alexandroff and Hopf Topology. A simpler but even more important theorem is:
Theorem 1'. (Rotman, An Introduction to Algebraic Topology, p. 154) Let $K$ be a (finite) simplicial complex and $S$ an open cover of its realization $|K|$. Suppose the finite intersections of the elements of $S$ are acyclic. Then the realization of the nerve of $S$ has homology isomorphic to that of $|K|$.
The theorem about the reversed connection is more accessible.
Theorem 2. The nerve of the cover of a simplicial complex $K$ comprised of the stars of all vertices of of $K$ is an abstract simplicial complex isomorphic to $K$.
Proof. The proof follows the construction of the cover. First, list all the elements of the cover; they correspond to the vertices, trivially: $$St(A) <--> A.$$ Next look at their intersections. To get started, for 2-simplices: $$St(A) ∩ St(B) = \{σ∈K: A∈σ\} ∩ \{σ∈K: B∈σ\}$$ $$ = \{σ∈K: A∈σ, B∈σ\}.$$ This is non-empty iff K contains $AB$.
Fill in the details... (exercise). $\blacksquare$
Schematically, Theorem 2 can be interpreted as:
$\rightarrow$ open cover $S$ of $|K|$ $\rightarrow$ nerve $L$ of $S$
$\rightarrow$ simplicial complex $K$(the last arrow indicates an isomorphism).
Theorem 1 can be interpreted as:
$\rightarrow$ nerve $L$ of $S$ $\rightarrow$ realization $|L|$ of $L$
$\rightarrow$ topological space $X$(the last arrow indicates a homeomorphism). That's the way, ideally, the triangulation should work.
Exercise. Carry out this plan for: point, two points, figure eight, sphere, torus, Mobius band.
The examples and the theorems suggest that "refining" the open cover improves the chance that this plan will work. However, it can't work for some more complex spaces, with some infinity present.
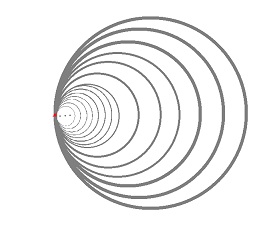
Example. Hawaiian earring is the subset of the plane that consists of infinitely many circles with just one point in common:
Let consider possible covers and their nerves. If we choose three open setts small enough, we can capture the first circle, and the second too, etc:
But there are infinitely many of them! Suppose one of the open sets, $W$, contains $(0,0)$. Then, for large enough $n$, $W$ will contain the $n$-th circle. Then this part of the nerve will look like this:
Therefore the topology of these smaller circles can't be captured, even if we are allowed to have infinitely many open sets.
Exercise. For a simplicial complex $K$ and a simplex $C$ in $K$ define the star of $C$ as the union of the interiors of all simplices in $K$ that contain $C$ (interior of a vertex = the vertex). Prove or disprove: The set of all stars in a finite complex form a basis of topology.
Exercise. Find an open cover of the sphere ${\bf S}^2$ the nerve of which is homeomorphic to ${\bf S}^2$. Solution.