This site is being phased out.
Sphere
The sphere is simply the set of points equidistant from a given point. The same exact approach can work in any dimension...
An $n$-dimensional sphere of radius $r$ centered at point $a$ is the set of points in ${\bf R}^{n+1}$ that lie at the distance of $r$ from point a:
$$\{x \in {\bf R}^{n+1}: ||x-a|| = r \}.$$
Exercise. What is a 0-sphere?
In topology we talk about the $n$-dimensional sphere denoted by ${\bf S}^n$. One can still think of it as the boundary of an $(n+1)$-dimensional ball:
$${\bf S}^n = \partial {\bf B}^{n+1}.$$
As a cell complex
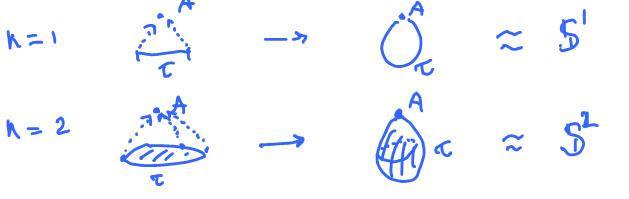
The $n$-sphere can be build as a cell complex from just two cells: a $0$-cell and a $n$-cell.
Exercise. Find other representations of the $n$-sphere as a cell complex?
Exercise. What about a cubical complex?
See how the sphere can be represented as a parametric surface.
Volume
Calculate
$$I = \int_D ( 1 - x^2 - y^2 )^{\frac{1}{2}} dA,$$
where
$$D = \{ ( x, y ): x^2 + y^2 \leq 1 \}.$$
Then
$$z = ( 1 - x^2 - y^2 )^{\frac{1}{2}}$$
Use iterated integration. Then
$$I = \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} ( 1 - x^2 - y^2 )^{\frac{1}{2}} dy dx.$$
To evaluate
$$\int ( 1 - x^2 - y^2 )^{\frac{1}{2}} dy$$
we need trigonometric substitution. This means we have to carry out separate trigonometric substitution for each $x$. Instead we do trigonometric" substitution for $( x, y )$ which turns into the "change of variables" and the new variable are the polar coordinates:
$$( x, y ) \rightarrow ( r, \theta ) $$
$$x = r \cos \theta \longleftrightarrow r = ( x^2 - y^2 )^{\frac{1}{2}}$$
$$y = r \sin \theta \longleftrightarrow \theta = \arctan \frac{y}{x}.$$