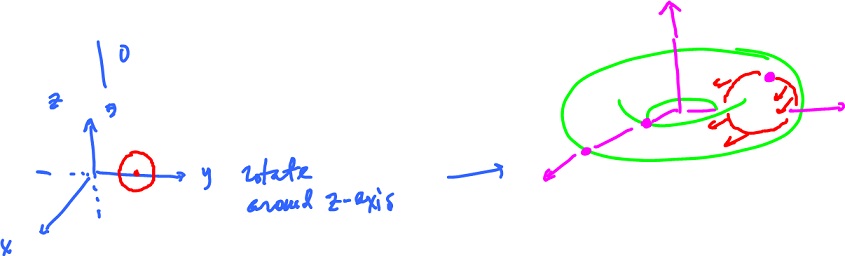This site is being phased out.
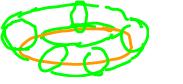
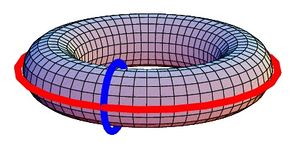
Torus

It a tire. Don't confuse with the donut - no air (void) inside.
Contents
As a product space
Both copies of ${\bf S}^1$ lie in ${\bf R}^2$, so the product would lie in ${\bf R}^4$. One, however, might think of small circles attached, vertically, to each point of the large circle on the plane.
Building a torus this way is a stretch - the way they are constructed will result in "a bag of points". That's where product topology comes into play.
As a quotient space and a cell complex
This is how it is constructed as a cell complex.
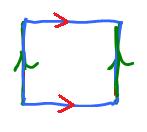
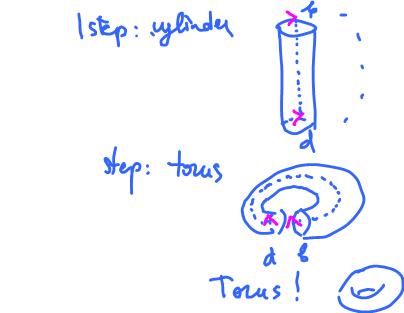
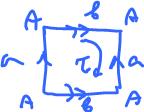
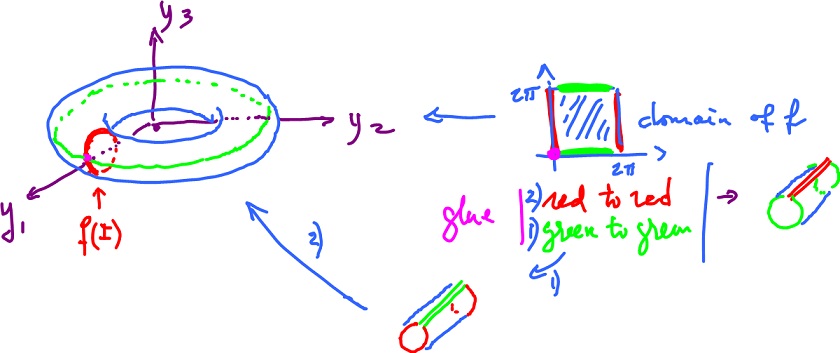
One can get the torus ${\bf T}^2$ from the cylinder by gluing the top to the bottom (the red arrows):
$$(x,0) \sim (x,1).$$
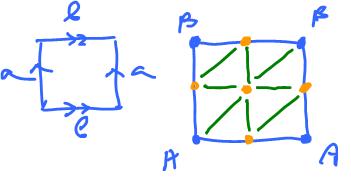
Or directly from the square:
See Quotient spaces.
Torus is a surface, i.e., it's locally homeomorphic to the plane.
Represent the torus as a simplicial complex (i.e., its triangulation):
The Euler characteristic is
$$\chi(T^2) = 1 - 2 + 1 = 0.$$
The $n$-torus, $T^n$, is an orientable $n$-dimensional manifold defined as the product of $n$ 1-spheres $$T^n = \underbrace{ S^{1} \times \cdots \times S^{1}}_{n},$$ or as a quotient space (exercise).
Homology
Compute its homology as a vector space:
$B_1(K)$ $= {\hspace{3pt} span}\{ \partial \tau \} = {\hspace{3pt} span}\{a + b - a - b \} = {\hspace{3pt} span}\{0 \} = 0,$ so
$H_1(K)$ $= {\hspace{3pt} span}\{a, b \} / 0 = {\hspace{3pt} span}\{a, b \}.$In particular, the the first Betti number is $2$.
The homology over ${\bf R}$
$${\bf R}, {\bf R}^2, {\bf R}, 0, \ldots$$
does not distinguish the torus from the Klein bottle, but the homology over ${\bf Z}$ does (see Homology as a group).
The torus is an orientable surface as it does not contain the Mobius band.
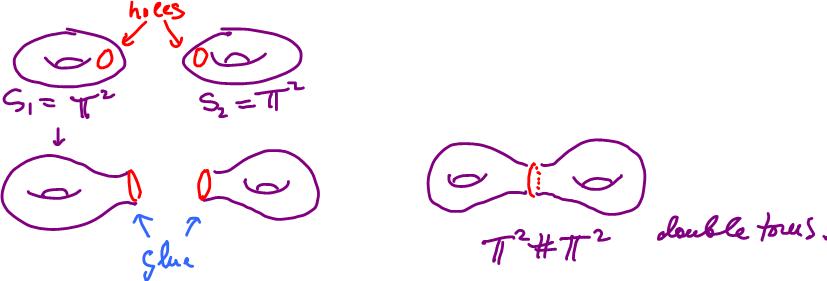
One can create the double torus by attaching two tori to each other in this fashion (connected sum).
As a parametric surface
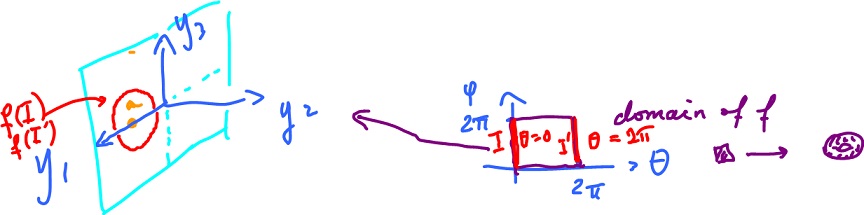
Torus is a surface in space given parametrically by the formula:
Domain: ${\theta} {\in} [ 0, 2 {\pi} ), {\varphi} {\in} [ 0, 2 {\pi} ]$.
We can think of it as a "parametric surface". Indeed we rotate a circle (off center) in the $yz$-plane around the $z$-axis:
Let's explain where this construction comes from. Consider the formula again:
$$f( {\theta}, {\varphi} ) = ( ( a + b \cos {\varphi} ) \cos {\theta}, ( a + b \cos {\varphi} ) \sin {\theta}, b \sin {\varphi} ).$$
1. Fix ${\theta} = 0$, find the image with one parameter (parametric curve).
$$\begin{array}{} f( 0, {\varphi} ) &= ( ( a + b \cos {\varphi} ) \cos 0, ( a + b \cos {\varphi} ) \sin 0, b \sin {\varphi} ) &= ( a + b \cos {\varphi}, 0, b \sin {\varphi} ) &= ( a, 0, 0 ) + b ( \cos {\varphi}, 0 \sin {\varphi} ). \end{array}$$
What is it? A circle in the $y_1y_3$-plane with center $( a, 0, 0 )$ and radius $b$. Fix ${\theta} = 2{\pi}$, find the image.
$$\begin{array}{} f( 0, {\varphi} ) &= ( ( a + b \cos {\varphi} ) \cos 2{\pi}, ( a + b \cos {\varphi} ) \sin 2{\pi}, b \sin {\varphi} ) \\ &= ( a + b \cos {\varphi}, 0, b \sin {\varphi} ), \end{array}$$
no change to previous calculation as $2{\pi}$ is the period of the $\sin$ and the $\cos$.
2. Fix ${\varphi} = 0$, find the image with one parameter.
$$\begin{array}{} f( {\theta}, 0 ) &= ( ( a + b \cos 0 ) \cos {\theta}, ( a + b \cos 0 ) \sin {\theta}, b \sin 0 ) \\ &= ( ( a + b ) \cos {\theta}, ( a + b ) \sin {\theta}, 0 ). \end{array}$$
What is it? A circle in the $y_1y_2$-plane with center $( 0, 0, 0 )$ and radius $( a + b )$.
To put this together: