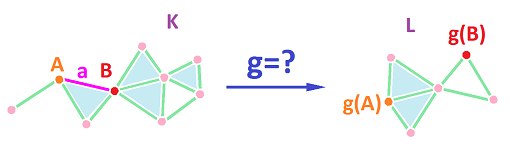This site is being phased out.
Triangulations
Contents
Simplicial vs cell complexes
Let's compare:
- simplicial complexes: cells are homeomorphic to points, segments, triangles, tetrahedra, ..., $n$-simplices;
- cell complexes: cells are homeomorphic to points, closed segments, disks, balls, ..., closed $n$-balls.
Since these are homeomorphic, the difference lies elsewhere.
Note: The cells in a cubical complex may be thought of as open, i.e., homeomorphic to open balls, while the cells in cell (and simplicial) complexes are closed, i.e., homeomorphic to closed balls. The reason is that a cubical complex may be built as the union of a collection of subsets of a Euclidean space, while a cell complex is built via the quotient construction, which always requires some points to be shared.
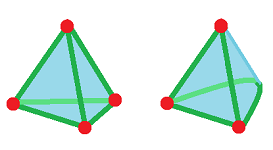
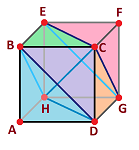
As we know, simplicial complexes are cell complexes with certain restrictions on their cells and the cells' faces. Recall that an $n$-simplex $\tau$ in a simplicial complex $K$ has $n+1$ faces, $\sigma < \tau$, each of which is an $(n-1)$-simplex, illustrated on the left:
This is why, for a cell complex to be a simplicial complex, it has to satisfy the following:
To see how this condition may be violated, consider the cell complex on the right and simply count the boundary cells:
- the $3$-cell has only $3$ faces;
- the bottom $2$-cell has only $2$ edges.
In addition, consider the simplest cell complex representation of the circle (one $0$-cell and one $1$-cell), below. The $1$-cell has only one end-point:
This isn't the only way things can go wrong though. If we add an extra vertex that cuts the $1$-cell in two, the above condition is satisfied. However, this still isn't a simplicial complex, since the two new cells share two end-points. In other words, two vertices $A,B$ are connected by two distinct edges: $AB \ne AB$. Finally, cutting one of the edges one more time produces a familiar simplicial complex.
Any cell complex can be turned into a simplicial complex in this fashion. The construction is called subdivision, i.e., cutting the cells into smaller cells until certain conditions are satisfied.
Theorem. A cell complex $K$ is a simplicial complex if for each of its cells $\tau \in K$, there is such a homeomorphism $h_{\tau}:\tau \to S_{\tau}$ of $\tau$ to a geometric simplex $S_{\tau}$ that
- (1) the complex contains all faces of each simplex:
$$\tau \in K, s < S_{\tau} \Rightarrow h_{\tau}^{-1}(s) \in K,$$
- (2) two simplices can only share a single face:
$$\tau, \sigma \in K \Rightarrow h_{\tau}(\tau \cap \sigma) < h_{\tau}(\tau).$$
Sidenote: The subdivision procedure is reminiscent of the subdivision of intervals in the definition of the definite integral via the Riemann sums.
Definition. A representation of a cell complex as a simplicial complex ($|K|\approx |K'|$) is called its triangulation.
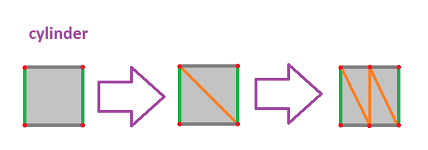
Example (cylinder). The familiar representation of the cylinder isn't a triangulation simply because the $2$-cell is a square not a triangle.
As we see, cutting it in half diagonally doesn't make it a triangulation because there is an edge still glued to itself. Adding more edges does the job.
$\square$
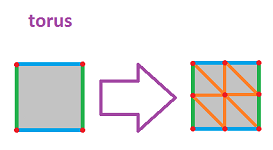
Example. A triangulation of the torus is given:
$\square$
Exercise. Find a triangulation for the rest of the six main surfaces.
Of course, a given cell complex can have many triangulations. In particular, any further subdivision of the above simplicial complexes will be a triangulation. The complexes that appear aren't isomorphic: there is no bijective simplicial map between them.
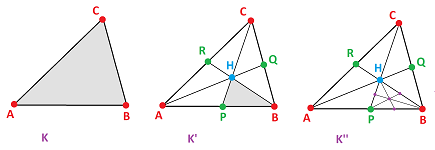
Instead of this ad hoc way of discovering triangulations, we can apply a method that always works. This method is a generalization of the barycentric subdivision that is applicable to cell complexes. First, we want to cut every $n$-cell into a collection of $n$-simplices. For each cell $\tau \in K$,
- we remove $\tau$ and all of its boundary cells (except for the vertices) from $K$;
- we add a vertex $V_{\tau}$ to $K$, and then
- we create the new cells spanned by $V_{\tau}$ and each boundary cell $a$ of $\tau$.
The result is a new cell complex $K'$.
If we ignore possible identifications between the boundary cells of $ABC$ in the complex $K$, it would have the structure of a simplicial complex. However, it is possible that this new triangular cell is attached to itself in the original complex $K$; for example, it's possible that $P=Q$. In that case, we have two edges, $PH=PQ$, connecting the same two vertices. The second barycentric subdivision $K' '$ (of all cells) solves this problem.
Exercise. (a) List the simplices in the above triangulation of the cube. (b) Provide a sketch and the list of the simplices for the triangulation that starts with adding a vertex in the middle of the cube.
As we have seen, cell complexes provide more economical (with fewer cells) representations of familiar objects than simplicial complexes. Therefore, if we need to compute the homology of a specific cell complex, we would never try to triangulate it. However, simplicial complexes are simpler in the way the cells are attached to each other. In fact, every simplex is just a list of its vertices. As a result, the proofs are simpler too.
Representation of a topological space as a realization of a simplicial complex is also called a triangulation. Triangulable spaces are called polyhedra. Since we assumed that all our simplicial complexes are finite, all polyhedra are assumed to the compact.
Triangulations of topological spaces
Cell complexes are compact representations of topological spaces, convenient for computing homology. But how do you find this representation if we don't even have a cell complex but only a topological space, i.e., a set with a collection of open subsets? What topological spaces are polyhedra?
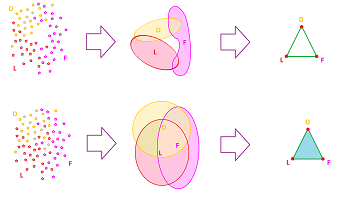
Example (garden). Let's recall how, in the very beginning of the book, we were able to understand the layout of a field of flowers of three kinds, say, D, L, and F, based only on the smells. The conclusion was, if we can detect only the three types, each of the three pairs, and no triples, then there must be a bare patch.
In other words, the homology of the field is that of the circle.
$\square$
The implicit assumptions that make this work are:
- the patches cover the whole field,
- the patches are open, and
- the patches and their intersections are acyclic.
With that idea in mind, let's study of the topology of realizations of simplicial complexes:
The topology of a realization $|K|$ of such a complex $K$ comes from the topology of each simplex modulo the gluing procedure. What makes each complex special is the way the simplices are attached to each other. Indeed, in a simplicial complex, the gluing never affects the topology of the simplex itself.
In particular, every point in an open cell has a Euclidean neighborhood relative to that cell. In other words, we have the following:
Proposition. For every point $A\in \dot{\sigma}$ with $\dim \sigma =n$, there is a neighborhood $B_A$ relative to $\sigma$ such that $B_A \approx {\bf R}^n$.
Beyond the interior of a simplex, the neighborhoods are more complex but still made of the Euclidean neighborhoods of the adjacent cells. But what if we aren't interested in these “small” open sets but in “large” open sets? We choose the latter to be unions of the interiors of simplices:
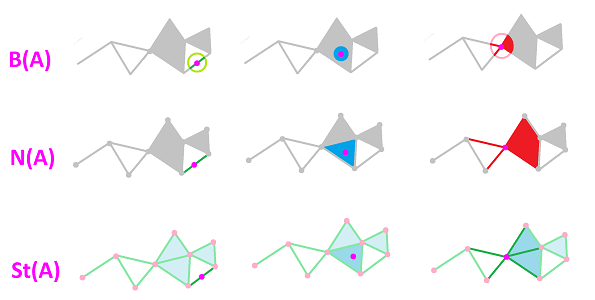
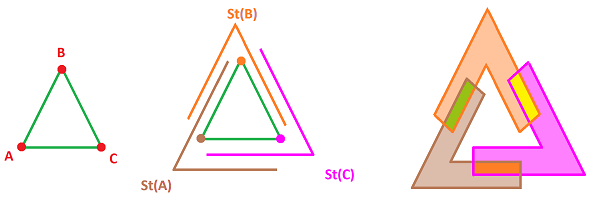
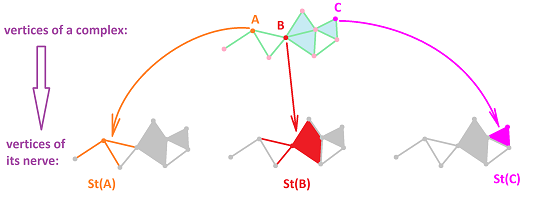
Definition. Given a simplicial complex $K$ and a vertex $A$ in $K$, the star of $A$ in $K$ is the collection of all simplices in $K$ that contain $A$: $${\rm St}_A ={\rm St}_AK := \{ \sigma \in K: A\in\sigma\}.$$ The open star is the union of the insides of all these cells: $$N_A =N_AK := \bigcup\{\dot{\sigma}: \sigma\in {\rm St}_A\}.$$ (Remember, $\dot{A}=A$.) Here, $K$ can be also any collection of simplices in a simplicial complex.
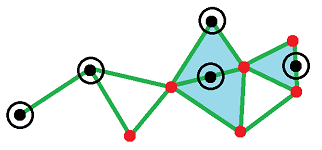
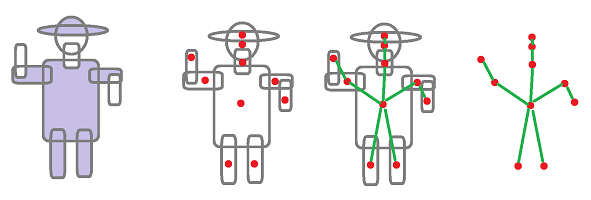
Exercise. The star of any point in $|K|$ is defined the same way. Sketch the stars of the circled points in the image below:
Exercise. If we add to ${\rm St}_A$ the boundary cells of all of its elements, the result is a simplicial complex, which may be called a “closed star”. Prove that it is acyclic.
Even though an open cell is open in its closed cell, it doesn't have to be open in $|K|$. We can see that in the above examples. We can't then jump to the conclusion that the open star $N_A$ is open. But it is.
Theorem. $N_A$ is an open subset of $|K|$ for any vertex $A$ in $K$.
Proof. The complement of the open star is the union of finitely many closed cells. Indeed: $$K \setminus {\rm St}_A = \{ \sigma \in K: A\not\in\sigma\}.$$ Therefore, $$|K| \setminus N_A = \bigcup\{\sigma: \sigma\not\in {\rm St}_A\}.$$ But closed cells are closed as continuous images of compact spaces. Therefore, the complement is closed. $\blacksquare$
In other words, $N_A$ is a neighborhood of $A$, which justifies the notation.
Note: The result would hold even if $K$ wasn't finite (such as ${\mathbb R}$), provided an infinite cell complex is properly defined. In fact, the above statement can be taken as a part of the definition of the topology of $|K|$.
This is the key step.
Corollary. $\{ N_A: A\in K^{(0)} \}$ is an open cover of $|K|$.
Now, we want to learn how construct a simplicial complex from this open cover of $|K|$, and do it in such a way that the result is the same as the original complex $K$. Keep in mind that in its realization the structure of the simplicial complex is lost, as in the image below, which is homeomorphic to the one above.
The example below suggests a way to approach the problem.
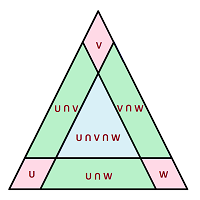
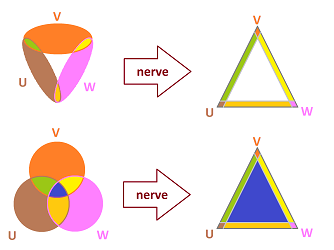
Example (circle). Let's consider the circle as a simple enough example. We start with the simplest triangulation of the circle -- a simplicial complex $K$ with three edges and three vertices. Then the stars of vertices consist of two edges each. It's an open cover.
Now, suppose $X$ is the (topological) circle. A homeomorphism of $|K|$ and $X$ creates an open cover of $X$ that consists of three overlapping open arcs:
Let $\gamma := \{U,V,W\}$ be this open cover of $X$. These sets came from the stars of the three vertices of $K$: ${\rm St}_A, {\rm St}_A, {\rm St}_A$, respectively. The cover seems vaguely circular, but how do we detect that by simply looking at the data?
The sets are now devoid of all geometry or topology. Therefore, the only thing they may have in common is their intersections.
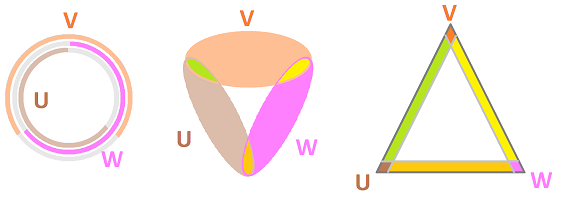
Let's make this more specific. These open sets have non-empty pairwise intersections but the only triple intersection is empty. Why is this important? Notice the pattern:
- $U \cap V \ne \emptyset \ \leftrightarrow\ N_A \cap N_B \ne \emptyset \ \leftrightarrow\ A, B$ are connected by an edge;
- $V \cap W \ne \emptyset \ \leftrightarrow\ N_B \cap N_C \ne \emptyset \ \leftrightarrow\ B, C$ are connected by an edge;
- $W \cap U \ne \emptyset \ \leftrightarrow\ N_C \cap N_A \ne \emptyset \ \leftrightarrow\ C, A$ are connected by an edge;
- $U \cap V \cap W = \emptyset \ \leftrightarrow\ N_A \cap N_B \cap N_C = \emptyset \ \leftrightarrow\ A, B, C$ are not connected by a face.
Following this insight, we forget for now about complex $K$ and create a new simplicial complex $L$ based entirely on how the elements of this cover $\gamma$ intersect.
We let $$L:= \{ U,V,W \}.$$ These are the vertices of complex $L$. The $1$-simplices of $L$ come from the following rule: for every pair $G,H\in \gamma$, $$GH\in K \Leftrightarrow G \cap H \ne \emptyset.$$
Further, the $2$-simplices of $L$ come from the following rule: for every triple $G,H,J\in \gamma$, $$GHJ\in K \Leftrightarrow G \cap H \cap J\ne \emptyset.$$ There aren't any.
We ended where we started! Indeed, $L$ is isomorphic to $K$.
$\square$
Example. This construction applied to the solid triangle is illustrated below:
$\square$
Exercise. Carry out this construction for spaces representing the letters: C, H, P, T.
We can now follow this logic to create simplicial complexes from any open cover of any topological space. But, since the word “skeleton” is already taken, we have to use “nerve” to name the output of this construction:
Definition. Given any collection of subsets $\alpha$ of a set $X$, the nerve of $\alpha$ is a simplicial complex $N_{\alpha}$ with:
- vertices corresponding to the elements of the cover, and
- $n$-simplices corresponding to non-empty intersection of $n+1$ elements of the cover.
In other words, the abstract simplicial complex $N_{\gamma}$ is defined on the set $\alpha$ by the rule: given $A_0,A_1,...,A_n \in \alpha$, $$\sigma = A_0A_1...A_n\in N_{\alpha} \text{ iff } A_0 \cap A_1 \cap \ ... \ \cap A_n \ne \emptyset.$$ We will also refer to the realization of $N_{\alpha}$ as the nerve.
Properties of the nerve
Theorem (Star Lemma). Suppose $A_0,A_1,...,A_n$ are vertices in complex $K$. Then these vertices form a simplex $$\sigma =A_0A_1 ... A_n$$ in $K$ if and only if $$\bigcap _{k=0}^n N_{A_k} \ne \emptyset.$$
Proof. To get started, for $2$-simplices we have: $$N_A \cap N_A = \{\sigma\in K: A\in\sigma\} \cap \{\sigma\in K: B\in\sigma\}$$ $$ = \{\sigma\in K: A\in\sigma, B\in\sigma\}.$$ This is non-empty if and only if $K$ contains $AB$.
$\blacksquare$
Exercise. Provide the rest of the proof.
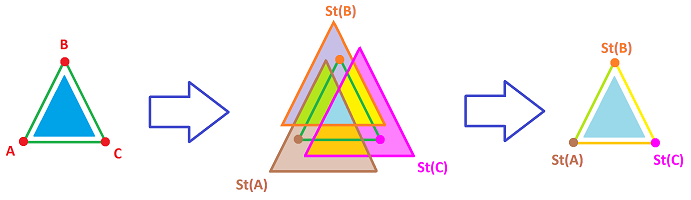
The building of the simplicial complex of the nerve is captured by this “nerve map”:
Theorem. The nerve $N$ of the cover of a simplicial complex $K$ that is comprised of the stars of all vertices of $K$ is an abstract simplicial complex isomorphic to $K$ via the simplicial map $h:K\to N$ defined by: $$h(A):=\operatorname{St}_A.$$
Proof. We follow the construction of the cover. First, list all the elements of the cover; they correspond to the vertices trivially: $$\operatorname{St}_A \leftrightarrow A.$$ The rest follows from the lemma. $\blacksquare$
Exercise. Is the nerve of a cubical complex a cubical complex?
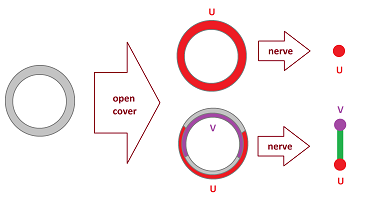
The examples demonstrate that the realization of the nerve of a cover doesn't have to be homeomorphic to the space: $$N_{\alpha}\not\approx X,$$ but maybe their homology groups coincide: $$H(N_{\alpha})\cong H(X)?$$ We have some examples to support this idea:
The complexes are, respectively, for the circle and the disk: $$\{U,V,W,UV,VW,WU\},\{U,V,W,UV,VW,WU,UVW\},$$ and their homology groups match those of the original spaces. Examples below show what can go wrong, for the circle:
The complexes are, respectively: $$\{U\},\{U,V,UV\},$$ and their homology groups don't match those of the circle.
Exercise. Find more examples, both positive and negative.
What makes the difference for the last two examples?
In the first example, the only element of the cover isn't homeomorphic to the segment as one would expect, but to the circle. In the second example, the two elements of the cover are homeomorphic to the segment but their intersection isn't as it's not path-connected. In either case, the issue is the topological non-triviality of these sets.
Example. Consider the cover of the sphere ${\bf S}^2$ by two open sets obtained by removing the north pole and then the south pole: $$\alpha := \{ {\bf S}^2 \setminus \{N\},{\bf S}^2 \setminus \{S\}\}.$$
The issue is resolved by the following theorem that we will accept without proof (see Rotman, An Introduction to Algebraic Topology, p. 154).
Theorem (Nerve Theorem). Let $K$ be a (finite) simplicial complex and $\alpha$ is a cover of $|K|$ that consists of the closed stars of its barycentric subdivision. Suppose the finite intersections of the elements of $\alpha$ are acyclic. Then the realization of the nerve of $\alpha$ has homology isomorphic to that of $K$: $$H(N_{\alpha}) \cong H(K).$$
Exercise. Prove the claim about the homology of the flower field in the above example.
Exercise. Find an example of a complex for which the conclusion of the theorem fails because the triple intersections aren't acyclic.
Either of these two theorems can be seen as a sequence of transitions that ends where it starts. We represent them schematically:
This is the way, ideally, the triangulation is supposed work.
Exercise. Test this plan for: a point, two points, figure eight, the sphere, the torus, the Mobius band.
The examples and the theorems suggest that “refining” the open cover improves the chance that this plan will work. However, nothing will help the spaces that can't be represented as realizations of finite complexes.
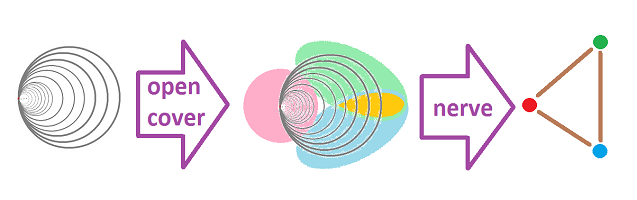
Example (Hawaiian earring). Recall that the Hawaiian earring is the subset of the plane that consists of infinitely many circles with just one point in common: $n$th circle is centered at $(1/n,0)$ with radius $1/n$, $n=1,2,3,...$.
Let's consider possible covers and their nerves. If we choose three open sets small enough, we can capture the first circle:
We can also get the second too, with smaller open sets. But there are infinitely many of them! In general, suppose one of the open sets, $W$, contains $(0,0)$. Then, for large enough $N$, $W$ will contain every $n$th circle with $n > N$. Therefore the holes in these smaller circles can't be captured.
This failure to triangulate is not caused by having infinitely many circles. Compare this space to the same set with an alternative topology. This alternative, the “bouquet of circles” ${\bf R} / {\bf Z}$, can be easily triangulated if we are allowed to use infinitely many simplices. This is a rare example when the Euclidean topology produces results more pathological than something else.
$\square$
Example. An attempt to triangulate the punctured disk, ${\bf B}^2 \setminus \{(0,1)\}$, will cause a similar problem:
$\square$
Exercise. For a simplicial complex $K$ and a simplex $C$ in $K$ define the star of $C$ as the union of the interiors of all simplices in $K$ that contain $C$. Prove or disprove: The set of all stars in a finite complex form a basis of topology.
Exercise. Find an open cover of the sphere ${\bf S}^2$ the nerve of which is homeomorphic to ${\bf S}^2$.
Social choice: ranking
Here, we will consider the topology of the space of choices. We start with a simple setting of ranking, i.e., ordering multiple alternatives. The alternatives may be candidates running for elections, movie recommendations, and other votes of personal preferences.
Suppose the number $n$ of alternatives/candidates is fixed: $$A=A_n:=\{1,2,...,n\}.$$ Each of the voter's $x$ preference of alternative $j\in A$ over alternative $i\in A$ is expressed as follows: $$i <_x j.$$ Then the complete vote of $x$' is a (strict) ordering of the alternatives. It may look like this: $$1 <_x 2 <_x 3 <_x... <_x n.$$ The totality of all possible votes is the set of these orderings $$Z=Z_n:=\{(i_1,i_2 , ... ,i_n):\ i_k\in A_n,i_k\ne i_l\}.$$ It can be seen as the group structure of $\mathcal{S}_n$, the group of permutations of $n$ elements.
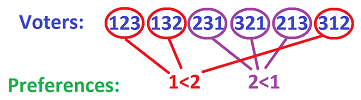
In particular, for $n=3$ there are $6$ orderings: $$Z_3=\{123,132,231,321,213,312\}.$$ This order of elements of $Z$ is completely arbitrary and so would be any other. Is there a meaningful way to arrange them on the plane? Maybe a circle?.. What we are looking for is a topology for $Z$!
To find an appropriate one, we start with an observation. Let's fix two alternatives $i,j\in A,\ i < j$, and note that if voter $x$ votes $i <_x j$, then we expect a “close enough” to $x$ voter $y$ to also choose $i <_y j$. We write: $$i <_x j \Longrightarrow i <_y j.$$ This is just a way to informally express the idea that voting preferences should vary from person to person in a continuous fashion. The aggregate of all choices is then a continuous function $F$ from the space of voters to the space of pairwise preferences. Initially, we will assume that there is exactly one voter for each ordering so that the space of voters is $Z$, with the topology we are to choose. Then we have $$F:Z\to Y:=\{(i,j),(j,i)\}.$$
For $n=3$, this function is illustrated below:
Since $Y$ is discrete, the points in this space are open and, therefore, the preimages of points under $F$ are open too. There are only two: $$U_{ij}:=F^{-1}((i,j))=\{x\in Z: \ i<_x j\},$$ $$U_{ji}:=F^{-1}((j,i))=\{x\in Z: \ j<_x i\}.$$ The complexity of this setup comes from the fact that there are many pairs $(i,j),\ i<j$, each of them produces such a pair of sets, and either of these sets is supposed to be open:
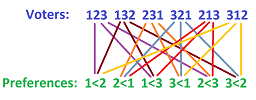
We pool this information by considering all the pairwise rankings $$\alpha := \{U_{ij}:\ i,j\in A,i\ne j\}$$ as an open cover of $Z$.
Exercise. Sketch $\alpha$ for $n=3$.
Exercise. Describe the basis of neighborhoods of this topology by taking finite intersections of the elements of $\alpha$ (that's why $\alpha$ is called a “pre-basis”).
Definition. For a given $n$, the nerve $R_n:=N_{\alpha}$ of the cover $\alpha$ of pairwise rankings is a simplicial complex called the complex of orderings (or complex of rankings).
Example. For $n=2$, there are only two choices and only two orderings, each an open set: $$\{12\}=U_{12},\ \{21\}=U_{21}.$$ They don't intersect. Therefore, $$R_2=N_{\alpha}=\{U_{12},U_{21}\}$$ is the complex of two disconnected vertices.
$\square$
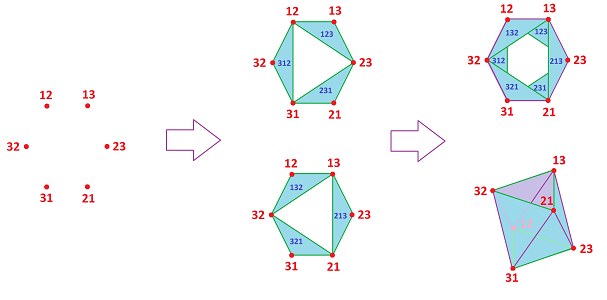
Example. For $n=3$, we have $$Z_3=\{123,132,231,321,213,312\}.$$ The cover $\alpha$ consist of $6$ stars of these sets: $$U_{12}=\{123,132,312 \},\ U_{21}=\{213,231,321 \},$$ $$U_{23}=\{231,213,123 \},\ U_{32}=\{321,312,132 \},$$ $$U_{13}=\{132,123,213 \},\ U_{31}=\{312,321,231 \}.$$ These are the vertices of the nerve $N_{\alpha}$ and they are marked below with simply "$12$","$21$", etc.:
Then, we add faces to the complex $R_3=N_{\alpha}$ by following this idea: are there any voters who vote simultaneously $1<2, 1<3, 2<3$? Yes, they vote: $1<2<3$. Thus, we have a $2$-simplex $123$ connecting vertices $12,13,23$. However, are there any voters who vote simultaneously $1<2, 2<3, 3<1$? No, because this would be a circular, impossible vote: $1<2<3<1$! Then, there is no $2$-simplex connecting vertices $12,13,23$. The end result is an octahedron with two, opposite to each other, faces missing.
$\square$
Exercise. Sketch a star of $R_4$.
Notice that that while we've built simplicial complexes from data before, it is very different this time. Even though it is the orderings we care about, we didn't make them the vertices, as usual, of the complex but rather its simplices, of the highest dimension!
Let's summarize that we know so far.
Theorem.
- (1) The simplices of highest dimension of $N_{\alpha}$ correspond to the orderings, i.e., the elements of $Z$.
- (2) The complex $R_n=N_{\alpha}$ is the union of these simplices (as subcomplexes of the simplex of all possible votes).
- (3) The dimension of this complex is
$$\dim R_n =\frac{(n-2)(n+1)}{2}.$$
Proof. (3) Let's first observe that, since there are only $n$ alternatives, there are at most $$\frac{n(n-1)}{2}$$ pairwise combinations with no repetitions, unless we reverse the order. Now, suppose there is a simplex $\sigma$ of dimension $$\dim \sigma = \frac{(n-2)(n+1)}{2}+1 = \frac{n(n-1)}{2}.$$ This means that $\sigma$ has more vertices than available pairs. Therefore, there are at least two vertices of $\sigma$ that are marked with the same pair of alternatives but reversed: $ij$ and $ji$. Such a simplex would represent an impossible vote! That contradicts the way $R_n$ is constructed. $\blacksquare$
Exercise. Prove parts (1) and (2).
One can guess that $$H_1(R_3)={\bf Z}.$$
Exercise. Prove this statement by a direct computation.
We have a more general result:
Theorem. The homology of the complex of orderings of $n$ elements is that of the $(n-2)$-sphere: $$H(R_n)=H({\bf S}^{n-2}).$$
The idea of the proof is to find a familiar space and then show that it has an open cover with the nerve isomorphic to $R_n=N_{\alpha}$. We choose as such space the $n$-dimensional Euclidean space with the diagonal cut out: $$M := {\bf R}^n \setminus \Delta,$$ where $$\Delta :=\{(u_1,...,u_n)\in {\bf R}^n:\ u_i = u_j\}.$$ It is illustrated below for dimension $3$:
Consider the cover of $M$ $$\beta := \{ {\bf R}^n_{ij}:\ 1\le i \ne j \le n \}$$ that consists of all half-spaces: $${\bf R}^n_{ij}:=\{ (u_1,...,u_n)\in {\bf R}^n:\ u_i < u_j \}.$$
Exercise. Prove that $$N_{\beta} \cong N_{\alpha},$$ and then finish the proof of the theorem by applying the Nerve Theorem from the last subsection.
The Simplicial Extension Theorem
Recall that a simplicial map $$g:K\to L$$ is fully determined by its values on the vertices: $$g:K^{(0)} \to L^{(0)}.$$ How do we extend $g$ to $1$-simplices of $K$? If $AB\in K$, where $A,B$ are vertices in $K$, then we set: $$g(AB):=g(A)g(B).$$ We just need to make sure that there is an edge between $g(A)$ and $g(B)$:
We have to require that
- $A$ and $B$ are adjacent in $K$ if and only if $g(A)$ and $g(B)$ are adjacent in $L$.
If we understand “adjacent” as “close”, this condition mimics continuity as seen below.
For the higher dimensions, we set: $$g(A_0 ... A_n) := g(A_0) ... g(A_n),$$ with possible repetitions. The new map, $$g:K\to L,$$ given by this formula is called the simplicial extension of $g$.
Proposition. Given a map $g:K^{(0)} \to L^{(0)}$ of vertices of two simplicial complexes. Then its simplicial extension is well-defined provided: $$A_0 ... A_n \in K \Longrightarrow g(A_0) ... g(A_n) \in L$$ (vertices may appear more than once).
A more subtle way to verify this condition follows from the result below.
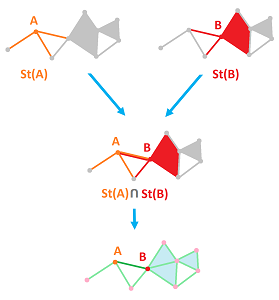
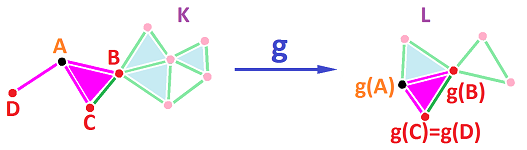
Theorem (Simplicial Extension Theorem). Suppose function $$f:|K| \to |L|$$ maps vertices to vertices: $$f(K^{(0)}) \subset L^{(0)}.$$ Then the simplicial extension $g$ of $f$ restricted to vertices, $f\big|_{K^{(0)}}$, is well-defined provided $$f(N_A)\subset N_{f(A)},$$ for every vertex $A$ in $K$.
Proof. The Star Lemma states that if we have a list, with possible repetitions, of vertices in a simplicial complex, then they form a simplex of the complex if and only if the intersection of the stars of all these vertices is non-empty. We use this fact for both $K$ and $L$ below.
Let $g$ be the restriction of $f$ to the vertices. By the proposition, we only need to prove that $$A_0 ... A_n \in K \Longrightarrow g(A_0) ... g(A_n)\in L.$$ Now, by the Star Lemma, this is equivalent to: $$\bigcap _{k=0}^n N_{A_k} \ne \emptyset \Longrightarrow \bigcap _{k=0}^n N_{f(A_k)} \ne \emptyset.$$ But, by the assumption, the image under $f$ of the set on the left is contained in the set on the right, as seen below: $$f \left( \bigcap _{k=0}^n N_{A_k} \right) \subset \bigcap _{k=0}^n f(N_{A_k}) \subset \bigcap _{k=0}^n N_{f(A_k)} .$$ $\blacksquare$
Exercise. Prove the inclusion used above, for any family of sets $\{S_{\alpha}\}$ and any function $f$: $$f \left( \bigcap _{\alpha} S_{\alpha} \right) \subset \bigcap _{\alpha} f(S_{\alpha}).$$
Corollary. A function $g:K\to L$ is a simplicial map if and only if it satisfies the following conditions, for every vertex $A$ in $K$,
- $g(A)$ is a vertex in $L$, and
- $g(\operatorname{St} _A)\subset \operatorname{St}_ {g(A)}.$
Exercise. Prove the corollary.