This site is being phased out.
Euler-Poincare formula
Redirect to:
The Euler characteristic of the sphere is $2$ (that's the Euler formula): $$\chi ({\bf S}^2) = 2.$$
Another topological invariant of the sphere is its set of the Betti numbers: $$\begin{array}{l} \beta_0({\bf S}^2) = 1, \\ \beta_1({\bf S}^2) = 0, \\ \beta_2({\bf S}^2) = 1, \\ \beta_3({\bf S}^2) = 0, {\rm \hspace{3pt} etc}. \end{array}$$
It's not a coincidence that the Betti numbers add up to $2$. But what about other complexes?
First, the point $P$: $$\chi(P) = 1 - 0 + 0 ... = 1,$$ $$\beta_0(P) = 1,$$ $$\beta_1(P) = 0, {\rm \hspace{3pt} etc.}$$
Once again, the Betti numbers add up to the Euler number.
Next, the circle $C$: $$\chi(C) = 1 - 1 + 0 ... = 0,$$ $$\beta_0(C) = 1,$$ $$\beta_1(C) = 1,$$ $$\beta_2(C) = 0.$$ Etc.
Turns out: just like the Euler characteristic is the alternating sum of the number of cells of each dimension, it might also be the alternating sum of the Betti numbers of each dimension: $$\chi(C) = \beta_0(C) - \beta_1(C) + \beta_2(C) - \ldots$$
The Betti numbers count the number of topological features, but formally the definition of the Betti numbers of complex $K$ is: $$\beta_k(K) = \dim H_k(K),$$ where $H_k(K)$ are the homology groups (vector spaces) of $K$ ($\dim$ replaced with rank in case of homology groups).
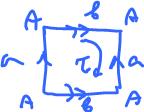
Consider the torus ${\bf T}^2$: $0$-cells: $1$, $1$-cells: $2$, $2$-cells: $1$, so $$\chi({\bf T}^2) = 1 - 2 + 1 = 0.$$
Because this cell complex representation is so efficient, each of the cells is also a basis element of the corresponding homology group: $$\begin{array}{l} H_0({\bf T}^2) = {\rm span}\{A\} &\rightarrow \beta_0({\bf T}^2) = 1, \\ H_1({\bf T}^2) = {\rm span}\{a,b\} &\rightarrow \beta_1({\bf T}^2) = 2, \\ H_2({\bf T}^2) = {\rm span}\{ \tau \} &\rightarrow \beta_2({\bf T}^2) = 1, \\ H_3({\bf T}^2) = 0 &\rightarrow \beta_3({\bf T}^2) = 0, {\rm \hspace{3pt} etc.} \end{array}$$
Since we are just counting the cells, it's no surprise that the formula holds: $$\chi({\bf T}^2) = \beta_0(C) - \beta_1(C) + \beta_2(C) - \ldots$$
We need to show that this still holds for all finite cell complexes.
Theorem (Euler-Poincaré formula). If $K$ is a finite cell complex then its Euler characteristic is equal to the alternating sum of the Betti numbers of each dimension: $$\chi(K) = \displaystyle\sum_k(-1)^k \beta_k(K).$$
Proof. Requires a couple of facts from linear algebra.
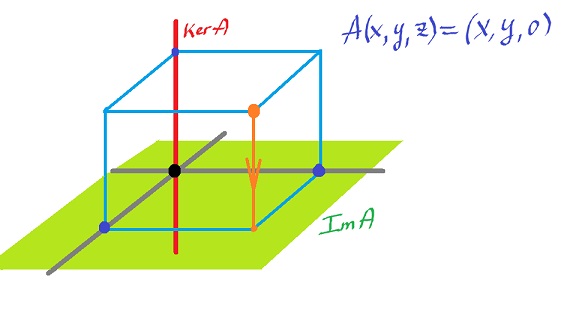
Fact 1. If $M, L$ are vector spaces and $A \colon M \rightarrow L$ is a linear operator, then
Fact 2. If $Y$ is a subspace of vector space $X$, then $$\dim X / Y = \dim X - \dim Y.$$
Now there are four vector spaces involved in the computation of the Betti numbers of $K$: the chain group, the cycle group, the boundary group, and the homology group. These are their dimensions: $$\begin{array}{l} c_k = \dim C_k(K),\\ z_k = \dim Z_k(K), \\ b_k = \dim B_k(K), \\ \beta_k = \dim H_k(K). \end{array}$$
Recall that for the boundary operator $$\partial_k \colon C_k(K) \rightarrow C_{k-1}(K), $$ we define $$Z_k(K) = \ker \partial_k,$$ and $$B_{k-1}(K) = \hspace{3pt} im \hspace{3pt} \partial_k.$$
Facts $1$ and $2$ imply as a corollary: $$\dim M - \dim \ker A = \dim im \hspace{3pt} A.$$
Applying this to the boundary operator above, we obtain: $$\dim C_k(K) - \dim ker \hspace{3pt} \partial_k = \dim im \hspace{3pt} \partial_k,$$ or:
Lemma 1. $$c_k - z_k = b_{k-1}.$$
Recall that $$H_k(K) = Z_k(K) / B_k(K).$$ Then, from Fact $2$, it follows
Lemma 2. $$\beta_k = z_k - b_k.$$
Finally, suppose $n$ is the highest dimension of a cell in $K$. Then $$\begin{array}{l} \beta_0 &- \beta_1 + \beta_2 - \ldots + (-1)^k \beta_n, {\rm \hspace{3pt} substitute \hspace{3pt} from \hspace{3pt} Lemma \hspace{3pt}}2 \\ &= (z_0 - b_0) - (z_1 - b_1) + (z_2 - b_2) - \ldots + (-1)^n(z_n - b_n) \\ &= z_0 - b_0 - z_1 + b_1 + z_2 - b_2 - \ldots + (-1)^n z_n - (-1)^n b_n, {\rm \hspace{3pt} substitute \hspace{3pt} from \hspace{3pt} Lemma \hspace{3pt}} 1 \\ &= z_0 - (c_1 - z_1) - z_1 + (c_2 - z_2) + z_2 - (c_3 - z_3) - \ldots + (-1)^n z_n - (-1)^n(c_{n+1} - z_{n+1}), {\rm \hspace{3pt} cancel \hspace{3pt}} z's \\ &= z_0 - c_1 + c_2 - c_3 - ... + (-1)^{n+1}c_{n+1} - (-1)^n z_{n+1} \\ &= c_0 - c_1 + c_2 - c_3 - \ldots + 0 - 0 \\ &= \chi(K). {\rm \hspace{3pt} \blacksquare} \end{array}$$