This site is being phased out.
Euler and Lefschetz numbers
Contents
The Euler characteristic
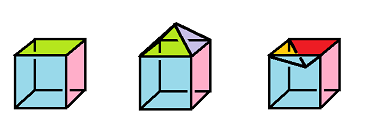
Recall the Euler formula for a convex polyhedron: $$\# {\rm vertices} - \# {\rm edges} + \# {\rm faces} = 2.$$
A remarkable result, especially when you realize that it has nothing to do with convexity! Indeed, we can simply turn protrusions into indentations without changing this number:
We already know, and will prove below, that the meaning of the formula is topological.
Definition. The Euler characteristic $\chi (K)$ of an $n$-dimensional cell complex $K$ is the alternating sum of the number of cells in $K$ for each dimension: $$\chi (K) = \# 0 \text{-cells} - \# 1\text{-cells} + \# 2\text{-cells} - ... \pm \# n\text{-cells}.$$
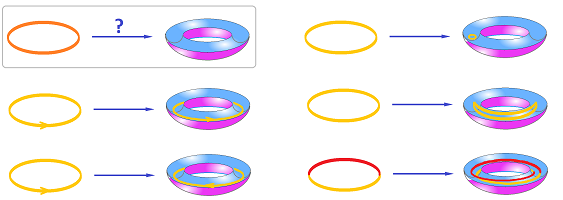
Exercise. Compute the Euler characteristic of the circle, the cylinder, the Mobius band, the torus, and the Klein bottle.
To reveal the topological nature of this number, we will need to link it to homology. This will require a more formal, algebraic approach which will prove to be very powerful when applied to the Euler characteristic and related concepts. In particular, counting cells in the definition is replaced with the following linear algebra.
Proposition. If $C_k(K)$ is the $k$-chain group of cell complex $K$, then $$\# k \text{-cells} = \dim C_k(K).$$ Consequently, $$\chi (K) = \sum_{k} (-1)^k \dim C_k(K).$$
We assume that all chains and homology below are over the reals.
We will need this well-known result.
Theorem (Inclusion-Exclusion Formula). For sets $A,B \subset X$, we have: $$\#(A \cup B) = \# A + \# B - \#(A \cap B).$$
It has an analogue for the Euler characteristic. But we need to apply this formula to bases of the vector spaces (rather than the cells).
Proposition. For two subspaces $U,V$ of a finitely dimensional vector spaces, we have $$\dim < U \cup V > = \dim U + \dim V - \dim U \cap V.$$
Exercise. Prove the proposition. Hint: $\dim W=\#$ basis of $W$.
Theorem (Inclusion-Exclusion Formula for Euler Characteristic). Suppose $K, L,$ and $K \cap L$ are subcomplexes of finite cell complex $K \cup L$, then $$\chi (K \cup L) = \chi (K) + \chi (L) - \chi (K \cap L).$$
Proof. By the above proposition, we have: $$\begin{array}{ccc} \dim < C_0(K) \cup C_0(L) > = \dim C_0(K) + \dim C_0(L) - \dim C_0(K) \cap C_0(L), \\ \dim < C_1(K) \cup C_1(L) > = \dim C_1(K) + \dim C_1(L) - \dim C_1(K) \cap C_1(L), \\ \vdots \\ \dim < C_n(K) \cup C_n(L) > = \dim C_n(K) + \dim C_n(L) - \dim C_n(K) \cap C_n(L). \\ \end{array}$$ Since for each $i=0,1,...,n$, we have $$\begin{array}{cccc} < C_i(K) \cup C_i(L) > & = C_i(K \cup L), \\ C_i(K) \cap C_i(L) & = C_i(K \cap L), \end{array}$$ the alternating sum of the above equations gives us the formula. $\blacksquare$
The Euler characteristic behaves well under products.
Theorem (Product Formula for Euler Characteristic). The Euler characteristic is multiplicative. For two finite cell complexes $K$ and $L$, we have: $$\chi (K \times L) = \chi (K) \cdot \chi(L).$$
Exercise. Prove the theorem. Hint: $\dim (U\oplus V)=\dim U + \dim V$.
Exercise. Compute the Euler characteristic of the $n$-dimensional torus ${\bf T}^n$.
The Euler-Poincaré Formula
The Euler characteristic of a cell complex is computed from: $$c_k(K) := \dim C_k(K).$$ These numbers resemble the Betti numbers of the cell complex: $$\beta_k(K) := \dim H_k(K).$$ What if we compute an alternating sum of the latter numbers rather than the former?
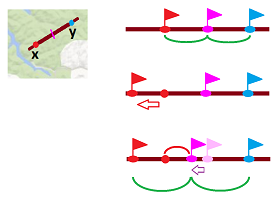
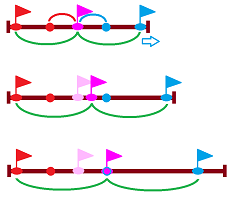
Implicitly, we have already done this, in the Euler formula. On the one hand, we have: $$\chi ({\bf S}^2) = 2,$$ which holds regardless of the triangulation. On the other, the alternating sum of the Betti numbers of the sphere $$\beta_0({\bf S}^2) = 1,\ \beta_1({\bf S}^2) = 0,\ \beta_2({\bf S}^2) = 1,\ \beta_3({\bf S}^2) = 0,...$$ also produces $2$!
Is this a coincidence? Let's check out other complexes.
Example (point). First, the point $P$: $$\begin{array}{llll} \chi(P) = 1 - 0 = 1,\\ \beta_0(P) - \beta_1(P) = 1-0=0. \end{array}$$ Once again, the Betti numbers add up to the Euler number.
Next, the circle $C$: $$\begin{array}{llll} \chi(C) = 1 - 1 + 0 = 0,\\ \beta_0(C) - \beta_1(C) +\beta_2(C) = 1-1+0= 0! \end{array}$$ $\square$
Example (torus). Consider the torus ${\bf T}^2$. We have:
- $0$-cells: $1$,
- $1$-cells: $2$,
- $2$-cells: $1$.
So, $$\chi({\bf T}^2) = 1 - 2 + 1 = 0.$$ Because this cell complex representation is so efficient, each of the cells also represents an element of a basis element of the corresponding homology group: $$\begin{array}{lll} H_0({\bf T}^2) = < A > & \Rightarrow \beta_0({\bf T}^2) = 1, \\ H_1({\bf T}^2) = < a,b > & \Rightarrow \beta_1({\bf T}^2) = 2, \\ H_2({\bf T}^2) = < \tau > & \Rightarrow \beta_2({\bf T}^2) = 1, \\ H_3({\bf T}^2) = 0 & \Rightarrow \beta_3({\bf T}^2) = 0. \end{array}$$ The formula holds: $$\chi({\bf T}^2) = \beta_0(C) - \beta_1(C) + \beta_2(C) - ...$$ $\square$
Since we are just counting the cells, it's no surprise that the formula holds. Of course, it will always hold when there is one cell per homology generator. We need to show that this formula holds for all cell complexes.
Theorem (Euler-Poincaré Formula). If $K$ is a finite cell complex, then its Euler characteristic is equal to the alternating sum of the Betti numbers of each dimension: $$\chi(K) = \displaystyle\sum_k(-1)^k \beta_k(K).$$
Proof. The proof will require a couple of facts from linear algebra.
Proposition.
- (1) If $M, L$ are vector spaces and $A: M \to L$ is a linear operator, then
$$M /\ker A \simeq \operatorname{Im} A.$$
- (2) If $Y$ is a subspace of vector space $X$, then
$$\dim X / Y = \dim X - \dim Y.$$
The proposition implies the following:
Corollary. If $M, L$ are vector spaces and $A: M \to L$ is a linear operator, then $$\dim M - \dim \ker A = \dim \operatorname{Im} A.$$
Now, there are four vector spaces involved in the computation of the Betti numbers of complex $K$, for each $k=0,1,2,...$: $$\begin{array}{lllll} \text{chain group: } & C_k , & c_k := \dim C_k;\\ \text{cycle group: } & Z_k = \ker \partial_k, & z_k := \dim Z_k;\\ \text{boundary group: } & B_k =\operatorname{Im} \partial_{k+1}, & b_k := \dim B_k;\\ \text{homology group: } & H_k = Z_k / B_k, & \beta_k := \dim H_k, \end{array}$$ where $$\partial_k : C_k \to C_{k-1} $$ is the boundary operator.
Applying the corollary to the boundary operator, we obtain: $$\dim C_k - \dim \ker \partial_k = \dim \operatorname{Im} \partial_k.$$ In other words, we have the following.
Lemma A. $c_k - z_k = b_{k-1}.$
Next, from part (2) of the proposition, we have the following.
Lemma B. $\beta_k = z_k - b_k.$
Finally, suppose $n$ is the highest dimension of a cell in $K$. Then the right-hand side of the formula is: $$\begin{array}{llllll} = &\beta_0 &- \beta_1 &+ \beta_2 - ... &+ (-1)^k \beta_n\\ &&&\text{ substitute from Lemma B} \\ = &(z_0 - b_0) &- (z_1 - b_1) &+(z_2 - b_2) -... &+ (-1)^n(z_n - b_n) \end{array}$$ $$\begin{array}{llllll} = &z_0 &- b_0 - z_1 &+b_1 +z_2 - ... &+ (-1)^n z_n - (-1)^n b_n\\ &&&\text{ substitute from Lemma A}\\ = &z_0 &- (c_1 - z_1) - z_1 &+ (c_2 - z_2) +z_2 + ... &+ (-1)^n z_n - (-1)^n(c_{n+1} - z_{n+1})\\ &&&\text{ cancel the z's} \\ = &z_0 &- c_1 &+ c_2 - ... & + (-1)^{n+1}c_{n+1} - (-1)^n z_{n+1} \\ = &c_0 &- c_1 &+ c_2 - ... &+ 0 &- 0 \\ = &\chi(K). \end{array}$$
$\blacksquare$
Exercise. Prove the propositions.
The invariance of homology then gives us the following.
Corollary. The Euler characteristic is a topological invariant of polyhedra.
Because so much information is lost, the Euler characteristic is poor man's homology; however, ...
Exercise. Under what circumstances can the homology of $X$ be derived from its Euler characteristic for (a) $X$ a graph, (b) $X$ a surface?
Fixed points
If you stretch a rubber band by moving one end to the right and the other to the left, some point of the band will end up in its original position:
And, it doesn't matter if the stretching isn't uniform or if there is some shrinking, or even folding! Such a point is called a fixed point of the transformation.
This problem is described mathematically as follows.
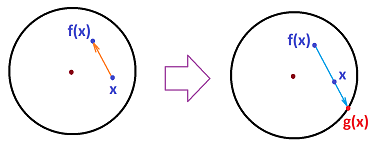
Fixed Point Problem. If $X$ is a topological space and $f:X \to X$ is a self-map, does $f$ have a fixed point: $x\in X$ such that $f(x)=x$?
The result above is, therefore, about a fixed point of a map $f:[a,b] \to [a,b]$.
Exercise. Prove this result by using the Intermediate Value Theorem.
Exercise. Demonstrate that both continuity of the map and the compactness of the interval are crucial.
Exercise. Under what circumstances is the set of fixed points closed?
A similar problem about stretching a disk or a ball requires more advanced techniques (to be proven later).
Theorem (Brouwer Fixed Point Theorem). Any map on a closed ball has a fixed point. In other words, if $f: {\bf B}^n\to {\bf B}^n$ is a map then there is $x\in {\bf B}^n$ such that $f(x)=x$.
An informal interpretation of the $2$-dimensional version of this theorem is: a crumpled copy of a page placed on it will have two identical words located one exactly over the other.
Exercise. Prove the theorem. Hint:
Of course, the theorem holds if the ball is replaced with anything homeomorphic to it, such a simplex.
Though technically not a fixed point theorem, the following result is closely related to the last theorem.
Theorem (Borsuk-Ulam Theorem). Every map $f:{\bf S}^n \to {\bf R}^n$ from an $n$-sphere to $n$-dimensional Euclidean space maps some pair of antipodal points to the same point: $$f(x)=f(-x).$$
A common interpretation of the case $n=1$ is that at any moment there is always a pair of antipodal points on the Earth's surface with exactly equal temperatures, or with equal barometric pressures.
Furthermore, an interpretation for $n=2$ is that there is always a pair of antipodal points with exactly equal temperatures and equal barometric pressures, simultaneously.
Exercise. Explain how the theorem implies that at any moment there is always a pair of antipodal points on the Earth's surface with identical wind.
Exercise. Derive the case $n=1$ of the theorem from the Intermediate Value Theorem.
Exercise. Prove the theorem. Hint: consider this map: $$g(x)=\frac{f(x)-f(-x)}{||f(x)-f(-x)||}.$$
An equilibrium of a market economy
Suppose we have a map $F:S \to S$. Applied consecutively, it creates a discrete dynamical system: $$X_{k+1}=F(X_k),$$ where $X_k \in S$ is the current state, at time $k$, of the system if it started at time $k=0$ at the state $X_0\in S$. Then the meaning of the equilibrium of the system is simple: $F(a)=a$. It's a fixed point!
A typical interpretation of such a system is a particle moving through a stream. We will consider instead the dynamics of prices in a simple market economy. Is it possible for them to stay constant? In other words, does every price dynamics allow an equilibrium?
Recall that we have $n$ commodities freely traded with possible prices that form a price vector $p=(p_1,...,p_n),$ at each moment of time. Then all positive, or even non-negative, prices are considered possible, i.e., the set of prices is $$P:={\bf R}_+^{n}.$$ The dynamics of prices is captured by a continuous function $F:P\to P$. However, we know that this isn't enough to conclude that there is a fixed point since $P$ isn't compact!
Let's make some additional assumptions in order to be able to guarantee an equilibrium.
How can we make the set of prices compact? One approach is to normalize the prices: $$p\mapsto \frac{p}{||p||},$$ under some norm so that the new prices form the $n$-simplex $\sigma$.
Exercise. Show that this is an equivalence relation. What assumption would guarantee that the price function is well-defined?
A more natural (if not more realistic) assumption is that the money supply is fixed. Suppose there are $n$ commodities. We assume that this is a pure exchange economy, i.e., there is no production of goods (other than making up for possible consumption). Then, there is only a fixed amount of each of the commodities: $$\bar{c}:=\sum_i c^i \in {\bf R}_+^n.$$ Then, the total cost of all the commodities, i.e., the total wealth $W>0$, is fixed too, for any combination of prices $p$: $$\langle p,c \rangle=W.$$ Then the space of prices can be set to be $$P:=\{p\in {\bf R}_+^{n}:\langle p, c \rangle =W\}.$$
Proposition. The set $P$ of prices with a fixed money supply is a convex polyhedron.
Exercise. Prove the proposition. What kind of polyhedron is it?
Therefore, the price map $F:P\to P$ has a fixed point by the Brouwer theorem.
Proposition. With a fixed money and commodity supply, a continuous price dynamics of an exchange economy has an equilibrium.
We have proven the existence of an equilibrium: there is such a combination of prices that, once acquired, will remain unchanged and all trading will happen in perfect harmony, forever... In reality, the outside events will be changing the function $D$ itself.
Exercise. What difference would price controls have?
Of course, this simple topological analysis won't tell us what this special combination of prices is, or how many of these are possible, or whether one of them will be reached (or even approached) from the current state.
Next, we consider the trading dynamics in this model. There are $m$ “agents” in the market and $i$th agent owns $c_j^i$ of $j$th commodity. These amounts form the $i$th commodity vector $c^i \in {\bf R}_+^n.$ The dynamics of distribution of commodities is captured by a continuous function $G:C\to C,$ where $$C:=\{(c^1,...,c^m):\ c^i\in {\bf R}_+^n\} = \left( {\bf R}_+^n \right)^m.$$ Once again, we know that this isn't enough to conclude that there is a fixed point since $C$ isn't compact!
We have to assume again that there is no production or consumption. Then, we can set instead: $$C:=\{(c^1,...,c^m):\ c^i\in {\bf R}_+^n,\ \sum_i c^i=\bar{c} \}.$$
Proposition. The set $C$ of commodities with a fixed commodity supply is a convex polyhedron.
Exercise. Prove the proposition. What kind of polyhedron is it?
Exercise. What if one is allowed to borrow?
Once again, there is a fixed point by the Brouwer theorem.
Proposition. With a fixed commodity supply, a continuous commodity dynamics of an exchange economy has an equilibrium.
In other words, there might be no trading at all!
We can combine these variables by defining the state of the system to be a combination of the prices and a distribution of the commodities. Then the state space is $$S:=P\times C,$$ and the state dynamics is given by a continuous function $D:S\to S$. Therefore, $S=P\times C$ is also a convex polyhedron and the map $D:S\to S$ has a fixed point by the Brouwer theorem.
How can we incorporate other quantities into this model? Any new quantity can be added to this model by simply extending the state space $S$ via the product construction. And there still be an equilibrium as long as:
- the next value of this quantity is determined by the circumstances not time,
- this dependence is continuous, and
- the range of its values is a priori bounded.
Exercise. What happens if we add interest rates to this model?
Chain maps of self-maps
We are to study fixed points of a map $f:|K|\to |K|$ by considering its homology map $f_*:H(K)\to H(K)$. However, the latter is built from the former via a simplicial approximation $g:K'\to K$, where $K'$ is an appropriate subdivision of $K$. However, $g$ cannot possibly be a self-map!
The invariance of homology can be restated as follows.
Proposition. Suppose $K'$ is a subdivision of a simplicial complex $K$, then $H(K') \cong H(K)$.
Then, two cycles are homologous in $K'$ if and only if their “counterparts” in $K$ are also homologous. What is the correspondence between the finer cycles in $K'$ and the coarser cycles in $K$?
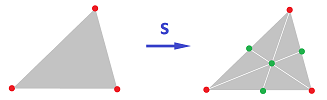
It is easy to find the counterpart in $K^m$ of a chain in $K$. We define the subdivision map $$s:K\to K'$$ on each $k$-simplex $x$ in $K$ by $$s(x):=\sum_ix_i,$$ with $x$ subdivided into the collection of $k$-simplices $\{x_i\}\subset K'$ oriented compatibly with each other and $x$.
Proposition. The subdivision map extended linearly to chains, $$s:C(K)\to C(K'),$$ is a chain map.
Exercise. Prove the proposition.
What about the opposite direction?
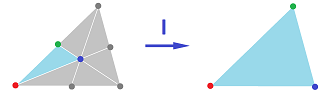
A simplicial approximation of the identity can be constructed as follows. Suppose, initially, that $K$ is an $n$-simplex and $K'$ is its barycentric subdivision. We define $I:K'\to K$ by first assigning to a vertex in $K'$ a vertex in $K$ following the rule: if vertex $A$ in $K'$ is the barycenter of simplex $A_0...A_m$ in $K$, we let $I(A)$ to be one of these vertices.
Proposition. There is exactly one $n$-simplex of $K'$ that is cloned (to the whole $K$) by $I$.
Proof. Suppose $C\in K'$ is the barycenter of the $n$-simplex $K$ and $I(C)=B\in K$. Then there is a face $\tau = B_0...B_{n-1}$ of $K$ the vertices of which are taken by $I$ to other vertices: $I(B_i)\ne B$. Next, let $C$ be the barycenter of the face $\tau$ and repeat the process. $\blacksquare$
Exercise. (a) Prove the uniqueness. (b) Show how the construction and the proof applies to the general case of a simplicial complex $K$ and its subdivision $K'=K^p$.
Theorem. The subdivision map generates the identity map on homology, $$s_*=\operatorname{Id}:H(K)\to H(K').$$
Proof. From the last proposition it follows that $I_{\Delta}s=\operatorname{Id}:C(K)\to C(K)$. $\blacksquare$
Thus, every self-map $f:|K|\to |K|$ does indeed have a matching chain self-map $sf:C(K')\to C(K')$ in the sense that $f_*=s_*f_*:H(K)\to H(K)$.
The Lefschetz number
The analogue of a fixed point free map is a cell map that is fixed cell free. It is a self-map $g:K \to K$ of a cell complex $K$ with $$g(s)\ne s, \ \forall s\in K.$$ What does it mean algebraically? Let's consider the chain maps of $g$, $$g_k:C_k(K)\to C_k(K), \ k=0,1,2,....$$ Then the above condition simply means that the diagonal elements of the matrix $A$ of $g_k$ are all zero! It follows, in particular, that the trace of this matrix, i.e., the sum of its diagonal elements: $$\operatorname{Tr}(A):=\sum_{i}A_{ii},$$ is also zero. We develop this idea further and convert it fully from the chain level to the homology level by means of a generalization of the Euler-Poincare formula.
Definition. The Lefschetz number of a self-map $f:S \to S$ of polyhedron $S$ is the alternating sum of the traces of the homology maps $[f_k]:H_{k}(S) \to H_{k}(S)$ of $f$: $$\Lambda (f):=\sum_{k}(-1)^{k}\operatorname{Tr}([f_k]).$$
With the alternating sum over the dimensions of the space, the formula resembles the Euler characteristic. This is not a coincidence: the latter is equal to the Lefschetz number of the identity function of $S$: $$\chi (S) = \Lambda (\operatorname{Id}_S).$$ This fact follows from the simple observation: $$\operatorname{Tr} (\operatorname{Id}:{\bf R}^n \to {\bf R}^n) = n.$$
Exercise. (a) Compute the Lefschetz numbers of $\delta P$ and $P \delta$, where $P:{\bf S}^2\to {\bf S}^2$ is the projection and $\delta:{\bf S}^2 \to {\bf S}^2 \times {\bf S}^2$ is the diagonal map. (b) Replace ${\bf S}^2$ with $M$, a path-connected compact surface.
The main result is below.
Theorem (Lefschetz Fixed Point Theorem). If a map $f:S \to S$ of a polyhedron $S$ has non-zero Lefschetz number, $$\Lambda (f) \ne 0,$$ then $f$ has a fixed point, $f(a)=a$, and so does any map homotopic to $f$.
If the polyhedron $S$ happens to be acyclic, we have $$[f_0]=\operatorname{Id}, \ [f_1]=0,\ [f_2]=0,\ ...,$$ and, therefore, $\Lambda (f) =1\ne 0$. The Brouwer Fixed Point Theorem follows.
Corollary. Suppose $S$ is a polyhedron with $\chi (S)\ne 0$ (such as a sphere) and a map $f:S \to S$ is homotopic to the identity, $f\simeq \operatorname{Id}_S$. Then $f$ has a fixed point.
The Lefschetz number only tells us that the set of fixed points is non-empty. The converse of course isn't true.
Example. Let $f$ be the flip of the figure eight, ${\bf S}^1 \vee {\bf S}^1$, one loop onto the other. Then $$[f_0]=1,\ [f_1]=\left[ \begin{array}{cc} 0 & 1\\ 1 & 0 \end{array} \right],\ [f_2]=0,...$$ Therefore, $$\Lambda (f) =1-0=1.$$ Not only there is a fixed point, as we can see, but also any map homotopic to $f$ has a fixed point.
$\square$
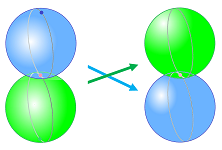
Example. We consider the flip of the “kissing spheres” space, ${\bf S}^2 \vee {\bf S}^2$, one sphere onto the other:
Then $$[f_0]=1,\ [f_1]=0,\ [f_2]=\left[ \begin{array}{cc} 0 & 1\\ 1 & 0 \end{array} \right],\ [f_3]=0,....$$ Therefore, $$\Lambda (f) =1-0+0=1.$$
$\square$
Exercise. Consider the flip of the “double banana”.
Exercise. Consider the other flip of the figure eight, the “kissing spheres”, and the “double banana”.
Exercise. Suggest a map with $\Lambda (f) \ne 0$ but $\Lambda (f)=0$ modulo $2$.
The beginning of the proof of the Lefschetz theorem is similar to that of the Euler-Poincare formula, except, we will manipulate the traces of linear operators rather than the dimensions of subspaces (after all $\dim V=\operatorname{Tr}(\operatorname{Id}_V)$). We rely on the following fact from linear algebra.
Lemma. Suppose we have a commutative diagram with exact rows: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} 0 & \to & U & \hookrightarrow & V & \to & W & \to & 0 \\ & & \da{f^U} & & \da{f} & & \da{f^W} \\ 0 & \to & U & \hookrightarrow & V & \to & W & \to & 0. \end{array} $$ Then, $$\operatorname{Tr} (f) = \operatorname{Tr} (f^U) + \operatorname{Tr} (f^W).$$
Exercise. Prove the lemma.
Exercise. Show that the lemma implies the proposition in subsection 1.
Next, we apply this lemma, for each $k=0,1,2,...$, to
- the chain map $f_k:C_k \to C_k$,
- its restriction $f^Z_k$ to the subspace of cycles $Z_k$,
- its restriction $f^B_k$ to the subspace of boundaries $B_k$, and
- the homology map $[f_k]$ induced by $f$.
Exercise. Apply the lemma to $$U=Z_k \hookrightarrow V=C_k \xrightarrow{\quad \partial_k \quad} W=B_{k-1}.$$
Exercise. Apply the lemma to $$U=B_k \hookrightarrow V=Z_k \xrightarrow{\quad q \quad} W=H_k,$$ where $q$ is the quotient map.
The conclusions are: $$\operatorname{Tr} (f_k) = \operatorname{Tr} (f^Z_k) + \operatorname{Tr} (f^B_{k-1}),$$ $$\operatorname{Tr} (f_k^Z) = \operatorname{Tr} ([f_k]) + \operatorname{Tr} (f^B_{k}).$$ Next, we use these two identities to simplify the following alternating sum: $$\sum_k (-1)^k \left( \operatorname{Tr} (f_k) - \operatorname{Tr} (f_{k-1}^B) \right)=\sum_k (-1)^k \left( \operatorname{Tr} ([f_k]) + \operatorname{Tr} (f^B_{k}) \right).$$ The terms with $f^B$ in the left-hand side and the right-hand side cancel. The result is this generalization of the Euler-Poincare formula.
Theorem (Hopf Trace Formula). $$\sum_k (-1)^k \operatorname{Tr} (f_k) =\sum_k (-1)^k \operatorname{Tr} ([f_k]).$$
The result is purely algebraic. In fact, similar to the Euler-Poincare formula, the algebra of the formula is identical on the left and right but applied to two different sequences of linear operators. This observation justifies the definition of the Lefschetz number of an arbitrary sequence of linear (self-)operators $h=\{h_k:\ k=0,1,2...\}$, as follows: $$L(h):=\sum_k (-1)^k \operatorname{Tr} (h_k).$$ Then the trace formula becomes: $$L(h)=L([h]).$$ At this point, the latter is recognized as $\Lambda (f)$ if we choose $h=f_{\Delta}$.
Exercise. Show that $L$ is a linear operator.
Now we finish the proof of the fixed point theorem.
Suppose map $f:S\to S$ has no fixed points. Since $S$ is compact, there is an $\epsilon >0$ such that $$d(x,f(x))>\epsilon$$ for all $x\in S$. Suppose $S=|K|$ for some simplicial complex $K$. We subdivide $K$ enough times, $p$, so that $\operatorname{mesh}^*(K^p)<\epsilon $. Then $$d(\sigma,f(\sigma))>\operatorname{mesh}^*(K^p)$$ for all $\sigma \in K^p$.
We rename $K^p$ as $K$ and proceed to the next step. According to the Simplicial Approximation Theorem, we can acquire a simplicial approximation $g:K^m\to K$ of $f$: $$f(N_A)\subset N_{g(A)}$$ for any vertex $A$. We do so for finer and finer subdivisions of $K$ -- until we have $$\sigma \cap g(\sigma)=\emptyset$$ for all $\sigma \in K^m$. It follows that $$sg_{\Delta}(\sigma)\ne\sigma,$$ where $s$ is the subdivision chain map from the last subsection. Then, $$L(sg_{\Delta}):=\sum_k (-1)^k \operatorname{Tr} (s_kg_k) = \sum_k (-1)^k 0 = 0.$$ By the Hopf Trace Formula, we have $$\Lambda (f) :=\Lambda (g_*) =L (sg_{\Delta}) =0.$$
This finishes the proof of the Lefschetz theorem.
Exercise. Prove that $\Lambda (hfh^{-1}) = \Lambda (f)$ for any homeomorphism $h$.
The degree of a map
The degree is initially introduced for maps of the circle: $$f:{\bf S}^1 \to {\bf S}^1,$$ as the number of times the first circle wraps around the second.
The degree is also defined for maps $$f:{\bf S}^1 \to {\bf R}^2 \setminus \{0\},$$ as the “winding number”. It is computed by using a polar coordinate parametrization, then measuring the change in the angle, and setting $$\deg f:=\frac{\theta (1) -\theta (0)}{2\pi}.$$
We, instead, approach the idea homologically.
Let's consider the homology map induced by our map: $$[f_1]: {H}_1({\bf S}^1) \to {H}_1({\bf S}^1). $$ Since both of the groups are isomorphic to ${\bf Z}$, group theory tells us that such a homomorphism must be the multiplication by an integer. This integer is the degree of $f$.
The idea and the construction are now applied to a more general case.
Definition. Given a map between any two $n$-dimensional compact, path-connected manifolds $$f:M^n \to N^n,$$ the degree $\deg f$ of $f$ is the integer that satisfies: $$[f_n](x)=\deg f \cdot x,$$ where $$[f_n]: H_n(M^n) \cong {\bf Z} \to H_n(N^n)\cong {\bf Z}. $$ is the homology map of $f$.
Exercise. Prove the following.
- 1. The degree of the constant map is $0$.
- 2. The degree of the identity map is $1$.
- 3. The degree antipodal map of the $n$-sphere ${\bf S}^n \subset {\bf R}^{n+1}$ is $(-1)^{n+1}$.
We will accept the following without proof (Bredon, p. 187).
Theorem. The degree of a reflection of the $n$-sphere ${\bf S}^n \subset {\bf R}^{n+1}$ through an $(n+1)$-dimensional hyperplane containing $0$, such as $$f(x_1,x_2,...,x_n,x_{n+1})=(-x_1,x_2,...,x_n,x_{n+1}),$$ is $-1$.
Exercise. Any map $f: {\bf S}^n \to {\bf S}^n$ can be used as an attaching map of a cell complex. Suppose two such maps $f,g$ of degrees $k,m$ are used to attach two copies of ${\bf B}^{n+1}$ to ${\bf S}^n$. Compute the homology of the resulting cell complex for all $k,m$. Hint: start with $n=1,k=1,m=2$.
The following theorems are derived from the properties of homology maps.
Theorem. The degree is multiplicative under compositions, i.e., $$\deg(fg) = \deg(f)\cdot\deg(g).$$
Theorem. The degree is homotopy invariant, i.e., $$f\simeq g \Longrightarrow \deg(f) = \deg(g).$$
Theorem. The degree of a homeomorphism, or even a homotopy equivalence, is $\pm 1$.
Exercise. Prove the theorems.
The following is an easy computation.
Theorem. For a map $f: {\bf S}^n \to {\bf S}^n$ of spheres, we have $$\Lambda (f) = 1 + (-1)^{n+1}\deg f.$$
Corollary. A map $f: {\bf S}^n \to {\bf S}^n$ with $\deg f \ne (-1)^n$ has a fixed point.
It follows that a map of spheres not homotopic to a homeomorphism will have a fixed point.
The theorem below provides a partial solution of the problem of surjectivity.
Theorem. A map $f: {\bf S}^n \to {\bf S}^n$ of nonzero degree is onto.
Proof. If $a\in {\bf S}^n \setminus \operatorname{Im} f $, the image is contractible as a subset of a contractible set ${\bf S}^n \setminus \{a\}$, the latter fact proven via the stereographic projection. Therefore, $f$ is homotopic to the constant map and $\deg f =0$, a contradiction. $\blacksquare$
Notice that ${\bf T}^2 \setminus \{a\}$ isn't contractible and that's why the proof fails if applied to an arbitrary pair of manifolds. A more general result will be provided later.
Exercise. Provide details of the proof and then make both the proof and the statement of the theorem as general as possible.
Exercise. What is the converse of the theorem? Hint: don't try to prove it.
Let's recall also the argument we made about the solvability of the Extension Problem for maps of spheres.
Theorem. A map $f: {\bf S}^n =\partial {\bf B}^{n+1} \to {\bf S}^n$ of $n$-spheres of non-zero degree cannot be extended to a map on the whole ball, $F: {\bf B}^{n+1} \to {\bf S}^n$.
Proof. The fact follows from the commutativity of the following diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccc} &{\bf S}^n & \hookrightarrow &\ {\bf B}^{n+1} \\ & & _{f} \searrow & \ \da{F=?} \\ & & & {\bf S}^n \end{array} $$ $\blacksquare$
Exercise. Provide details of the proof and then make both the proof and the statement of the theorem as general as possible.
Zeros of vector fields
First, we will see what the Brouwer Fixed Point Theorem tells us about zeros of vector fields.
Suppose a vector field $V$ is defined on a subset $R\subset {\bf R}^n$ which is homeomorphic to ${\bf B}^m, \ m<n$. We know that $V$ determines a map $f$ but is it a self-map? If it is, the map will have a fixed point.
We know that we can just follow the direction of $V(x)$ to define $f(x)$ but how far? We will say that $V$ points inside $R$ if for every $x\in \partial R$ there is $\epsilon >0$ such that $\epsilon V(x) \in R$.
Exercise. Prove that, in that case, there is $\epsilon >0$ such that $\epsilon V(x) \in R$ for all $x\in R$.
Then $f(x):=\epsilon _x V(x)$ is well defined as a map $f:R\to R$. Therefore $f$ has a fixed point, $V$ has a zero, and, if $V$ defines an ODE, there is a stationary point.
We can do more with the Lefschetz Fixed Point Theorem, without requiring that $V$ points inside $R$.
We know that, if the forward propagation map $Q_t:R \to S$ of $V$ is well-defined for some $S\subset {\bf R}^n$, and some $t>0$, and $R$ is a deformation retract of $S$, then we have: $$rQ_t \simeq \operatorname{Id}_R,$$ where $r:S\to R$ is the retraction. We also know that $$\Lambda (rQ_t) = \Lambda (\operatorname{Id}_R) = \chi (R).$$ Therefore, when $\chi (R) \ne 0$, map $rQ_t$ has a fixed point by the corollary to the Lefschetz Fixed Point Theorem. Whether this means that $V$ has a zero depends on $r$.
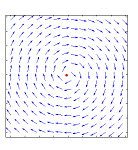
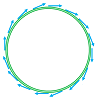
It is easy to design a non-zero vector field for a circle. In fact, we can have a unit vector field:
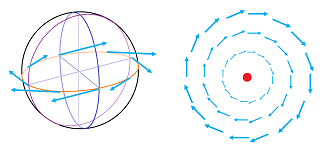
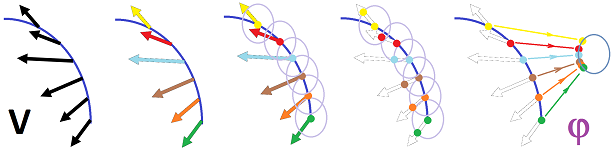
We run into problems if try this idea for a sphere. If we are to assign vectors of equal length to points of equal latitude, we realize that their lengths would have to diminish as we approach the pole to assure continuity:
Theorem (Hairy Ball Theorem). A continuous vector field tangent to the even-dimensional sphere has a zero.
For dimension $2$, it reads: “you can't comb the hair on a coconut”.
Exercise. What about the torus?
Exercise. Prove the theorem.
Example (cyclone). Another commonly known interpretation of the theorem is the following. The atmosphere forms a layer around the Earth and the air moves within this layer.
Assuming that this layer is “thin”, what we have is a sphere. Therefore, the vector field of the wind has a stationary point, which is a point where the wind speed is $0$. That point might be a cyclone.
$\square$
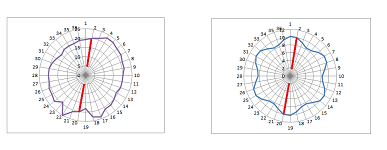
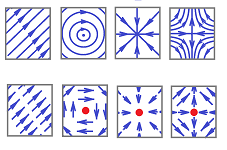
What if next we want to be able to distinguish the following behaviors of vector fields:
We can consider only the behavior of the vector field $V$ on the boundary of the neighborhood. In the $2$-dimensional case, we can simply evaluate the rotation of $V$ along this curve. It is $0$ for the first one and $2\pi$ for the rest of them. This approach to detecting zeros applies to every vector field with no zeros on the boundary. Problem solved!
What about higher dimensions? The boundary of an $n$-ball is an $(n-1)$-sphere, not a curve. What is the analog of the rotation then?
A convenient way to compute the rotation of a vector field $V:{\bf B}^2 \to {\bf R}^2$ with $V(u) \ne 0, \ \forall u\in \partial {\bf B}^2$, is to normalize it first: $$\phi(u):=\frac{V(u)}{||V(u)||}.$$ The result is a new function, $\phi :{\bf S}^{1} \to {\bf S}^{1}$:
Then the rotation of $V$ along the boundary of the disk is simply $2\pi\cdot\deg \phi $!
Suppose $D$ is a closed ball neighborhood in ${\bf R}^n$ and vector field $V$ has no zeros on its boundary $\partial D$.
Definition. We define the Gauss map of $V$ on $D$, $$\phi_D:\partial D \to {\bf S}^{n-1},$$ by $$\phi_D(z):=\frac{V(z)}{||V(z)||}.$$
Now, if $V$ has no zeros on the whole $D$, the Gauss map can be extended to the whole $D$ with the same formula. But by the last theorem from the last subsection, such an extension is only possible if $\deg \phi _D =0$.
Definition. We define the index of a vector field $V$ on $D$, $\operatorname{Index}_D (V)$, to be the degree of the Gauss map: $$\operatorname{Index}_D (V):=\deg \phi _D.$$
Exercise. Prove that the index is independent from the choice of $D$.
We have the following.
Theorem. If $\operatorname{Index}_D (V)\ne 0$ then vector field $V$ has a zero in $D$.
The following is a generalization (it follows from the Lefschetz Fixed Point Theorem) we will state without proof (see Bredon).
Theorem (Poincaré–Hopf Index Theorem). Suppose a continuous vector field $V$ has only isolated zeroes in domain $Q\subset {\bf R}^n$ and suppose that $V$ points in the outward normal direction along the boundary of $Q$. Then we have the formula: $$\sum_i \operatorname{Index}_{D_i}(V) = \chi(Q),$$ where the sum is over neighborhoods of all the zeroes of $V$.
Therefore, if $\chi (S)\ne 0$, there is a zero just as in the previous theorem.
Social choice: gaming the system
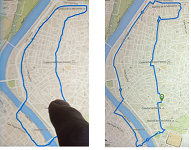
Let's recall the two hikers that are about to go into the woods and they need to choose (or we may suggest to them) a procedure on how to decide where to set up their camp, as a fair compromise.
This procedure should be equally applicable to the future in case they decide to take a trip again. The answer is simple: take the middle point between the two locations, if possible. It is always possible when the forest is convex.
Now, what if one of the participants decides to manipulate the situation and, while his (true but possibly secret) preference point remains the same, declares his choice to be a point farther away from the other person's choice?
Then the mid-point, compromise point moves closer to the first person's preferred location!
Seeing this, the other person would move his declared choice in the opposite direction as well. They respond to to each other in this fashion and this turns into a hostile game!
Example. To be able to fully analyze such a game, let's consider its simpler, $1$-dimensional version: the choices are limited to a straight segment of a road in the forest. Suppose the players counteract each other's moves by moving backwards continuously. In that case, this game will go on until one of them reaches the end of the road (i.e., the edge of the forest). Then the other person continues to gain ground until the “compromise” location coincides with his or otherwise until he also reaches the end of the road.
The three possible outcomes share an interesting property: neither player can improve his position by a unilateral action! Such a state is called a Nash equilibrium.
Let's confirm this analysis with a quick computation.
Suppose the road is the interval $[0,1]$ and the preferred locations of the two players are $A_1$ and $A_2$ respectively. We assume that $A_1<A_2$ and they remain unchanged. However, the players choose points $x_1$ and $x_2$. Either makes his selection as he tries to decrease the distance from the preferred location to the compromise, midpoint location. In other words, $i$th goal is to
- minimize the harm $h_i:=|A_i-\frac{1}{2}(x_1+x_2)|$,
or to maximize some related utility. We have: $$0 \le x_1 \le A_1 < A_2 \le x_2 \le 0.$$ If $x_1$ is chosen and fixed, the response of the second player would be to try to get the prefect hit and choose $x_2$ so that $$\frac{1}{2}(x_1+x_2)=A_2,$$ if possible. Then $$x_2=r_2(x_1):=\min\{1,\ 2A_2-x_1\}.$$ Similarly, if $x_2$ is chosen and fixed, the response of the first player is $$x_1=r_1(x_2):=\max\{0,\ 2A_1-x_2\}.$$ These maps are continuous!
To have an equilibrium, we need $x_1=r_1(x_2)$ and $x_2=r_2(x_1)$. However, we can't have both $x_1$ and $x_2$ within $(0,1)$; otherwise, $$x_1=2A_1-x_2, \ x_2=2A_2-x_1,$$ which leads to a contradiction: $A_1=A_2$. Let's assume that $x_1=0$. Then $x_2=2A_2$ or $1$, just as depicted.
$\square$
We summarize this analysis with the following.
Definition. For a pair of maps $$r_1:X_2\to X_1,\ r_2:X_1\to X_2,$$ its Nash equilibrium is a fixed point of $R:X_1\times X_2 \to X_1\times X_2$, where $$R(x_1,x_2):=(r_1(x_2),r_2(x_1))$$ is a function that may be called the combined response function.
This function can also be defined to be: $$R:=\tau (r_2\times r_1),$$ where $\tau :X_1\times X_2 \to X_2\times X_1$ is the transposition: $\tau(x_1,x_2)=(x_2,x_1)$.
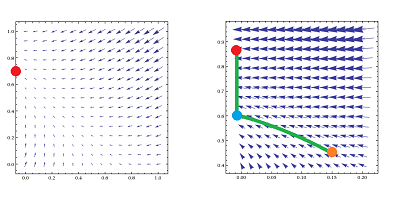
This function can be illustrated as a vector field. In particular, for the example above with $A_1=.15,A_2=.45$, the vector field looks like this:
The path taken by the pair of players is also shown.
The Brouwer Fixed Point Theorem implies the following.
Theorem. Suppose $X$ is an acyclic polyhedron, then any pair of self-maps of $X$ allows a Nash equilibrium.
The key to this theorem is not only the acyclicity of the space of choices but also the continuity of the response map. The continuity assumption is natural but the uniqueness of a possible response is not. For example, when the above game is played not on a segment of a road but in a forest, the response isn't unique (one can more deviate from the straight line) and the simple theorem above won't apply.
Exercise. Prove that the response is unique in the case of a convex forest.
Let's follow the example and assume that either player wants to maximize some utility of his own: $$u_1:X\times X\to {\bf R},\ u_2:X\times X\to {\bf R}.$$ Then, in general, the maxima of these functions are attained for multiple values of $x$.
One way to avoid having to deal with set-valued maps is thinking of this game as a dynamical system, as follows. Suppose $X$ is a closed domain in ${\bf R}^n$ and the utilities $u_1,u_2$ are defined on some open neighborhood of $X$. Then to find a maximum, all we need to do is to follow the gradients. The gradients of the utilities define a vector field $V$ (just as illustrated above): $$V_x=\operatorname{grad}_x u_1(x,y),\ V_y=\operatorname{grad}_y u_2(x,y). $$ Then the Poincaré–Hopf Index Theorem applied to $V$ implies the following.
Theorem. Suppose the utilities are continuously differentiable on an open neighborhood of a domain $Q\subset {\bf R}^n$ and suppose that their gradients point in the outward normal direction along the boundary of $Q$. Then, provided $\chi(Q) \ne 0$, the utilities have critical points in $Q$.
If the utilities are also concave down, these points are the maxima. We have an analogue of a Nash equilibrium.
Exercise. Without the convexity condition, what can we say about how the game is played around these points?