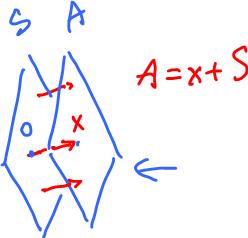This site is being phased out.
Linear algebra
Contents
Linear subspaces of R3
Any subset $U$ of ${\bf R}^3$ that is closed with respect to the operations of ${\bf R}^3$ is called linear subspace or simply subspace.
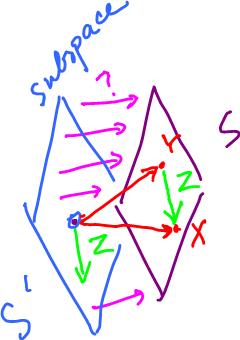
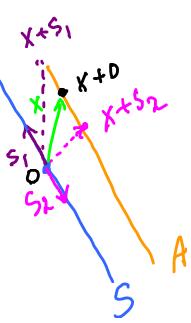
Example. Suppose u = (0,1,1). Is there a y such that y ∈ S\S1, where S = Span{u}?
Yes, for example v = (1,1,2).
Next compute
S2 = Span(u, v)
= {αu + βv: α, β ∈ R}
= {α(0,1,1) + β(1,1,2): α, β ∈ R}
= {(β,α+β,α+2β): α, β ∈ R}
The result is the "parametric solution" of the system. It is plane in the 3-space.
Theorem 1.4.3 The solution set of a homogeneous linear equation
a1x1 + a2x2 + a3x3 = 0,
with at least one of a1, a2, a3 not equal to 0, is a plane passing through the origin.
If a1 = a2 = a3 = 0, the the equation turn into 0 = 0, and the solution set is R3.
Example. Given:
u = (1,1,0), v = (1,0,1), w = (3,1,2).
Do they all lie in a 2-dimensional subspace?
Find if w ∈ Span{u, v}? In other words.
w = αu + βv.
Find α, β.
Rewrite the equation:
(3,1,2) = α(1,1,0) + β(1,0,1) (3,1,2) = (α+β, α, β)
Examining each coordinate of this vector equation produces three equations for these numbers:
3 = α + β ______ (1) 1 = α + 0 ______ (2) 2 = 0 + β ______ (3)
Solve it.
There are 2 unknowns but 3 equations. So the solution of any two equations must satisfy the third. From (2) and (3) we have α = 1 and β = 2 which when substituted in (1), we see that (1) is satisfied.
Hence, the solution is w = u + 2v. In other words, u = w - 2v and v = (w - u)/2. The solution set is the plane is x + 2y - z = 0.
Example. Given
x1 = (1,2,3)
x2 = (1,2,-3) [it follows that x2 ∉ Span{x1}]
x3 = (1,4,0).
Find Span{x1, x2, x3}.
Denote
| 1 2 3| | 1 2 -3| = [A], say. | 1 4 0|
Then
det(A) = 0 - 6 + 12 - 6 + 12 - 0 = 12
Since the determinant is non-zero so the vectors are linearly independent, hence
Span{x1, x2, x3} = R3.
Example. Represent the solutions of the (system) equation:
x3 = 0
as linear combinations of two fixed vectors.
Consider the solution set of an equation:
S = {x3 = 0}
= {(*, *, 0)}
= {(α, β, 0): α, β ∈ R}
= {α(1,0,0), β(0,1,0): α, β ∈ R}.
Moreover,
(1,0,0) = e1, (0,1,0) = e2 form a basis of S.
Example. Same problem for:
x1 - x2 + x3 = 0
Let's guess first:
u = (1, 1, 0), v = (0, 1, 1).
Check
u = λv? (1, 1, 0) = λ(0, 1, 1) (1, 1, 0) = (0, λ, λ)
Clearly there is no solution for non-zero λ.
Without a guess:
x1 = 0 implies -x2 + x3 = 0, so x2 = x3
Pick
x3 = 1 then u = (0, 1, 1).
Single linear equation
Let's start with these examples:
Homogeneous equation: x1 + x2 - x3 = 0 Non-homogeneous equation: x1 + x2 - x3 = 1 [The right hand side is any non-zero number]
The solution set S of the second equation is not a subspace.
Indeed, let us assume that the set S be a linear subspace. Let
x = (1,0,0) and y = (3,0,2) be two vectors in S.
For S to be a linear subspace the linear combination of u and v must also be vector in S. Let
z = x + y = (1+3, 0+0, 0+2) = (4,0,2).
Now, take the coordinates of w and substitute them into the equation:
z1 + z2 - z3 = 4 + 0 - 2 = 2 ≠ 1.
Therefore w ∉ S and so
S is not a linear subspace.
But what about
z = x - y? z = (1-3, 0-0, 0-2) = (-2, 0, -2).
So, z1 + z2 - z3 = -2 + 0 + 2 = 0 ≠ 1. So, in this case too z ∉ S.
But, z = x - y satisfies the homogeneous equation!
This is also true in general case:
if x, y ∈ S = {x1 + x2 - x3 = 1}
then x - y ∈ S' = {x1 + x2 - x3 = 0}.
Indeed, let x and y be
x = (x1, x2, x3) ∈ S and y = (y1, y2, y3) ∈ S.
Then,
z = x - y = (x1 -y1, x2 -y2, x3 -y3) ∈ S
Now, since u,v ∈ S so
x1 + x2 - x3 = 0 y1 + y2 - y3 = 0 _____________________________ (x1 -y1) + (x2 - y2) - (x3 - y3) = 0
Therefore, z ∈ S'.
The S and S' are two parallel planes:
S: x1 + x2 - x3 = 1, S': x1 + x2 - x3 = 0.
This means that S' is obtained from S by a shift. Find it.
Theorem. Given a non-homogeneous linear equation, its solution set has the form
S = S1 + z,
where S1 is the solution set to the corresponding homogeneous equation (subspace) and z is a vector.
Example. Consider an equation (solution set S is a plane):
2x1 - x2 + 3x3 = 5.
Rewrite:
2x1 = x2 - 3x3 + 5, x1 = (1/2)x2 - (3/2)x3 + (5/2).
Let x2 = α and x3 = β be the parameters. Then,
x1 = (1/2)α - (3/2)β + (5/2).
A solution is x = (x1, x2, x3) ∈ R3, so
x = ((1/2)α - (3/2)β + (5/2), α, β) where α, β ∈ R
S is the set of all such x's. Thus,
x = αx1 + βx2 + z
Here:
z = (0, 0, 5/2), x1 = (1, 0, 1/2), x2 = (0, 1, -3/2).
This is the answer.
Two linear equations
Consider a system of two equations:
S1: x1 + x2 - x3 = 0 S2: x1 + 2x2 + x3 = 0
Here the solution to each equation is a subspace. Then, the solution set of the intersection of these two subspaces is their intersection:
S = S1 ∩ S2.
S may be a line...
Adding the two equations:
2x1 + 3x2 = 0, x1 = -(3/2)x2.
Substituting in the equation for S1:
-(3/2)x2 + x2 - x3 = 0 -(1/2)x2 - x3 = 0 x3 = -(1/2)x2
Choose a parameter
x2 = α.
Then, the solution set S is given by:
x1 = -(3/2)α x2 = α x3 = -(1/2)α
This solution
S = (-(3/2)α, α, -(1/2)α) represents a straight line in R3.
Also,
S = {αx: α ∈ R}, where x = (-3/2, 1, -1/2)
Now what if these equations had a non-zero entries in the right hand sides ("free terms")?
We rewrite the work above and change just a few things:
S*1: x1 + x2 - x3 = 1, S*2: x1 + 2x2 + x3 = 2.
The solution set S is the intersection of these two subspaces:
S* = S*1 ∩ S*2.
Adding the two equations:
2x1 + 3x2 = 3, x1 = -(3/2)x2 + (3/2)
Substituting in the equation for S*1:
-(3/2)x2 + (3/2) + x2 - x3 = 1, -(1/2)x2 - x3 = -(1/2), x3 = -(1/2)x2 + (1/2).
Suppose, x2 = α. Then, the solution set is
x1 = -(3/2)α + (3/2) x2 = α x3 = -(1/2)α + (1/2)
In other words,
S* = (-(3/2)α + (3/2), α, -(1/2)α + (1/2)) represents a straight line in R3.
Also,
S* = {αx: α ∈ R} + z where x = (-3/2, 1, -1/2) and
z = (3/2, 0, 1/2)
Hence, S* = S + z.
Example of two equations but solution set is a plane:
x1 + x2 + x3 = 0 2x1 + 2x2 + 2x3 = 0.
In this case the second equation is redundant (it's an identical plane).
Three linear equations
Solution for 3 equations can be
1) Point - when the equations represent planes with no parallel ones; 2) Plane - when the equations represent identical planes; 3) Line - when the equations represent planes that intersect through it; 4) R3 - when for example the equations are 0 = 0.
Example. Find the solution set of the system:
x1 - x3 = 3 _____ (1) x2 + 3x3 = 5 ______ (2) 2x1 - x2 - 5x3 = 1 ______ (3)
Substituting x1 from (1) into (3):
2(x3 + 3) - x2 - 5x3 = 1 x3 - 3x2 = -5 _____ (4)
Comparing (4) with (2) it is evident that (4) is a multiple of (2). Comparing (1) with (2) it is evident that (2) is not a multiple of (1). Then, the solution set is a line.
Specifically, we have 1 parameter, say, α = x3. Then the solution set is:
1) x1 = α + 3 2) x2 = -3α + 5 3) x3 = α
In other words,
x = (x1, x2, x3) = (α + 3, -3α + 5, α).
Next
S = span{x} + z,
find x and z:
x = (1, -3, 1) and z = (3, 5, 0).
Example. Find α1, α2, α3 so that
{Solution of α1x1 + α2x2 + α3x3 = 0} = Span{x1, x2}, where
x1 = (1, -1, 1) and x2 = (2, 1, 1).
Rewrite:
Span{x1, x2}
= {αx1 + βx2: α, β ∈ R}
= {(α + 2β, -α + β, α + β: α, β ∈ R}
Solution:
x1 = α + 2β x2 = -α + β x3 = α + β
Substitute:
α1(α + 2β) + α2(-α + β) + α3(α + β) = 0 α(α1 - α2 + α3) + β(2α1 + α2 + α3) = 0
Since α and β are arbitrary, we have
(α1 - α2 + α3) = 0 (2α1 + α2 + α3) = 0
Exercise: solve this system.
Review example. Given: u = (1,1,0), v = (0,1,1). Is vector (0,1,-1) a linear combination of u and v? In other words, find α and β such that
(0,1,-1) = αx1 + βx2
Rewrite:
(0,1,-1) = α(1,1,0) + β(0,1,1) = (α, α + β, β) 0 = α, 1 = α + β, -1 = β
This is clearly a contradiction.
More generally,
Theorem. A system of m homogeneous equations with n unknowns has infinitely many solutions when n > m.
Geometrically,
n = dimension of the space and m = no. of linear subspaces S1, S2, .... Sm corresponding to each equation.
The solution set of the system is the intersection of S1, S2, .... Sm:
S = S1 ∩ S2 ∩ .... ∩ Sm
Then S a linear subspace of Rn.
Observe that 0∈S. Now, if S ≠ 0, then there is x∈S \ {0}. Then there are more solutions:
span{x} ⊂ S.
Examples. (1) Solve the system:
x1 = 0, x3 = 0
Then
S = {(0, α, 0): α ∈ R}
= line = span{(0, 1, 0)}.
(2) Solve the system:
x1 - x3 = 0 x1 + x3 = 0 ____________ 2x1 = 0 x1 = 0
Substituting for x1 we get x3 = 0. The answer is the same as above.
(3) Solve the system:
x1 - x2 = 0 -x1 + x2 = 0.
Then
x1 = x2
Find
S = Span{v1, v2}.
Let x2 be a parameter α and x3 be a parameter β. Then
S = {(α, α, β): α, β ∈ R}
= {αv1 + βv2: α, β ∈ R}
= {α(1,1,0) + β(0,0,1): α, β ∈ R}
S = Span{(1,1,0), (0,0,1)}
Next,
line = intersection of planes P1 (equation 1) and P2 (equation 2).
Examples. Consider these systems:
(1)
x1 + x2 + x3 = 1 x1 + x2 + x3 = 2
(2)
x1 + x2 + x3 = 1 (same equation) 2x1 + 2x2 + x3 = 1
Subtracting:
-x1 + x2 = 0,
so there are infinitely many solutions.
(3)
x1 + x2 = 1 x1 + x2 = 1 x1 + x2 = 1
So there are infinitely many solutions.
(4)
0∙x1 + 0∙x2 + 0∙x3 = 1, then 0 = 1.
So there is no solution.
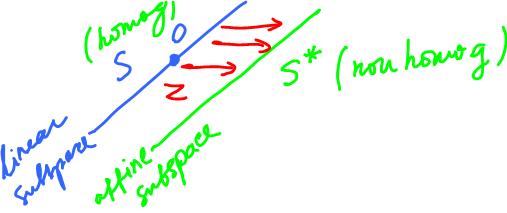
Affine subspaces
An affine subspace A is a subset given by
A = x + S,
where S is a linear subspace and x is a vector.
Here is what we mean here:
A = x + S = {x + s: s ∈ S}
set = vector + set.
Of course, this representation doesn't have to be unique:
A = x1 + S = x2 + S = x3 + S.
What do we know about x?
First,
O ∈S, so 0 + x ∈ A, or x ∈ A.
On the other hand,
if x' ∈ A then x' + S = A.
Suppose, A = x + S = y + T (equal as sets), where S, T are linear subspaces. Then, S = T and y ∈ A.
The converse is also true i.e.
if S = T and y ∈ A then A = y + T = x + S.
Affine subspaces are solution sets of systems of non-homogeneous equations.
Example. System of non-homogeneous equations:
x1 + x2 + x3 = 1 ________ (1) x1 - x3 = 2 ________ (2)
Transforming into the corresponding system of homogeneous equations:
x1 + x2 + x3 = 0 x1 - x3 = 0
The solution set to the latter is a linear subspace, say, S and the solution to the former is, say, A. Then
A = S + x.
What is x?
First, x is a solution to the non-homogeneous system:
x∈A.
Suppose we have S, find A. Turns out, all we need is x, i.e., any single solution to the non-homogeneous system.
If x = (3, -3, 1) then A = (3, -3, 1) + S. If x = (2, -1, 0) then A = (2, -1, 0) + S.
The values of x is such that substitution into equation (1) and (2) satisfies both.
Theorem. The solution set A of a non-homogeneous system of equations is the sum of the solution set S of the corresponding homogeneous system of equations and any solution x of the non-homogeneous system:
A = x + S.
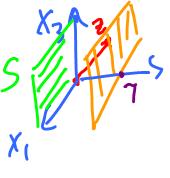
Case 1. Let us consider the case with 2 equations and 3 variables. The solution set corresponds to the intersection of 2 planes in R3. This is typically a line and atypically either no intersection (parallel planes) or coincident planes.
Case 2. Let us consider the case with 3 equations and 3 variables. The solution set corresponds to the intersection of 3 planes in R3. This is typically a point and atypically either no intersection (parallel planes) or a line.
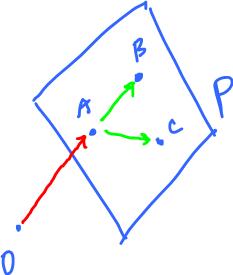
We know that a plane is determined by three points. Or we can use vectors instead:
P = x + S, where S = Span(v1, v2).
To find these vectors:
x = OA, v1 = AB, v2 = AC.
Review example. Find a1, a2, a3 so that
{Solution of a1x1 + a2x2 + a3x3} = 0} = Span{x1, x2},
where x1 = (1, -1, 1) and x2 = (2, 1, 1).
Substituting x1 and x2, separately, in the given equation we have
a1×1 + a2×(-1) + a3×1 = 0 _____ (1) a1×2 + a2×1 + a3×1 = 0 _____ (2)
Let' solve the system. Rearranging the equations (1) and (2),
a1 - a2 + a3 = 0 ______ (3) 2a1 + a2 + a3 = 0 ______ (4)
We have a system of 2 equations and 3 unknowns so we need 1 more equation to make the answer unique. Taking
a2 = 1,
we can rewrite equations (3) and (4) as
a1 + a3 = 1 _____ (5) 2a1 + a3 = -1 _____ (6)
Solving (5) and (6), we have
a1 = -2, a3 = 3.
To verify, back substituting a1, a2 and a3 into the original equation (3) we have
a1 - a2 + a3 = 0 -2 - 1 + 3 = 0
Therefore, the answer is (-2, 1, 3).
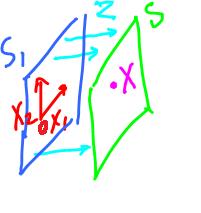
Review example. If
S1 = Span{x1, x2} and
S2 = Span{y1, y2}.
Find z such that P = S1 ∩ S2. To rephrase,
S1 ∩ S2 = Span{z}, so
z ∈ S1 ∩ S2, or
z ∈ S1 and z ∈ S2.
Rewriting the last part:
(z = ) αx1 + βx2 = γy1 + δy2.
Find α, β (γ, δ).
Dimension of vector space
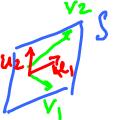
Consider a system of two equations:
x1 + x2 - x3 = 0 2x1 + 2x2 - 2x3 = 0
Then
S = Span{u1, u2}
= Span{v1, v2}.
It follows:
v1 is redundant because v1 ∈ Span{u1, u2},
v2 is redundant because v2 ∈ Span{u1, u2}.
or
v1 is a linear combination of u1 and u2, v2 is a linear combination of u1 and u2.
If S = Span{u, v, w}, is there redundancy? In other words can be drop on of them from the list and S remains the same? Yes,
if u = αv + βw (u, v, w ≠ 0).
Rewrite:
αv + βw - u = 0.
Then 0 is a linear combination of v, u, w. We say that they are "linearly dependent".
Definition. Vectors x1,...., xs are said to be linearly dependent if there exists a linear combination, with not all zero coefficients, of them equal to zero. Otherwise, they are said to be linearly independent.
Example. s = 2. Two vectors x1 and x2 are linearly dependent when
αx1 + βx2 = 0, (α, β ≠ 0)
Solving for x1,
x1 = -(β/α)x2.
Therefore, x1 is a multiple of x2 and vice versa.
Example. s = 3. Three vectors u, v, w are linearly dependent:
αu + βv + γw = 0,
then we can solve for u:
u = -(βv + γw)/α = -(β/α)v - (γ/α)w
Therefore, u is a linear combination of v and w.
Example. Are the vectors u = (1,1,0), v = (0,1,1), w = (1,1,1) linearly independent? To answer the question, we need to find α, β, γ such that
αu + βv + γw = 0.
Rewrite:
α(1,1,0) + β(0,1,1) + γ(1,1,1) = 0
Thus we have 3 equations, for each of the coordinates:
α + γ = 0 α + β + γ = 0 β + γ = 0
We can solve the system, but we only case about this question: is there a non-zero solution. Answer: NO (verify). Hence, u, v and w are linearly independent.
Illustration here
Suppose S = Span{u, v, w}. If you can remove the vectors one at a time. Check if it is possible to write
Span{u, v, w} = Span{u, v} = Span{u, w} = Span{u}, etc.
If it is impossible then dim S = 3.
Example. Represent
R3 = Span{u,v,w} such that u, v, w are linearly independent.
The "standard unit vectors" are:
u = (1, 0, 0), v = (0, 1, 0), w = (0, 0, 1).
We need to prove two things:
1. R3 = Span{u,v,w}
Indeed, any vector is representable in terms of these three:
(a, b, c) = au + bv + cw.
Also
2. u, v, w are linearly independent.
Indeed, if
αu + βv + γw = 0
then
α(1,0,0) + β(0,1,0) + γ(0,0,1) = 0
hence
α = β = γ = 0.
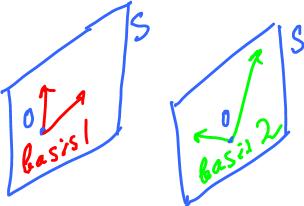
Definition. Given a vector space (or a linear subspace) S, then vectors v1, v2, ...., vn are called a basis of S if
1) S = Span{v1, v2, ...., vn}, and
2) v1, v2, ...., vn are linearly independent.
We also say that the dimension of S is n (the "the" part needs to be proven.).
Example. If S is a linear subspace with one basis {v1, v2}, then show that dim S = 2. Let us suppose there exists another basis {u1,... un} with say n = 3. In particular, it means that
Span{u1, u2, u3} = S.
We need to show that u1, u2, u3 are linearly dependent. Since {v1, v2} is a basis, we can write
u1 = αv1 + βv2 u2 = γv1 + δv2 u3 = λv1 + θv2
Next, we check linear independence u1, u2, u3 by investigating existence of scalars a, b, c such that
au1 + bu2 + cu3 = 0.
Rewrite:
a(αv1 + βv2) + b(γv1 + δv2) + c(λv1 + θv2) = 0 v1(aα + bγ + cλ) + v2(aβ + bδ + cθ) = 0
But, v1 and v2 are linearly independent. So,
aα + bγ + cλ = 0 and aβ + bδ + cθ = 0.
Solve this system.
This is a homogeneous system of equations in a, b, c and there is always a solution (0, 0, 0). If this system has a non-zero solutions for a, b, c, then u1, u2, u3 are linearly dependent.
The definition implies the following.
Theorem. If dimS = n, then any collection of linearly independent vectors has at most n elements.
If a subspace S has a basis {v1, v2,.... vn} and also another basis {u1, u2,..... um}, then, by the theorem, m ≤ n but also m = n or m ≥ n. Hence m = n.
Theorem. All bases of S must have same number of elements.
This implies that dimension of S is well defined.
Suppose, B = {u1, u2,.... un}is a basis of S . Further suppose,
x = a1u1 + a2u2 + .... + anun ______ (1) and also x = b1u1 + b2u2 + .... + bnun ______ (2).
Subtracting both sides of equation (2) from both sides of equation (1), we obtain
(a1 - b1)u1 + (a2 - b2)u2 + .... + (an - bn)un = 0
Since, B = {u1, u2,.... un} is a basis of S so its elements, i.e. u1, u2,.... un must be linearly independent. Therefore,
a1 - b1 = 0, a2 - b2 = 0, ...., an - bn = 0, i.e. a1 = b1, a2 = b2, ...., an = bn.
Hence,
Theorem. If B is a basis of S then every element of S is represented by a unique linear combination of the elements of B.
For this uniqueness, it makes sense to call a1, a2, ...., an the coordinates of x with respect to B:
x = (a1, a2, ...., an)
Definition. If A is an affine subspace then its dimension is defined as
dim A = dim S,
when A = z + S and S is a linear subspace.
Recall, if A = z + S = u + T, then S = T. So the dimension of A is well defined.
Theorem. Suppose, S' is a proper subspace of S. Then, dim S' < dim S.
Indeed, suppose S ≠ S'. Then there is x∈S\S'. Then let
T = Span(S' ∪ {x}).
Therefore according to the theorem, dim S' < dim T (since x ≠ 0).
This idea helps us with the next topic.
Building a basis
How do we build a basis for a subspace S of R'n? This is the procedure:
Pick x1∈S\{0};
Pick x2 ∈ S \ Span{x1} => dim span{x1, x2} = 2;
..
continue (induction)
..
Pick xk ∈ S \ Span{x1, x2,... xk-1} => dim {x1, x2,... xk} = k;
..
continue
..
Pick xn ∈ S \ Span{x1, x2,... xn-1} => dim {x1, x2,... xn} = n.
Stop
This happens when we can't pick
xn+1 ∈ S \ Span{x1, x2, ..... xn}
which is empty.
Definition. If S' is an affine subspace of S and dim S' = dim S - 1 then S' is called a hyperplane in S.
In R3, any plane is a hyperplane.
Theorem. S is a hyperplane in R3 iff S is the solution of a linear equation
a1x1 + a2x2 + ..... + anxn = b.
where not all of a1, a2,.... an are zero.
Review example. Suppose
S = {(x1, x2, x3): x2 = 0}.
Find an equation that represents S. Simple:
S = {(x1, 0, x3)}
Now, find an affine subspace A parallel to S and passing through z = (-3, 7, 4). Recall,
A = z + S, for any z ∈ A.
Compute:
A = z + {(x1, 0, x3)}
= {(-3, 7, 4) + (x1, 0, x3)}
= {(x1 -3, 7, x3 + 4)}.
So, S is shifted 7 units to the right.
How about a different example? Consider functions: {1, x, x2, x3}. Is this set linearly independent?
a0 + a1x + a2x2 + a3x3 = 0.
Since this holds for all x, this polynomial is the zero polynomial:
a0 = a1 = a2 = a3.
So, the answer is Yes. For more see Function spaces.