Cell decomposition of images

Redirect to:

• Cubical chains

Digital images: graphs or tiles?

A binary image is a combination of black and white pixels. Normally, it is assumed that objects are black and the background is white.

Now, how do you represent these objects? Each pixel is given by its location in the image, so it is just a pair of numbers. It seems natural to represent the object simply as a list of pairs of numbers and this is the way it is commonly done. We will follow this convention.

Beyond this, combinatorial, issue however the question is how to think of pixels geometrically.

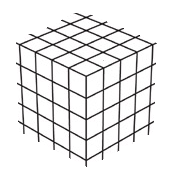
The common view is that pixels are dots, "pixel-dots". The pixel-dots are located on a grid:

Next, to study topology the image one has to understand how these dots form objects. This requires the notion of adjacency among pixel-dots. If two pixel-dots are "adjacent" they are connected by an edge, as in these pictures:

The result is a graph representation of binary images.

This seems simple enough. However, it turns out that the decision which nearby pixel-dots are adjacent isn't obvious. Should they be connected only along the grid? Or should the adjacency works diagonally as well? These two approaches are called the $4$-connectivity and the $8$-connectivity respectively. As you can see, we have:

• in the case of $4$-connectivity each pixel has $4$ neighbors, and
• in the case of $8$-connectivity each pixel has $8$ neighbors.

One might start to become concerned once you realize that you can't choose $4$-connectivity over $8$-connectivity or vice versa. Both are equally legitimate!

One may hope that choosing one of the two and sticking with it will provide a solid foundation for image analysis. The trouble starts when one considers the complement of an object represented by pixel-dots. One would expect that the complement should also be an object represented by pixel-dots based on the same adjacency relation. Consider this picture however.

If adjacency goes diagonally then A and D are connected to each other. Then B and C are not connected, so adjacency does not go diagonally. Wait a minute...

Exercise. Show that the Jordan theorem fails in this setting.

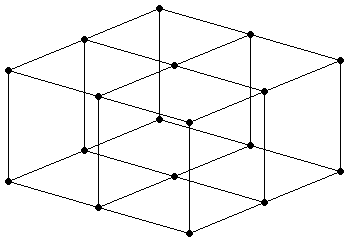
Things don't get any simpler as you more to higher dimensions:

Exercise. List all possible ways to define adjacency in 3d.

Let's take the Euclidean" view instead:

the universe is a continuum.

This view is traditional and mathematically solid.

Practically:

We think of pixels as tiles. We think of voxels as bricks.

Why? Because we want to break this continuous universe into small discrete pieces.

This is how the object in the image above can be represented with tiles:

Since these pieces are discrete, we can study the universe with computers. On the other hand, put together these "pixel-tiles" form a continuum. This continuum can be studied with the tools accumulated over the last $2$ thousand years:

• Euclidean geometry,
• Newtonian physics and calculus, etc.

A mathematical advantage is that, in the most general case, the shapes of these tiles may be different. They may be squares, triangles, hexagons, etc, as in a "tessellation". In fact, the shapes may vary within the same image. The shapes of cells may even be curved; the approach remains valid. Generally, these tiles, and bricks, are called cells.

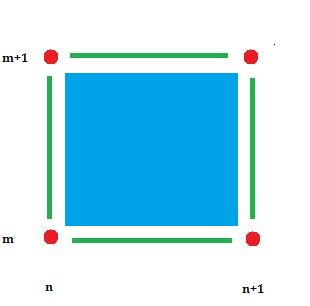
• A pixel becomes a square: $[n, n + 1] \times [m, m + 1]$.
• A voxel becomes a cube: $[n, n + 1] \times [m, m + 1] \times [k, k + 1]$.

To summarize: the euclidean space is cut into pieces and these pieces can be glued together and the original space reappears intact.

However this isn't the end of the story. Questions remain, such as: are lines also made of pixels?

Curves and surfaces

Curves made of pixels, or dots, produce pictures like this:

It is "non-Euclidean" because curves should be $1$-dimensional!

This a mismatch of the dimensions appears in 3D if you use voxels to make surfaces.

An idea of how to deal with this problem is suggested by the fact that the plane, which is just an example of a surface, is made of squares. Therefore, all surfaces should be made of squares too.

The next step is to realize that curves should be made of edges. A "digital", but Euclidean, curve will look like this:

This realization necessitates augmenting our collection of cells with cells of dimensions lower than that of the space itself.

This idea isn't entirely surprising as the second image below shows:

So, given a $2$-dimensional grid, we define (closed) cells for all integers $n,m$ as follows:

• a vertex is $\{ n\} \times \{ m\}$;
• an edge is $\{n \} \times [m, m + 1]$ or $[n, n + 1] \times \{m \}$;
• a pixel is $[n, n + 1] \times [m, m + 1]$.

This approach also gives us a uniform terminology for all dimensions:

• a vertex is a $0$-cell,
• an edge is a $1$-cell,
• a pixel is a $2$-cell,
• a voxel is a $3$-cell,
• etc.

Now that the geometric picture is clear, we need to find a consistent way of treating the boundaries of pixels. This is important because pixels are attached to each other along their boundaries - that's how they form objects!

Consider the cell decomposition of the pixel below. Observe that the edges and vertices may be shared with adjacent pixels:

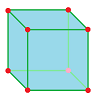
The cell decomposition of the voxel follows. The faces, edges, and vertices may be shared:

The result of a cell decomposition is what we call a cubical complex, or, more generally, a cell complex.

Boundaries and adjacency

The way to address this issue is suggested by the list above. The boundary of a voxel consists of $6$ faces, the boundary of the pixel consists of $4$ edges, the boundary of the edge consists of $2$ vertices. Therefore the decomposition of the image will contain all of these entities.

Note that we are not suggesting to every pixel is decomposed into a square, $4$ edges, and $4$ vertices. Edges and vertices are independent objects as they may be shared by adjacent pixels.

Cell decomposition of an image with 8 pixels arranged in a square:

One advantage of this approach is, once again, that it is uniform throughout all dimensions:

• The boundary of an edge, $1$-cell, consists of its two end-points, $0$-cells;
• The boundary a pixel, $2$-cell, consists of its four edges, $1$-cells;
• The boundary of a voxel, $3$-cell, consists of its six faces, $2$-cells;
• etc.

Now, we are on the solid ground to address adjacency. As the image is made of pixels, they are attached to each other along the edges they share. Again, this it is easily applicable to all dimensions:

• two adjacent edges, $1$-cells, share a vertex, $0$-cell;
• two adjacent pixels, $2$-cells, share an edge, $1$-cell;
• two adjacent voxels, $3$-cells, share a face, $2$-cell;
• etc.

Adjacent edges:

Adjacent pixels:

Adjacent voxels:

The hierarchy becomes clear.

Thus, our approach to image decomposition, in any dimension, boils down to the following:

The image is composed of cells in such a way that $k$-cells are attached to each other along $(k-1)$-cells.

Conveniently, the boundaries of the cells will make up the boundary of each object.

Images as cubical complexes

At this point we provide a formal definition of the main concept of cell decomposition in dimension $2$.

Any collection $γ$ of $0$-, $1$-, and $2$-cells is a cubical complex provided:

• if $γ$ contains an edge ($1$-cell) then γ contains its end points ($0$-cells) as well, and
• if $γ$ contains a face ($2$-cell) then γ contains its edges ($1$-cells) as well.

One typically refers to the cubical complex of the whole rectangle as the carrier.

Notice that a cubical complex is allowed to contain vertices and edges that are not parts of its faces. This allows us to use an incremental analysis algorithm that adds a pixel to the image by adding its vertices, edges, and face (in that order) and it is necessary to treat this collection of cells as a cubical complex at every step in the process.

Cell decomposition of the union of black pixels in a binary image produces a cubical complex. We will call it the cubical complex of the image.

This approach is applicable to any tessellation of images. A very common kind of cell decomposition occurs in mesh generation. Also, if we are given a disorganized "point cloud" (simply a collection of points in space), we think of it as a collection of vertices, or $0$-cells, in space. Then some of the points are connected by edges, $1$-cells. Finally, some triples of edges $AB, BC, CA$ produce triangles, or $2$-cells.

The approach can be easily extended to to higher dimensions. For more details, see Cubical complexes.

How do we deal with the topology and geometry of images?

The most dramatic advantage of this approach will become evident as we start doing algebra with cells. For that see Homology in 2D and Homology in 3D.

A more immediate consequence of the decision to rely on cell decomposition is the ability to use cycles and the simplification of the image analysis algorithm.

The cell decomposition also makes certain concepts more straightforward and familiar.

• First, an object and its background don’t share pixels, only edges. As a result, the area of a component plus the area of the complement is exactly equal to the total area of the image.
• Second, the perimeter is the number of edges in its boundary not the number of pixels.

So, the good new is that the geometry is the same as in high school.

One might find the areas found this way a bit surprising. Suppose we have a square and its corners are $(5,5)$, $(5,100)$, $(100,5)$ and $(100,100)$. Then the area should be $(100-5) \cdot (100-5)$, of course... Not for our approach! The correct result is $(100-5+1) \cdot (100-5+1)$. Why? Because all $4$ corner pixels (and their rows and columns) are included in the square. These pixels are tiles not just markers! (To see the advantage over the traditional formula, try to compute the area of a single pixel.)