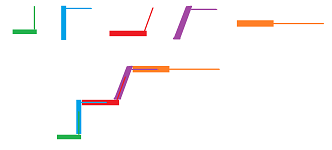This site is being phased out.
Geometry
Contents
The need for measuring in calculus
We will learn how to introduce an arbitrary geometry into the (so far) purely topological setting of cell complexes.
It is much easier to separate topology from geometry in the framework of discrete calculus because we have built it from scratch! For example, it is obvious that only the way the cells are attached to each other affects the matrix of the exterior derivative:
It is also clear that the sizes or the shapes of the cells are irrelevant.
However, even when those are given, the geometry of the domain will remain unspecified:
These grids can be thought of as different (but homeomorphic) realizations of the same cell complex.
In calculus, we rely only on the topological and algebraic structures to develop the mathematics. There are two main exceptions. One needs the dot product and the norm for the following two concepts:
- the concavity,
- the arc-length and the curvature.
The norm is explicitly present in the formulas for the latter. In fact, the example above shows that to introduce the curvature one will need to add more structure -- geometric in nature -- to the complex.
The role of geometry in the former is less explicit.
The point where we start to need geometry is when we move from the first to the second derivative.
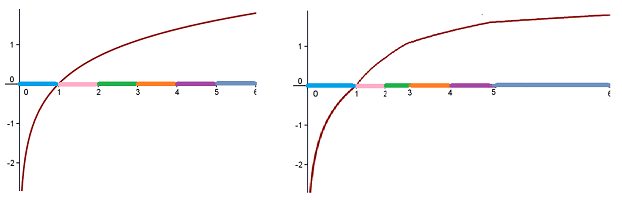
This is what we observe: shrinking, stretching, or deforming the $x$- or the $y$ axes won't change the monotonicity of a function but it will change its concavity.
For example, here we have deformed the $x$-axis and changed the concavity of the graph at $x=1$:
Of course, it is sufficient to know the sign of the derivative to distinguish between increasing and decreasing behavior. Therefore, this behavior depends only on the topology of the spaces, in the above sense. Indeed, the chain rule implies the following elementary result.
Proposition. Given a differentiable function $f:{\bf R}\to {\bf R}$, $$f\nearrow\ \Longleftrightarrow\ fr\nearrow,$$ for any differentiable $r:{\bf R}\to {\bf R}$ with $r'>0$,
Exercise. Give an example of $f$ and $r$ as above so that $f$ and $fr$ have different concavity.
Similarly, in the discrete calculus we are developing, the sign of the exterior derivative will tell us the difference between increasing and decreasing behavior. But the derivative only uses the topological properties of the complex!
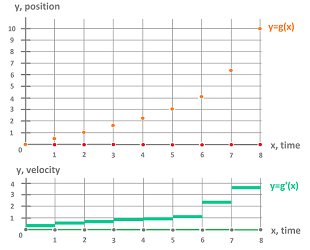
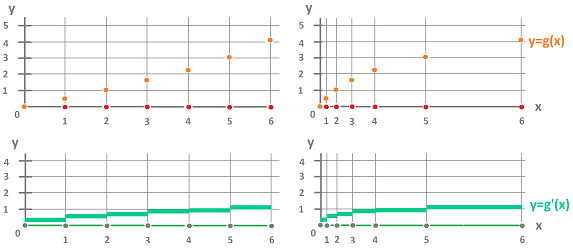
Concavity is an important concept that captures the shape of the graph of a function in calculus as well as the acceleration in physics. The upward concavity of the discrete function below is obvious, which reflects the positive acceleration:
The concavity is computed and studied via the second derivative, the rate of change of the rate of change. But, with $dd=0$, we don't have the second exterior derivative!
We start from scratch and look at the change of change. This quantity can be seen algebraically as the increase of the exterior derivative (i.e., the change): $$g(2)-g(1) < g(3)-g(2),\ g(3)-g(2) < g(4)-g(3),\ etc.$$ However, does this algebra imply concavity? Not without assuming that the intervals have equal lengths!
Below, on the same, topologically, cell complex, we have the same discrete function with, of course, the same exterior derivative:
...but with the opposite concavity!
Inner products
In order to develop a complete discrete calculus we need to be able compute:
- the lengths of vectors and
- the angles between vectors.
In linear algebra, we learn how an inner product adds geometry to a vector space. We choose a more general setting.
Suppose $R$ is our ring of coefficients and suppose $V$ is a finitely generated free module over $R$.
Definition. An inner product on $V$ is a function that associates a number to each pair of vectors in $V$: $$ \langle \cdot,\cdot \rangle :V \times V \to R;$$ $$(u,v) \mapsto \langle u,v \rangle ,\ u,v \in V,$$ that satisfies these properties:
- 1.
- $ \langle v,v \rangle \geq 0$ for any $v \in V$ -- non-degeneracy,
- $ \langle v,v \rangle =0$ if and only if $v=0$ -- positive definiteness;
- 2. $ \langle u , v \rangle = \langle v,u \rangle $ -- symmetry (commutativity);
- 3. $ \langle ru,v \rangle =r \langle u ,v \rangle $ -- homogeneity;
- 4. $ \langle u + u ' ,v \rangle = \langle u ,v \rangle + \langle u ' ,v \rangle $ -- distributivity.
Items 3 and 4 together make up bi-linearity. Indeed, consider $p: V \times V \to R$, where $p ( u , v)= \langle u , v \rangle $. Then $p$ is linear with respect to the first variable, and the second variable, separately:
- 1) fix $v=b$, then $p(\cdot,b)$ is linear: $V \to R$;
- 2) fix $u=a$, then $p(a,\cdot)$ is linear: $V \to R$.
Exercise. Show that this isn't the same as linearity.
It is easy to verify these axioms for the dot product defined on $V={\bf R}^n$ or any other module with a fixed basis. For $$u=(u_1,...,u_n),\ v=(v_1,...,v_n) \in {\bf R}^n,$$ let $$ \langle u , v \rangle :=u_1v_1 + u_2v_2 + ... + u_nv_n .$$ Moreover, a weighted dot product on ${\bf R}^n$ is given by: $$ \langle u , v \rangle :=w_1u_1v_1 + w_2u_2v_2 + ... + w_nu_nv_n ,$$ where $w_i \in {\bf R} ,\ i=1,...,n$, are the positive “weights”, is also an inner product.
Exercise. Prove the last statement.
A module equipped with an inner product is called an inner product space.
When ring $R$ is a subring of the reals ${\bf R}$, such as the integers ${\bf Z}$, we can conduct some useful computations.
Definition. The norm of a vector $v$ in an inner product space $V$ is defined as $$\lVert v \rVert:=\sqrt { \langle v,v \rangle }\in {\bf R}.$$
This number measures the length of the vector.
Definition. The angle between vectors $u,v \ne 0$ in $V$ is defined by this familiar formula: $$\cos \widehat{uv} = \frac{ \langle u, v \rangle }{ \lVert u \rVert \cdot \lVert v \rVert }.$$
The norm satisfies certain properties that we can also use as axioms of a normed space.
Definition.Given a vector space $V$, a norm on $V$ is a function $$\lVert\cdot \rVert:V \to R$$ that satisfies
- 1.
- $\lVert v \rVert \geq 0$ for all $v \in V$,
- $\lVert v \rVert = 0$ if and only if $v=0$;
- 2. $\lVert rv \rVert = |r| \lVert v \rVert$ for all $v \in V, r\in R$;
- 3. $\lVert u + v \rVert \leq \lVert u \rVert + \lVert v \rVert$ for all $u, v \in V$.
Proposition. A normed space is a metric space with the metric $d(x,y):=\lVert x-y \rVert.$
Exercise. Prove that the inner product is continuous in this metric space.
This is what we know from linear algebra.
Theorem. Any inner product $ \langle \cdot, \cdot \rangle $ on an $n$-dimensional module $V$ can be computed via matrix multiplication $$ \langle u, v \rangle =u^T Q v,$$ where $Q$ is some positive definite, symmetric $n \times n$ matrix.
In particular, the dot product is represented by the identity matrix $I_n$, while the weighted dot product is represented by the diagonal matrix: $$Q=\operatorname{diag}[w_1,...,w_n].$$
To emphasize the source of the norm we may use this notation: $$\lVert v \rVert _Q =\sqrt { \langle v,v \rangle } = \sqrt {v^T Q v}.$$
Below we assume that $R={\bf R}$.
To learn about the eigenvalues and eigenvectors of this matrix, we observe that $$\lVert v \rVert _Q ^2 =v^T Q v = v^T \lambda v = \lambda \lVert v \rVert ^2,$$ where $\lVert v \rVert$ is the norm generated by the dot product. We have proven the following.
Theorem. The eigenvalues of a positive definite matrix are real and positive.
We know from linear algebra that if the eigenvalues are real and distinct, the matrix is diagonalizable. As it turns out, having distinct eigenvalues isn't required for a positive definite matrix. We state the following without proof.
Theorem. Any inner product $ \langle \cdot, \cdot \rangle $ on an $n$-dimensional vector space $V$ can be represented, via a choice of basis, by a diagonal $n \times n$ matrix $Q$ with positive numbers on the diagonal. In other words, every inner product is a weighted dot product, in some basis.
Also, since the determinant $\det Q$ of $Q$ is the product of the eigenvalues of $Q$, it is also positive and we have the following.
Theorem. Matrix $Q$ that represents an inner product is invertible.
The metric tensor
What if the geometry -- as described above -- varies from point to point in some space $X$? Then the inner product of two vectors will depend on their location.
In fact, we'll need to look at a different set of vectors in each location as the angle between two vectors is meaningless unless they have the same origin.
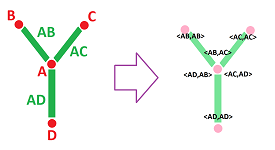
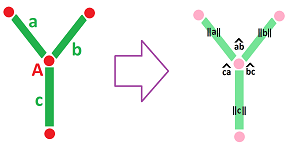
We already have such a construction! For each vertex $A$ in a cell complex $K$, the tangent space at $A$ of $K$ is a submodule of $C_1(K)$ generated by the $1$-dimensional star of the vertex $A$: $$T_A(K):=< \{AB \in K\} > \subset C_1(K).$$
However, the tangent bundle $T_1(K)$ is inadequate because this time we need to consider two directions at a time!
Since $V=T_A$ is a module, an inner product can be defined, locally. Then we have a collection of bi-linear functions for each of the vertices, $$\psi_A: T_A(K)^2\to R,\ A\in K^{(0)}.$$ The setup is as follows. We have the space of locations $X=K^{(0)}$, the set of all vertices of a cell complex $K$, and, second, to each location $A\in X$, we associate the space of pairs of directions $T_A(K)^2$. We now collect these “double” tangent spaces into one.
Definition. The tangent bundle of degree $2$ of $K$ is defined to be: $$T_2(K):=\bigsqcup _{A\in K} \left( \{A\} \times T_A(K)^2 \right).$$
Then a locally defined inner product is seen as a function on this space, $$\psi =\{\psi_A\}:T_2(K) \to R,$$ bi-linear on each tangent space, defined by $$\psi (A,AB,AC):=\psi_A(AB,AC).$$ In other words, we have inner products “parametrized” by location.
Furthermore, we have a function that associates to each location, i.e., a vertex $A$ in $K$, and each pair of directions at that location, i.e., edges $x=AB,y=AC$ adjacent to $A$ with $B,C\ne A$, a number $ \langle AB, AC \rangle $: $$(A,AB,AC) \mapsto \langle AB, AC \rangle (A) \in R.$$
Note: we have used the same notation for $f(a)=\langle f,a \rangle$, where $f$ is a form, but won't use it in this section.
We have created an inner product “parametrized” by location.
Definition. A metric tensor on a cell complex $K$ is a collection of functions, $$\psi=\{\psi_A:\ A\in X\},$$ such that each of them, $$\psi_A: \{A\} \times T_A(K)^2 \to R,$$ satisfies the axioms of inner product, and also: $$ \psi_A (AB,AB) = \psi_B (BA,BA).$$
Using our notation, a metric tensor is such a function: $$ \langle \cdot,\cdot \rangle (\cdot): T_2(K) \to R,$$ that, when restricted to any tangent space $T_A(K),\ A\in K^{(0)}$, it produces a function $$ \langle \cdot,\cdot \rangle (A): T_A(K)^2 \to R,$$ which is an inner product on $T_A(K)$. The last condition, $$ \langle AB,AB \rangle (A) = \langle BA,BA \rangle (B),$$ ensures that these inner products match!
Note. The location space $X$ may be an $n$-manifold; then $T_AX\cong {\bf R}^n$ is its tangent space, when $R={\bf R}$. Then we have a function that associates a number to each location in $X$ and each pair of vectors at that location: $$ \langle \cdot,\cdot \rangle (\cdot): X \times {\bf R}^n \times {\bf R}^n \rightarrow {\bf R},$$ $$(x,u,v) \mapsto \langle u, v \rangle (x) \in {\bf R}.$$ It is an inner product at each location $x \in X$ that depends continuously on $x$.
Exercise. Provide the details of the axioms of inner product (non-degeneracy, positive-definiteness, symmetry, homogeneity, and distributivity) for the metric tensor.
The end-result is similar to a combination of forms, as we have a number assigned to each edge and to each pair of adjacent edges:
- $a \mapsto \langle a, a \rangle $;
- $(a,b) \mapsto \langle a, b \rangle $.
Then the metric tensor is given by the table of its values for each vertex $A$: $$\begin{array}{c|ccccccccc} A & AB & AC & AD &...\\ \hline AB & \langle AB,AB \rangle & \langle AB,AC \rangle & \langle AB,AD \rangle &...\\ AC & \langle AC,AB \rangle & \langle AC,AC \rangle & \langle AC,AD \rangle &...\\ AD & \langle AD,AB \rangle & \langle AD,AC \rangle & \langle AD,AD \rangle &...\\ ...& ... & ... & ... &... \end{array} $$
Whenever our ring of coefficients happens to be a subring of the reals ${\bf R}$, such as the integers ${\bf Z}$, this data can be used to extract more usable information:
- $a \mapsto \lVert a \rVert$;
- $(a,b) \mapsto \widehat{ab}$, where
$$\cos\widehat{ab} = \frac{ \langle a, b \rangle }{\lVert a \rVert \lVert b\rVert}.$$
We have all the information we need for measuring in this symmetric matrix: $$\begin{array}{c|ccccccccc} A & AB & AC & AD &...\\ \hline AB & \lVert AB \rVert & \widehat{BAC} & \widehat{BAD} &...\\ AC & \widehat{BAC} & \lVert AC \rVert & \widehat{CAD} &...\\ AD & \widehat{BAD} & \widehat{CAD} & \lVert AD \rVert &...\\ ...& ... & ... & ... &... \end{array} $$
Exercise. In the $1$-dimensional cubical complex ${\mathbb R}$, are $01$ and $10$ parallel?
Proposition. From any matrix with positive entries on the diagonal, we can (re)construct a metric tensor by the formula: $$ \langle AB , AC \rangle =\lVert AB \rVert\lVert AC \rVert\cos\widehat{BAC}.$$
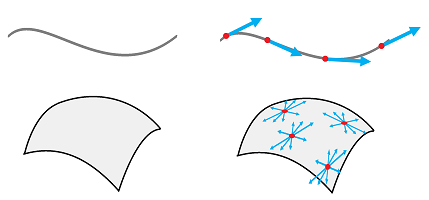
With a metric tensor, we can define the two main geometric quantities of calculus, in a very easy fashion. Suppose we have a discrete curve $C$ in the complex $K$, i.e., a sequence of adjacent vertices and edges $$C:\quad A_0,A_1,...,A_N \in K \quad \& \quad A_0A_1,A_1A_2,...,A_{N-1}A_N\in K.$$
Definition. The arc-length of curve $C$ is the sum of the lengths of its edges: $$l_C:=\lVert A_0A_1 \rVert + \lVert A_1A_2 \rVert +... + \lVert A_{N-1}A_N \rVert.$$
The arc-length is an example of a line integral of a $1$-form $\rho$ over a $1$-chain $a$ in complex $K$ equipped with a metric tensor: $$\begin{array}{ll} a=&A_0A_1+A_1A_2+...+A_{n-1}A_n \Longrightarrow \\ &\int_a \rho:= \rho (A_0,A_0A_1)\lVert A_0A_1 \rVert+... +\rho (A_{N-1},A_{N-1}A_N)\lVert A_{N-1}A_N \rVert. \end{array}$$ In particular, if we have a curve made of rods represented by edges in our complex and if $\rho$ represents the linear density of each rod, then the integral gives us the weight of the curve.
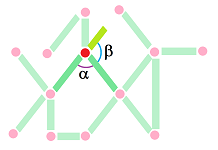
For the curvature, the angle $\alpha:=\widehat{A_{s-1}A_sA_{s+1}}$ might appear a natural choice to represent it, but, since we need to capture the change of the direction, it should be the “outer” angle $\beta$:
Definition. The curvature of curve $C$ at a given vertex $A_s,\ 0<s<N,$ is the value of the angle $$\kappa _C (A_s):=\pi-\widehat{A_{s-1}A_sA_{s+1}}.$$
Again, the result depends on our choice of a metric tensor.
Metric tensors in dimension 1
Let's consider examples of how adding a metric tensor turns a cell complex, which is a discrete representation of a topological space, into something more rigid.
We assume below that our cell complex $K$ is equipped with a metric tensor $\langle\cdot , \cdot\rangle$.
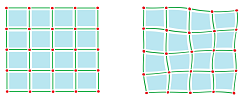
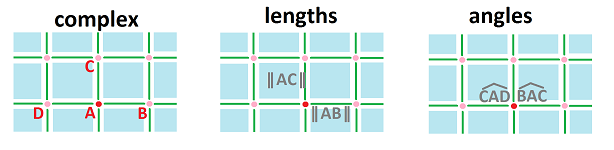
Example. In the illustration below you see the following:
- a cubical complex $K$, a topological entity: cells and their boundaries also made of cells;
- complex $K$ combined with a choice of metric tensor $\langle \cdot,\cdot \rangle$, a geometric entity: lengths and angles;
- a realization of $K$ in ${\bf R}$ as a segment;
- a realization of $K$ in ${\bf R}^2$;
- another realization of $K$ in ${\bf R}^2$.
The three realizations are homeomorphic but they differ geometrically, even though the last two have the same lengths and angles.
$\square$
Definition. A (geometric) realization of dimension $n$ of a cell complex $K$ equipped with a metric tensor $\langle \cdot,\cdot \rangle$ is a realization $|K|\subset {\bf R}^n$ of $K$ such that the Euclidean metric tensor of ${\bf R}^n$ matches $\langle \cdot,\cdot \rangle$.
In the example above we see a $1$-dimensional cell complex with two different geometric realizations of dimension $2$.
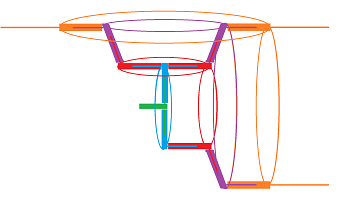
There is even more room of variability if we consider realizations in ${\bf R}^3$. Indeed, even with fixed angles one can rotate the edges freely. To illustrate this idea, we consider a mechanical interpretation of a realization. We think of $|K|$ as if it is constructed of pieces in such a way that
- each edge is a combination of a rod and a tube attached to each other, and
- at each vertex, a rod is inserted into the next tube.
The rods are free to rotate – independent of each other -- while still preserving the lengths and angles:
We are after only the intrinsic geometric properties of these objects just as elsewhere we study intrinsic topological properties. Recall that you can detect those properties while staying inside the object.
Example. In a $1$-dimensional complex, one can think of a worm moving through a tube. The worm can only feel the distance that it has passed and the angle (but not the direction) at which its body bends:
Meanwhile, we can see the whole thing by stepping outside, to the second dimension.
But, can the worm tell a left turn from a right?
$\square$
The ability to rotate these rods allows us to make the curve flat! This observation underscores the fact that a metric tensor may not represent the geometry unambiguously.
Exercise. (a) Provide metric tensors for a triangle, a square, and a rectangle. (b) Approximate a circle.
A metric tensor can also be thought of as a pair of maps:
- $AB \mapsto \lVert AB \rVert$;
- $(AB,AC) \mapsto \widehat{BAC}$.
This means that in the $2$-dimensional case there will be one (positive) number per edge and six per vertex. To simplify this a bit, below we assume that the opposite angles are equal. This is a type of local symmetry that allows us to work with just two numbers per vertex and yet allows for a sufficient variety of examples.
We can illustrate metric tensors by specifying the lengths and the angles:
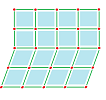
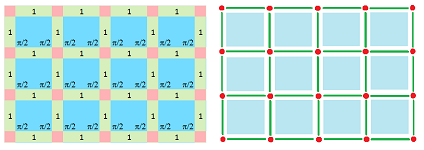
In the examples below, we put the metric data on the left over the complete cubical complex for the whole grid and then use it as a blueprint to construct its realization as a rigid structure, on the right. The $2$-cells are ignored for now.
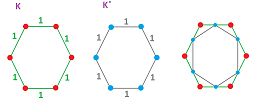
Example (square grid). This is the standard “geometric” cubical complex ${\mathbb R}^2$:
$\square$
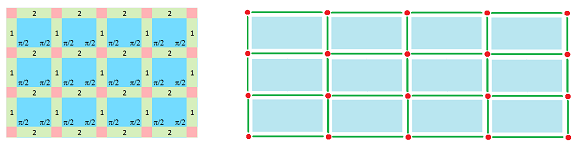
Example (rectangular grid). This is ${\mathbb R}^2$ horizontally stretched:
$\square$
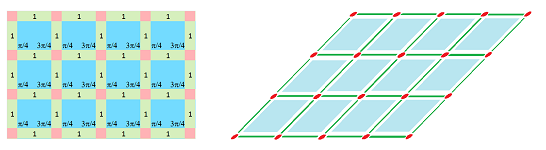
Example (rhomboidal grid). This is ${\mathbb R}^2$ stretched in the diagonal direction:
$\square$
Exercise. Provide a realization for a grid with lengths: $1,1,1,...$, and angles: $\pi/2,\pi/4,\pi/2,...$.
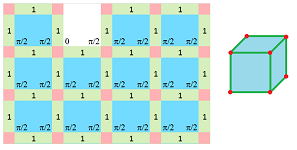
Example (cubical grid). We want the $3$-space subdivided into cubes by these squares:
Here we don't assume anymore that the opposite angles are equal, nor do we use the whole grid.
$\square$
Exercise. Provide the rest of the realization for the last example.
Exercise. Provide a metric tensor complex for a cube.
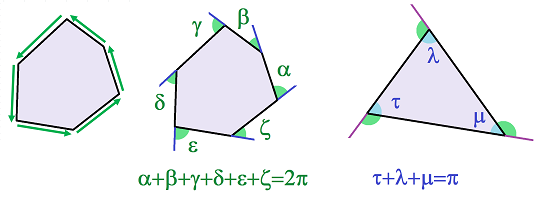
Suppose we have a discrete closed curve $C$ in the complex $K$ : $$C:\quad A_0,A_1,...,A_N=A_0 \in K \quad \& \quad A_0A_1,A_1A_2,...,A_{N-1}A_N\in K.$$ The total curvature of curve $C$ is the sum of the curvatures: $$\kappa _C :=\sum_{s=1}^N\kappa _C (A_s):=\sum_{s=1}^N(\pi-\widehat{A_{s-1}A_sA_{s+1}}).$$
Theorem. Suppose a cubical or simplicial complex is realized in the plane and suppose a polygon is bounded by a closed discrete curve in this complex. Then the total curvature is equal to $2\pi$.
Exercise. Prove the theorem.
In the case of a triangle, the sum of the inner angles is $3\pi$ minus the former. We have proved the following theorem familiar from middle school.
Corollary (Sum of Angles of Triangle). It is equal to $180$ degrees.
Geometric complexes in dimension 1
Let's consider again the $1$-dimensional complex $K$ from the last subsection. With all of those rotations possible, how do we make this construction even more rigid?
We start by considering another mechanical interpretation of a geometric realization $|K|$:
- we think of edges as rods and vertices as hinges.
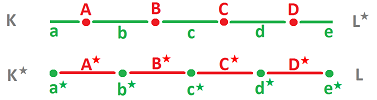
Then there is another way to make the angles of the hinges fixed: we can connect the centers of the adjacent rods using an extra set of rods. These rods (connected by a new set of hinges) form a new complex $K^{\star}$.
Exercise. Assume that the vertices of the new complex are placed at the centers of the edges. (a) Find the rest of the lengths. (b) Find the angles too. (c) Find a metric tensor for $K^\star$.
The cells of the two complexes are matched:
- an edge $a$ in $K$ corresponds to a vertex $a^\star$ in $K^\star$; and
- a vertex $A$ in $K$ corresponds to an edge $A^\star$ in $K^\star$.
Furthermore, the correspondence can be reversed!
Then, we have a one-to-one correspondence between the original, called primal, cells and the dual cells: $$\begin{align*} 1\text{-cell (primal)} &\longleftrightarrow 0\text{-cell (dual)} \\ 0\text{-cell (primal)} &\longleftrightarrow 1\text{-cell (dual)} \end{align*}$$ The combined rule is for $k=0,1$:
Next, we assemble these new cells into a new complex:
Given a complex $K$, the set of all of the duals of the cells of $K$ is the new complex $K^{\star}$.
Definition. Two cell complexes $K$ and $K^{\star}$ are called Hodge-dual of each other if there is a one-to-one correspondence between the $k$-cells of $K$ and $(1-k)$-cells of $K^\star$, for $k=0,1$.
Notation. To avoid confusion between the familiar duality between vectors and covectors (and chains and cochains) known as the “Hom-duality” and the new Hodge-duality, we will use the star $\star$ instead of the usual asterisk $*$.
Exercise. Define the boundary operator of the dual grid in terms of the boundary operator of the primal grid, in dimension $1$.
What kinds of complexes are subject to this construction?
Suppose $K$ is a graph and its vertex $A$ has three adjacent edges $AB,AC,AD$. Then, in the dual complex $K^\star$, the edge $A^\star$ is supposed to join the vertices $AB^\star,AC^\star,AD^\star$. This is impossible, and, therefore, such a complex has no dual.
Then,
- both $K$ and $K^\star$ have to be curves.
Furthermore, once constructed $K^{\star}$ doesn't have to be a cell complex as some of the boundary cells may be missing. For example, the dual of a single vertex complex $K=\{A\}$ is a single edge “complex” $K^{\star}=\{A^{\star}\}$. The end-points of this edge aren't present in $K^\star$. This is a typical example of the dual of a “closed” complex being an “open” complex. Such a complex won't have the boundary operator well-defined.
What's left? The complex $K$ has to be a complex representation of the line or the circle: $${\mathbb R}^1 \ \text{or} \ {\mathbb S}^1 ,$$ or their disjoint union.
In other words, they are $1$-dimensional manifolds without boundary.
Proposition. $$\left( {\mathbb R}^1 \right)^\star ={\mathbb R}^1,\quad \left( {\mathbb S}^1 \right)^\star ={\mathbb S}^1 .$$
Exercise. Prove the proposition.
Up to this point, the construction of the dual $K^\star$ has been purely topological. The geometry comes into play when we add a metric tensor to the picture.
Definition. A geometric cell complex of dimension $1$ is a pair of a $1$-dimensional cell complex $K$ and its dual $K^{\star}$, either equipped with a metric tensor.
Note that “dimension $1$” doesn't refer to the dimension of the complex $K$ but rather the ambient dimension of the pair complex: $$1=\dim a+\dim a^\star.$$
Notation. Instead of $||AB||$, we use $|AB|$ for the length of $1$-cell $AB$. The latter notation will be used for the “volumes” of cells of all dimensions, including vertices.
Hodge duality is a correspondence between cells of the two complexes, what about chains?
S we have dome many times, we can extend this correspondence by linearity from cells to chains producing an operator with the identity matrix. Instead, we choose to incorporate the geometry of the complex into this new map.
Definition. The (chain) Hodge star operator of a geometric complex $K$ is the pair of homomorphisms on chains of complementary dimensions: $$\star:C_k(K)\to C_{1-k}(K^\star ),\ k=0,1,$$ $$\star:C_k(K^\star)\to C_{1-k}(K),\ k=0,1,$$ defined by $$\star (a)=\frac{|a|}{|a^\star|}a^\star.$$ for any cell $a$, dual or primal, under the convention: $$|A|=1, \text{ for every vertex } A.$$
The choice of the coefficient of this operator is justified by the following crucial property.
Theorem (Isometry). The Hodge star operator preserves lengths: $$|\star (a)|=|a|.$$
Proposition. The matrix of the Hodge star operator $\star$ is diagonal with: $$\star_{ii}=\frac{|a_i|}{|a_i^\star|},$$ where $a_i$ is the $i$th cell of $K$.
Hodge duality of forms
What happens to the forms as we switch to the Hodge-dual complex?
Since $i$-forms are defined on $i$-cells, $i=0,1$, the matching of the cells that we saw,
- primal $i$-cell $\leftrightarrow$ dual $(1-i)$-cell,
produces a matching of the forms,
- primal $i$-form $\leftrightarrow$ dual $(1-i)$-form.
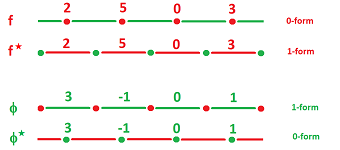
For example,
- If $f(A)=2$ for some $0$-cell $A$ in $K$, there should be somewhere a $1$-cell, say, $A^{\star}$ so we can have $f^\star(A^\star)=2$ for a new form $f^\star$ in $K^\star$.
- If $\phi(a)=3$ for some $1$-cell $a$, there should be somewhere a $0$-cell, say, $a^\star$ so we can have $\phi^\star(a^\star)=3$.
To summarize,
- if $f$ is a $0$-form then $f^{\star}$ is a $1$-form with the same values;
- if $\phi$ is a $1$-form then $\phi ^{\star}$ is a $0$-form with the same values.
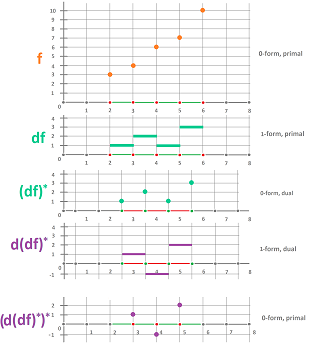
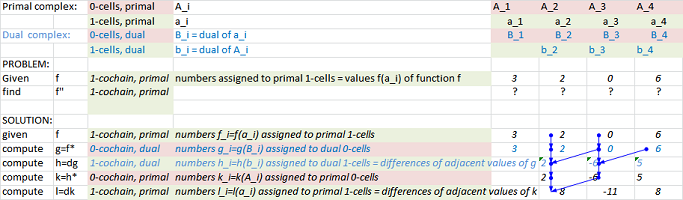
This is what is happening in dimension $1$, illustrated with Excel:
Link to the file: Spreadsheets.
Algebraically, if $f$ is a $0$-form over the primal complex, we define a new form by: $$f^{\star}(a):=f(a^{\star}).$$ for any $1$-cell $a$ in the dual complex. And if $\phi$ is a $1$-form over the primal complex, we define a new form by: $$\phi^{\star}(A):=\phi(A^{\star})$$ for any $0$-cell $A$ in the dual complex.
We put this together below.
Definition. In a geometric complex $K$, the Hodge-dual $\psi^\star$ of a form $\psi$ over $K$ is given by: $$\psi^{\star}(\sigma):=\psi(\sigma ^{\star}),$$ where
- $\psi$ is a $0$-form and $\sigma$ is a $1$-cell, or
- $\psi$ is a $1$-form and $\sigma$ is a $0$-cell.
This formula will used as the definition of duality of form of all dimensions.
Of course, the forms are extended from cells to chains by linearity making these diagrams commutative: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccc} &C_{k}(K)& \ra{\star} & C_{1-k}(K^\star) &&&C_{k}(K)& \la{\star} & C_{1-k}(K^\star) &&\\ &\ \ \da{\varphi} & &\ \ \da{\varphi^\star} && &\ \ \da{\psi^\star}& &\ \ \da{\psi} && \\ &R&= & R& &&R& =& R& & \end{array} $$ Then the formula can be written as: $$(\star \psi)(a):=\psi(\star a ),$$ where $\star$ in the right-hand side is the chain Hodge star operator, for any primal/dual cochain $\psi$ and any dual/primal chain $a$. We will use the same notation when there is no confusion.
Definition. The (cochain) Hodge star operator of a geometric complex $K$ is the pair of homomorphisms, $$\star :C^k(K)\to C^{1-k}(K^\star),\ k=0,1,$$ $$\star :C^k(K^\star)\to C^{1-k}(K),\ k=0,1,$$ defined by $$\star (\psi) :=\psi^{\star}.$$
In other words, the new, cochain Hodge star operator is the dual (Hom-dual, of course) of the old, chain Hodge star operator, i.e., $$\star=\star^*.$$
The diagonal entries of the matrix of the new operator are the reciprocals of that of the old.
Proposition. The matrix of the Hodge star operator is diagonal with $$\star_{ii}=\frac{|a^\star_i|}{|a_i|},$$ where $a_i$ is the $i$th cell of $K$.
Proof. From the last subsection we know that the matrix of the chain Hodge star operator, $$\star :C_k(K)\to C_{1-k}(K^\star),$$ is diagonal with $$\star_{ii}=\frac{|a_i|}{|a^\star_i|},$$ where $a_i$ is the $i$th cell of $K$. We also know that the matrix of the dual is the transpose of the original. Therefore, the matrix of the dual of the above operator, which is the cochain Hodge star operator, $$\star^* :C^{1-k}(K^\star)\to C^{k}(K),$$ is given by the same formula! We now restate this conclusion for the other cochain Hodge star operator, $$\star^* :C^k(K)\to C^{1-k}(K^\star).$$ We simply replace in the formula: $a$ with $a^\star$ and $k$ with $(1-k)$, producing the required outcome. $\blacksquare$
Exercise. Provide the formula for the exterior derivative of $K^\star$ in terms of that of $K$.
The first derivative
The geometry of the complex allows us to define the first derivative of a discrete function (i.e., a $0$-form) as “the rate of change” instead of just “change” (the exterior derivative).
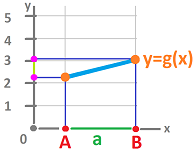
This is the definition from elementary calculus of the derivative of a function $g:{\bf R}\to {\bf R}$: $$g'(u) := \lim_{h\to 0}\frac{g(u+h)-g(u)}{h}= \lim_{v\to u}\frac{g(v)-g(u)}{v-u}.$$
Now, this is the setting of the discrete case for a $1$-dimensional complex $K$:
Then the discrete analogue of the first derivative above is $$\frac{g(B)-g(A)}{|AB|}.$$
Let's take a closer look at this formula. The numerator is easily recognized as the exterior derivative of the $0$-form $g$ evaluated at the $1$-cell $a=AB$. Meanwhile, the denominator is the length of this cell. In other words, we have: $$g'(a^\star):=\frac{dg(a)}{|a|}.$$ Then we define the derivative (not to be confused with $d$) as follows.
Definition. The first derivative of a primal $0$-form $g$ on a geometric cell complex $K$ is a dual $0$-form given by its values at the vertices of $K^\star$: $$g'(P):=\frac{dg(P^\star)}{|P^\star|}.$$ The form $g$ is called differentiable if this division makes sense in ring $R$.
Proposition. All forms are differentiable provided: $$\frac{1}{|a|}\in R$$ for every cell $a$ in $K$. In particular, this is the case under either of the two conditions below:
- the ring $R$ of coefficients is a field, or
- the geometry of the complex $K$ is trivial: $|AB|=1$.
The formula is simply the exterior derivative -- with the extra coefficient equal to the reciprocal of the length of this edge. We recognize this coefficient from the definition of the Hodge star operator $\star :C^k(K)\to C^{1-k}(K^\star),\ k=0,1$. It is given by a diagonal matrix with $$\star _{ii}=\frac{1}{|a_i|},$$ where $a_i$ is the $i$th $k$-cell of $K$ ($|A|=1$ for $0$-cells). Therefore, we have an alternative formula for the derivative.
Proposition. $$g'=\star d g.$$
Therefore, differentiation is a linear operator: $$\frac{d}{dx}=\star d:C^{0}(K) \to C^{0}(K^\star).$$ It is seen as the diagonal of the following Hodge star diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccc} g\in&C^{0}(K)& \ra{d} & C^1(K) &\\ && _{\frac{d}{dx}}\searrow & \da{\star} & \\ && & C^{0}(K^\star)& \ni g'\\ \end{array} $$
This is how the formula works in the case of edges with equal lengths:
Exercise. Prove: $f'=0\Rightarrow f=const$.
Exercise. Create a spreadsheet for computing the first derivative as the “composition” of the spreadsheets for the exterior derivative and the Hodge duality.
Exercise. Define the first derivative of a $1$-form $h$ and find its explicit formula. Hint: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccc} && & C^1(K) &\ni h\\ && ^{\frac{d}{dx}}\swarrow & \da{\star} & \\ h'\in &C^{1}(K^\star)& \la{d}& C^{0}(K^\star)& \\ \end{array} $$
The second derivative
The concavity of a function is determined by the sign of its second derivative, which is "the rate of change of the rate of change". In contrast to elementary calculus, it can be defined as a single limit: $$g' '(u) = \lim_{h\to 0}\frac{\frac{g(u+h)-g(u)}{h} - \frac{g(u)-g(u-h)}{h}}{h}.$$ It is important to notice here that the definition remains the same if $h$ is required to be positive!
Proposition. $$g' '(u) = \lim_{v-u=u-w\to 0+}\frac{\frac{g(v)-g(u)}{v-u} - \frac{g(u)-g(w)}{u-w}}{(w-v)/2}.$$
Exercise. Prove the proposition.
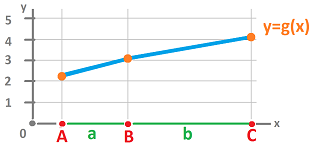
This is the setting of the discrete case:
Then the discrete analogue of the second derivative above is $$\frac{\frac{g(C)-g(B)}{|BC|} - \frac{g(B)-g(A)}{|AB|}}{|AC|/2}.$$
Let's take a closer look at this formula.
The two fractions in the numerator are easily recognized as the exterior derivative of the $0$-form $g$ evaluated at the $1$-cells $a$ and $b$ respectively. Meanwhile, the denominators are the lengths of these cells.
The denominator is, in fact, the distance between the centers of the cells $a$ and $b$. Therefore, we can think of it as the length of the dual cell of the vertex $B$. Then, we define the second derivative (not to be confused with $dd$) of a $0$-form $g$ as follows.
Definition. The second derivative of a primal $0$-form $g$ on a geometric cell complex $K$ is a primal $0$-form given by its values at vertices of $K$: $$g' '(B)=\frac{\frac{dg(b)}{|b|} - \frac{dg(a)}{|a|}}{|B^\star|},$$ where $a,b$ are the $1$-cells adjacent to $B$.
We take this one step further. First, we recognize both terms in the numerator as the first derivative $g'$, evaluated at $a$ and $b$. What about the difference? Combined with the denominator, it is the derivative of $g'$ as a dual $0$-form. The second derivative is, indeed, the derivative of the derivative: $$g' '=(g')'.$$
Let's find this formula in the Hodge star diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccc} g,g' '\in &C^{0}(K)& \ra{d} & C^1(K) &\\ &\ua{\star} & \ne & \da{\star} & \\ &C^{1}(K^\star)& \la{d} & C^{0}(K^\star)& \ni g' \\ \end{array} $$ If, starting with $g$ in the left upper corner, we go around this, non-commutative, square, we get: $$\star d \star dg.$$
Just as $g$ itself, its second derivative $$g' ':=\star d \star d g=(\star d)^2g$$ is another primal $0$-form.
Definition. A $0$-form $g$ is called twice differentiable if it is differentiable and so is its derivative.
Proposition. All forms are twice differentiable provided $\frac{1}{|a|}\in R$ for every cell $a$ in $K$ or $K^\star$.
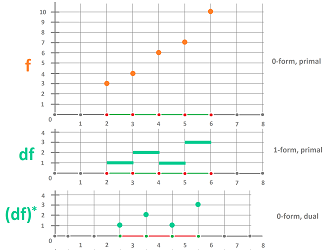
This is how the formula works in the case of edges with equal lengths:
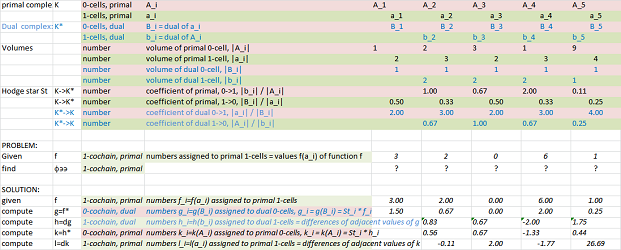
The second derivative is computed with a spreadsheet using the Hodge duality (dimension $1$):
Computing the second derivative over a geometric complex with a non-trivial geometry is slightly more complex:
Link to the file: Spreadsheets.
Exercise. Instead of a direct computation as above, implement the second derivative via the spreadsheet for the first derivative.
Proposition. If the complex $K$ is a directed graph with unit edges, the matrix $D$ of the second derivative is given by its elements indexed by ordered pairs of vertices $(u,v)$ in $K$, $$D_{uv}= \begin{cases} -1 & \text{ if } u,v \text{ are adjacent;}\\ \deg u, \text{ the degree of node }u, & \text{ if } v=u;\\ 0 & \text{ otherwise.} \end{cases}$$
Exercise. (a) Prove the formula. (b) Generalize the formula to the case of arbitrary lengths.
Exercise. Define the second derivative of a $1$-form $h$ and find its explicit formula.
Newtonian physics, the discrete version
The concepts introduced above allow us to state some elementary facts about the discrete Newtonian physics, in dimension $1$.
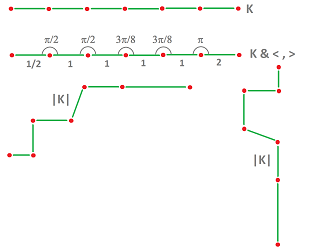
First, the time is given by the standard geometric complex $K={\mathbb R}$. Even though it is natural to assume that the complex that represents time has no curvature, it is still important to be able to have time intervals of various lengths.
Second, the space is given by our ring $R$. For all the derivatives to make sense, we may have to choose $R$ to be a field (or choose the standard geometry for time). However, even when $R={\bf R}$, there is no topology and, consequently, no assumptions are made about the continuity of the dependence on time of any of the quantities presented below.
The main quantities we are to study are:
- the location $r$ is a $0$-form;
- the displacement $dr$ is a $1$-form;
- the velocity $v=r'$ is a dual $0$-form;
- the momentum $p=mv$, where $m$ is a constant mass, is also a dual $0$-form;
- the impulse $J=dp$ is a dual $1$-form;
- the acceleration $a=r' '$ is a primal $0$-form.
These forms are seen in the following Hodge star diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{lllll} &a\ ..\ r & \ra{d}& dr &\\ &\ua{\star} & \ne & \da{\star} & \\ &J/m& \la{d} & v& \\ \end{array} $$
Newton's First Law. If the net force is zero, then the velocity $v$ of the object is constant: $$F=0 \Rightarrow v=const.$$
The law can be restated without invoking the geometry of time:
- If the net force is zero, then the displacement $dr$ of the object is constant:
$$F=0 \Rightarrow dr=const.$$ The law shows that the only possible type of motion in this force-less and distance-less space-time is uniform, i.e., it is repeated addition: $$r(t+1)=r(t)+c.$$
Newton's Second Law. The net force on an object is equal to the derivative of its momentum $p$: $$F=p'.$$
As we have seen, the second derivative is meaningless without specifying geometry, the geometry of time.
The Hodge star diagram above may be given this form: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{lllll} &F\ ..\ r & \ra{d}& dr &\\ &\ua{\star} & \ne & \da{m\star} & \\ &J\longleftarrow & \la{d} & p& \\ \end{array} $$
Newton's Third Law. If one object exerts a force $F_1$ on another object, the latter simultaneously exerts a force $F_2$ on the former, and the two forces are exactly opposite: $$F_1 = −F_2.$$
Law of Conservation of Momentum. In a system of objects that is “closed”, i.e.,
- there is no exchange of matter with its surroundings, and
- there are no external forces;
the total momentum is constant: $$p=const.$$
In other words, $$J=dp=0.$$
Indeed, consider two particles interacting with each other. By the third law, the forces between them are exactly opposite: $$F_1=-F_2.$$ By the second law, we have $$p_1'=-p_2',$$ or $$(p_1+p_2)'=0.$$
Exercise. State the equation of motion for a variable-mass system (such as a rocket). Hint: apply the second law to the entire, constant-mass system.
Exercise. Create a spreadsheet for computing all the quantities listed above.
Whatever ring we choose, even $R={\bf Z}$, the laws of physics are satisfied exactly not approximately.