This site is being phased out.
Velocity
Suppose we want to study motion. Some questions we may ask are:
- On a winding road what is the direction of the headlights?
- Where does the rock go when released from the slingshot?
The answer is to consider the tangents.
For the slingshot, we write $$f(x) = ( 1 - x^2 )^{\frac{1}{2}}$$ the graph of which is the circle. Then we differentiate and find the tangent line to the circle at any point: the slope of the tangent line is equal to the value of the derivative of $f$ at the point.
This is the way the issue is handled in Calc 1.
There are some issues though. One is that strictly speaking the circle is given by $$f(x) = \pm ( 1 - x^2 )^{\frac{1}{2}},$$ with $\pm$. So, the method only works separately for the upper and lower halves of the circle. This is where parametric curves come handy.
Define $$g(t) = ({\rm cos \hspace{3pt}} t, {\rm sin \hspace{3pt}} t), t\in[ 0, \frac{\pi}{4} ].$$
In addition to "In what direction?" we also consider "How fast?" (it's already clear that one can give one answer to both questions - in the form of a vector). Suppose it's released at time $t = \frac{\pi}{4}$. What is the velocity, with respect to $x$ and $y$, of the motion?
- $x(t) = {\rm cos \hspace{3pt}} t {\rightarrow} x'(t) = -{\rm sin \hspace{3pt}} t {\rightarrow} x'(\frac{\pi}{4}) = -\frac{1}{\sqrt{2}},$
- $y(t) = {\rm sin \hspace{3pt}} t {\rightarrow} y'(t) = {\rm cos \hspace{3pt}} t {\rightarrow} y'(\frac{\pi}{4}) = \frac{1}{\sqrt{2}}.$
Then the answer is $v = ( -\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}).$
Further, if the rock is released, it will continue with this velocity indefinitely: $$s(t) = ( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) + v( t - \frac{\pi}{4}), t \in [ \frac{\pi}{4}, \infty ),$$ where $( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})$ indicates the initial position, $v$ the velocity and $\frac{\pi}{4}$ the time since the release. This yields a straight line.
In the $n$-dimensional space, such a geometric approach is no longer valid. We have to take a more algebraic view.
Recall from Calc 1:
- Question: Given $y = f(x)$, what is the best linear approximation of $f$ around $x = a$?
- Answer: The tangent line, $g(x) = f(a) + f'(a) ( x - a ).$
Now we realize that the right term here is affine not linear.
Problem. Give the set of all affine functions passing through $(a,f(a))$ $$g(x) = f(a) + m ( x - a ).$$ which one is he best approximation of $f$ around $x = a$?
We know the answer: $m = f'(x).$
It's best but in what sense?
Let's rephrase the problem in the vector environment.
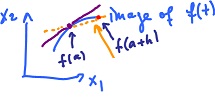
Let $f: {\bf R} {\rightarrow} {\bf R}^n, a \in {\bf R}$. What is the rate of change of $f$? We have
- $z:$ Change $f(a + h) - f(a) - f(a)$ a vector, the displacement
- $t$: Change $h$ a number, the time passed
Then the rate of change of $z$ with respect to $t$ can be expressed as $$\frac{f(a + h) - f(a)}{h}.$$ This is a vector.
The instant rate of change is $$f'(a) = \displaystyle\lim_{h \rightarrow 0} \frac{f(a + h) - f(a)}{h}.$$ Also a vector.
How can we compute this? Suppose $f(t) = ( f_1(t), f_2(t), ..., f_n(t) )$, then $$\begin{array}{} f'(a) &= \displaystyle\lim_{h \rightarrow 0} \frac{\left( f_1(a + h), ..., f_n(a + h) ) - ( f_1(a), ..., f_n(a) \right)}{h} \\ &= \left( \displaystyle\lim_{h \rightarrow 0} \frac{f_1(a + h) - f_1(a) )}{h}, ..., \displaystyle\lim_{h \rightarrow 0} \frac{f_n(a + h) - f_n(a)}{h} \right) \\ &= ( f'_1(a), ..., f'_n(a) ). \end{array}$$
So, the velocity $f'(a)$ makes sense iff the coordinate velocities $f'_i(a)$ make sense, $i = 1, ..., n$. In that case $$f'(a) = ( f'_1(a), ..., f'_n(a) ).$$