This site is being phased out.
Line integrals
Line integrals: flux
Let's review the recent integral that involved parametric curves.
Suppose $X=X(t)$ is a parametric curve on $[a,b]$. The first is the (component-wise) integral of the parametric curve: $$\int_a^bX(t)\, dt,$$ providing the displacement from the known velocity, as functions of time. The second is the arc-length integral: $$\int_C f\, dx=\int_a^bf(X(t))||X'(t)||\, dt,$$ providing the mass of a curve of variable density. The third is the line integral along an oriented curve: $$\int_C F\, dX=\int_a^bF(X(t))\cdot X'(t)\, dt,$$ providing the work of the force field. There is one more, the line integral across an oriented curve: $$\int_C F\, dX^\perp=\int_a^bF(X(t))\cdot X'(t)^\perp\, dt,$$ providing the flux of the velocity field (it is explained in this section). The main difference between the first and the rest is that the parametric curve isn't the integrand (and the output is another parametric curve) but a way to set up the domain of integration (and the output is a number).
The analysis mimics the last section. The setup is exactly the same: a vector field and a curve.
But this time the nature of the two is very different: force vs. velocity and path vs. front. We then are not after the tangent components of the vector field but after its normal components:
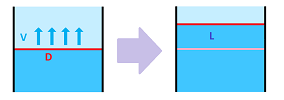
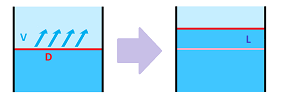
Suppose the flow with a constant speed $V$ has the front of width $D$.
Then the flux $W$ is equal to their product of these two numbers: $$L=V\cdot D.$$ The velocity may vary along this edge.
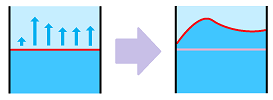
Then, as we have seen, the flux is the integral of this function: $$L=\int_D V(x)\, dx.$$
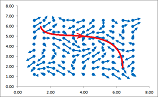
We now proceed (and will limit ourselves) to the $2$-dimensional case. We start with a constant velocity and a linear front... They may be misaligned as in the case of a wave hitting the shore:
In addition to motion “in” and “out” (as well as “left-right” and “up-down”), the third possibility emerges: what if the flow is parallel to the chosen front? Then the flux is zero. There are, of course, diagonal directions. Suppose the flow with a constant speed $V$ has the front of width $D$. Then the flux is the area swept by the progressing front:
In order to find and discard the irrelevant part of the velocity $V$, we decompose it into parallel and perpendicular components relative to $D$ just as before: $$V=V_{||}+V_\perp.$$ In contrast to the force, we pick the other component! The relevant part of the velocity $V$ is its “normal” component.
It is its projection on the direction perpendicular to the front vector: $$V_{\perp}=||V||\sin \alpha,$$ where $\alpha$ is the angle between $V$ and $D$.
This component is then multiplied by the width of the front to get the flux: $$L=V_{\perp}||D||=||V||\, ||D||\, \sin \alpha.$$
We would like to express this in terms of the dot product just as in the last section. It is the dot product of $V$ but with what vector? It is $D$ rotated $90$ degree counterclockwise: $$L=||V||\, ||D||\, \cos (\pi-\alpha).$$ Recall that the normal vector of a vector $D=<u,v>$ on the plane is given by $$D^\perp=<u,v>^\perp=<-v,u>.$$
Definition. The flux of a plane flow with velocity vector $V$ across the front vector $D$ is defined to be: $$L=V\cdot D^\perp.$$
The flux is proportional to the magnitude of the velocity and to the magnitude of the vector of representing the front.
The definition of flow applies to a straight front... or to a front made of multiple straight edges:
If these segments are given by the edge vectors $D_1,...,D_n$ and the velocity for each is given by the vectors $V_1,...,V_n$, then the flux is defined to be the simple sum of the flux across each: $$L=V_1\cdot D^\perp_1+...+V_n\cdot D^\perp_n.$$
The front above is, just as before, given by path of a parametric curve $X=X(t)$. Then, $$D_i=X(t_{i+1})- X(t_i),\ t=0,2,...,n-1.$$ Once again, it doesn't matter how fast the parametrization goes along its path. It is the front itself -- the locations and the angles relative to the flow -- that matters. This is about an oriented curve. In the mean time, the vectors of the flow come from a vector field, $V=V(X)$. In contrast to the last section, this is a velocity field. If its vectors change incrementally, one may be able to compute the flux by a simple summation, as above.
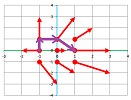
Example. In order to compute the flux of a discrete vector field across a curve made of straight edges $D_1,...,D_n$, all we need is the formula: $$L=\sum_{i=1}^nV_i\cdot D^\perp_i.$$ In order for the computation to make sense, the edges of the front and the vectors of the velocity have to be paired up! Here's a simple example:
We pick the value of the velocity from the initial point of each edge: $$L=<-1,0>\cdot <-1,0>+<0,2>\cdot <0,1>+<1,2>\cdot <-1,1>=4.$$
$\square$
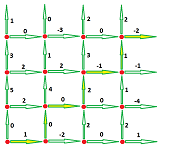
Example. An even simpler situation is when the front is made of the edges of the square grid on the plane. Then there is a velocity vector associated with each edge of the grid, but only one of its components matters: the horizontal when the edge is vertical and the vertical when the edge is horizontal. It is then sufficient to assign a single number to each edge to provide the relevant part of velocity.
Then, for example, the flux across the “staircase” is simply the sum of the values provided: $$L=1+0+0+2+(-1)+1+(-2)=1.$$
$\square$
A vector field that varies continuously from location to location or a curve that continuously changes directions will require approximations.
The general setup for defining and computing flux is identical to what we have done several times. Suppose we have a vector field $V=V(X)$ and an oriented curve $C$. We then find a regular parametrization of the latter: a parametric curve $X=X(t)$ defined on the interval $[a,b]$. We have a sampled partition $P$: $$a=t_0\le c_1\le t_1\le ... \le c_n\le t_n=b.$$ We divide the front into small segments with end-points $X_i=X(t_i)$ and then sample the velocity at the points $C_i=X(c_i)$.
Then the flux across each of these segments is approximated by the flux with the velocity constantly equal to $V(C_i)$: $$\text{ flux across }i\text{th segment}\approx \text{ velocity }\cdot \text{ length}=V(C_i)\cdot D^\perp_i.$$ Then, $$\text{total flux }\approx \sum_{i=1}^n V(X(c_i))\cdot D^\perp_i.$$ This is the formula that we have used and will continue to use for numerical approximations.
Example. Estimate the flux of the velocity field $$V(x,y)=<xy,x-y>$$ across the upper half of the unit circle directed counterclockwise. First we parametrize the curve: $$X(t)=<\cos t,\sin t>,\ 0\le t\le \pi.$$ We choose $n=4$ intervals of equal length with the left-ends as the sample points: $$\begin{array}{lll} x_0=0& x_1=\pi/4& x_2=\pi/2& x_3=3\pi/4&x_4=\pi\\ c_1=0& c_2=\pi/4& c_3=\pi/2& c_4=3\pi/4&\\ X_0=(1,0)& X_1=(\sqrt{2}/2,\sqrt{2}/2)& X_2=(0,1)& X_3=(-\sqrt{2}/2,\sqrt{2}/2)& X_4=(-1,0)\\ & D_1=(\sqrt{2}/2,\sqrt{2}/2)& D_2=(0,1)& D_3=(-\sqrt{2}/2,\sqrt{2}/2)& D_4=(-1,0)\\ & N_1=(\sqrt{2}/2,\sqrt{2}/2)& N_2=(0,1)& N_3=(-\sqrt{2}/2,\sqrt{2}/2)& N_4=(-1,0)\\ C_1=(1,0)& C_2=(\sqrt{2}/2,\sqrt{2}/2)& C_3=(0,1)& C_4=(-\sqrt{2}/2,\sqrt{2}/2)\\ V(C_1)=<0,1>& V(C_2)=<1/2,0>& V(C_3)=<0,-1>& V(C_4)=<-1/2,-\sqrt{2}> \end{array}$$ Then,... $$\begin{array}{lll} W&\approx <0,1>\cdot <\sqrt{2}/2-1,\sqrt{2}/2> + <1/2,0>\cdot <-\sqrt{2}/2,1-\sqrt{2}/2>\\ &+<0,-1>\cdot <-\sqrt{2}/2,\sqrt{2}/2-1> + <-1/2,-\sqrt{2}>\cdot <-1+\sqrt{2}/2,-\sqrt{2}/2>\\ &=.. . \end{array}$$ $\square$
Definition. Suppose $C$ is an oriented curve in ${\bf R}^2$. If a vector field $V$ in ${\bf R}^2$ is called a velocity field, then the integral, $$\int_CV\, dX^\perp=\int_a^bV(X(t))\cdot X'(t)^\perp\, dt,$$ is called the flux of the flow across the curve $C$, where $X=X(t),\ a\le t\le b$, is a regular parametrization of $C$ and $X'(t)^\perp$ is the normal of its tangent. It is also called the line integral of $V$ across $C$.
The first term in the integral shows how the velocity depends on time. Once all the vector algebra is done, this is just a familiar numerical integral from Part I.
Example. Compute the flux of a constant vector field, $V=<-1,2>$, across a straight line, the segment from $(0,0)$ to $(1,3)$. First parametrize the curve and find its derivative: $$X(t)=<1,3>t,\ 0\le t\le 1,\ \Longrightarrow\ X'(t)=<1,3>\ \Longrightarrow\ X'(t)^\perp=<-3,1>.$$ Then, $$L=\int_CV\, dX^\perp=\int_a^bV(X(t))\cdot X'(t)^\perp\, dt=\int_0^1<-1,2>\cdot <-3,1>\, dt=\int_0^1 5\, dt=5.$$ $\square$
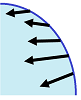
Example. Compute the flux of the radial vector field, $V(X)=X=<x,y>$, across the upper half-circle from $(1,0)$ to $(-1,0)$. First parametrize the curve and find its derivative: $$X(t)=<\cos t,\sin t >,\ 0\le t\le \pi,\ \Longrightarrow\ X'(t)=<-\sin t,\cos t>\ \Longrightarrow\ X'(t)^\perp=<-\cos t,-\sin t>.$$ Then, $$\begin{array}{lll} W&=\int_CV\, dX^\perp=\int_a^bV(X(t))\cdot X'(t)^\perp\, dt\\ &=\int_0^\pi <\cos t,\sin t >\cdot <-\cos t,-\sin t>\, dt\\ &=-\int_0^\pi 1\, dt\\ &=-\pi. \end{array}$$ $\square$
Theorem. The flux is independent of parametrization.
Theorem. $$\int_{-C}V\, dX^\perp=-\int_CV\, dX^\perp.$$
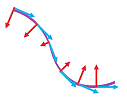
Example. Is the flux positive or negative?
More below:
$\square$
Exercise. Finish the example.
Exercise. What is the value of the line integral of the gradient of a function across one of its level curves?
Theorem (Linearity). For any two vector fields $V$ and $W$ and any two numbers $\lambda$ and $\mu$, we have: $$\int_{C}(\lambda V+\mu W)\, dX^\perp=\lambda\int_CV\, dX^\perp+\mu\int_{C}W\, dX^\perp.$$
Theorem (Additivity). For any two oriented curves $C$ and $K$ that have only finitely many points in common and together form a oriented curve $C\cup K$, we have: $$\int_{C\cup K}V\, dX^\perp=\int_CV\, dX^\perp+\int_KV\, dX^\perp.$$
To study $3$-dimensional flows, we will need to use parametric surfaces.
We can use this construction to model flows across, instead of an imaginary front, a physical barrier. Such a barrier may have a permeability that varies with location. The permeability may also depend on the direction of the flow.
Now, line integrals across closed curves.
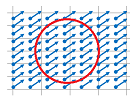
Example. What is the work of a constant vector field along a closed curve such as a circle?
Consider two diametrically opposite points. The directions of the tangents to the curve are opposite while the vector field is the same. Therefore, the terms $F\cdot N$ in the work integral are negative of each other. So, because of this symmetry, two opposite halves of the circle will have work negative of each other and cancel. The work is flux! Let's confirm this for $F=<p,q>$ and the standard parametrization of the circle: $$\begin{array}{ll} L&=\oint_CF\, dX^\perp=\int_a^bF(X(t))\cdot X'(t)^\perp\, dt\\ &=\int_0^{2\pi}<p,q>\cdot <-\sin t,\cos t>^\perp\, dt\\ &=\int_0^{2\pi}<p,q>\cdot <-\cos t,-\sin t>\, dt\\ &=\int_0^{2\pi}(-p\cos t-q\sin t)\, dt\\ &=0+0=0. \end{array}$$ There is as much water coming in as going out! $\square$
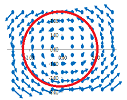
Example. The story is the exact opposite for the rotation vector field: $$F=<-y,x>.$$
Consider any point. The direction of the tangents to the curve is the same as the vector field. Therefore, flux is not zero! Let's confirm this result: $$\begin{array}{ll} L&=\oint_CF\, dX^\perp=\int_a^bF(X(t))\cdot X'(t)^\perp\, dt\\ &=\int_0^{2\pi}<-\sin t,\cos t>\cdot <-\sin t,\cos t>^\perp\, dt\\ &=\int_0^{2\pi}<-\sin t,\cos t>\cdot <-\cos t,-\sin t>\, dt\\ &=\int_0^{2\pi}(\sin t\cos t+\cos t(-\sin t))\, dt\\ &=0. \end{array}$$ No water gets in or out! $\square$