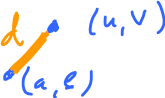Dot product

How do we compute distances and angles in vector spaces?

Plan: Take a vector space and equip it with extra structure, so that we can measure.

To understand how, let's observe that we do measure in ${\bf R}^1$, ${\bf R}^2$, ${\bf R}^3$, etc. How?

Consider the distance formula in ${\bf R}^2$.

Which is $$d=\sqrt{(a-u)^2+(b-v)^2},$$ that comes from Pythagorean Theorem.

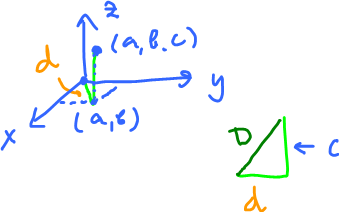
In ${\bf R}^3$ also:

we have $$D=\sqrt{(a-u)^2+(b-v)^2+(c-w)^2}$$ etc.

Then, the distance from $d=(a,b)$ to $0$ is $\sqrt{a^2+b^2}$. $$D^2=d^2+c^2 = a^2+b^2+c^2,$$ diagonal of box $a \times b \times c$.

In ${\bf R}^n$ distance formula is the following.

The distance between $a=(a_1,\ldots,a_n)$ and $b=(b_1,\ldots,b_n)$ is $$d(a,b)=\sqrt{(a_1-b_1)^2+\ldots+(a_n-b_n)^2}.$$ (it's a number!)

We can measure vectors and, therefore, can consider convergence:

• given $x_i \in {\bf R}^n$, $x_i \rightarrow a \in {\bf R}^n$ if distance from $x_i$ to $a$ goes to $0$ as $i \rightarrow \infty$, i.e.,

$$\displaystyle\lim_{i \rightarrow \infty} d(x_i,a)=0.$$

With this you can introduce limits, continuity, derivative, integral, the rest of calculus. So, we have calculus in ${\bf R}^n$ (not just ${\bf R}^3$ as in calc 3). It's called vector calculus.

Another measurement in the Euclidean space is angles.

Suppose we have $u,v \in {\bf R}^2$, so that $u=(u_1,u_2), v=(v_1,v_2)$.

Known formula: $$\cos \alpha=\frac{u_1v_1+u_2v_2}{\sqrt{u_1^2+u_2^2}\sqrt{v_1^2+v_2^2}}.$$ Here we identify the top to be the dot product of $u,v \in {\bf R}^2$ and the bottom is the norms of $u$ and $v$.

It is better notation then: $$= \frac{ < u,v > } {\lVert u \rVert \lVert v \rVert}.$$ Observation: no mention of dimension!

But does the angle between two vectors even make sense in ${\bf R}^n$?

Given $u,v \in {\bf R}^n$, what is the meaning of "the angle between vectors"?

First, we know what it is in ${\bf R}^2$.

Now, consider ${\bf R}^3$.

In ${\bf R}^3$, we make a plane $P={\rm span}\{u,v\}$ (the dimension is 2, a plane). Then we can measure the angle between these vectors -- within $P$!

Similar for ${\bf R}^n$.