Configuration spaces

Redirect to:

• Products#Configuration spaces

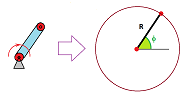
Suppose we have a robotic arm with a single joint, i.e., just a rotating rod. What is the set of all possible positions of its end? It's a circle ${\bf S}^1$ nicely parametrized by a curve, say: $$x=\cos \theta, y=0, z=\sin\theta,$$ where $\theta$ is the angle of the rod.

However, if this is a ball joint the set is a sphere ${\bf S}^2$. This sphere is also (homeomorphically) parametrized via spherical coordinates.

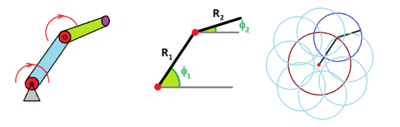
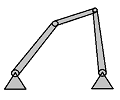
Further, the set of possible positions of a two-joint arm is more complicated:

It's either

• the disk, or
• the annulus.

Exercise. Prove that.

Its space of parameters is the torus: $${\bf T}^2={\bf S}^1 \times {\bf S}^1 .$$

This is the reason we separate the two:

• the operational space as the set of all positions reachable by a robot's end-effector in space;
• the configuration space as the set of all possible combinations of the positions of the joints.

For the two-joint arm, we could make these two homeomorphic to if we make the axes of the joints (first red, second green) perpendicular to each other with the latter shorter than the former:

This can't happen with $3$ or more joints. The reason is that there will be $n\le3,$ parameters and the space won't fit (can't be "embedded") into the Euclidean space.

In general, this setup might be much more complicated:

Exercise. Find the configuration space of this robotic arm. Hint: Don't forget the fingers!

So, the positions of the joints are used as parameters of the state of the robot.

If the motion of the joints is independent (and we ignore the possible self-intersections), the configuration space is the product of the configuration spaces of joints.

For example, a telescoping arm with a joint has the cylinder: $${\bf C}^2=[0,1] \times {\bf S}^1 $$ as the configuration space. The joint space of an $n$-joint arm (called also a "linkage") is the $n$-torus: $${\bf T}^n={\bf S}^1 \times ... \times {\bf S}^1 .$$ Also, even if the arm has delivered the end-effector to its intended location, the task at hand, such as spray-painting, may require a particular direction. This would add an extra term $\times {\bf S}^2$.

These examples suggest that configuration spaces should be manifolds.

Exercise. What is the configuration space of a pendulum attached to a spring?

Exercise. What is the configuration space of the three-joint arm the end of which is fixed? Hint: The answer will depend on the relative lengths of the rods.

The robot's forward and inverse kinematics equations define functions from its configuration space to the operational space. These functions are then used for motion planning.

In physics, an example of a configuration space is the state space of $n$ particles. In the simplest setting, it's $$C=({\bf R}^3)^n.$$ Every configuration corresponds to a single point in this space.

The answer changes, however, if we drop the implicit assumption that the particles are distinguishable. In that case, the configuration space is $$C=({\bf R}^3)^n/_{\sim},$$ where $\sim$ is an equivalence relation derived from the identification of each pair of particles.

Exercise. What is the configuration space of two and three particle systems with identical particles?

Another issue is, can two particles occupy the same location? If the answer is No, we have to exclude the "diagonals" from the configuration space: $$C=({\bf R}^3)^n -D,$$ where $$D=\{(u_1,...,u_n)\in ({\bf R}^3)^n: \exists i \ne j,u_i = u_j\}.$$

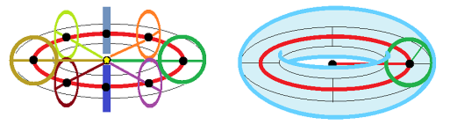
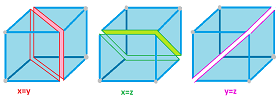
This idea is applied for "collision avoidance" in robotics by constructing such a "safe" configuration space. On a line segment, this configuration space of three robots will be a cube with three planes cut out:

Exercise. How many connected components does this space have?

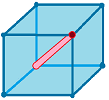
If two can pass each other (but not three), the configuration space is a cube with the diagonal drilled out:

It is connected!

Exercise. Find the safe configuration space for two robots on a line, the circle, the tripod. What if they are connected by a rod? a rope?

In general, if the motion is within manifold $M$ of dimension $m$, then the configuration space is also a manifold but of dimension $mn$.

If molecular bonds are present, things are more complicated. Suppose, for example, we have two atoms in space. Then their configuration space is $({\bf R}^3)^2$. Now suppose this is a two-atom molecule with two (different) atoms. Then its state is described, independently, by

• the location of its center of mass (or either of the two atoms as a point of reference) and
• the orientation of one of the atoms with respect to that point (the distance is fixed).

Therefore, the configuration space is ${\bf R}^3 \times {\bf S}^2$.

Exercise. What if this is a two-atom molecule with two identical atoms?

One can also take into account the velocity (or momenta) of each particle. Then one considers the values in the tangent bundle $TM$ of $M$. In fact, the cotangent bundle $T^{*}M$ of $M$ can be thought of as the set of possible positions and momenta. The totality is called the phase space of the system. Example: the phase space of a pendulum is the cylinder.